WALL EFFECTS ON FLOWS PAST TWO TANDEM CYLINDERS OF DIFFERENT DIAMETERS*

JIANG Ren-jie

State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China, E-mail: Jiangrenjie2006@126.com

LIN Jian-zhong

China Jiliang University, Hangzhou 310018, China

State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China

WALL EFFECTS ON FLOWS PAST TWO TANDEM CYLINDERS OF DIFFERENT DIAMETERS*

JIANG Ren-jie

State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China, E-mail: Jiangrenjie2006@126.com

LIN Jian-zhong

China Jiliang University, Hangzhou 310018, China

State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China

(Received October 15, 2011, Revised December 12, 2011)

Flows past two tandem cylinders of different diameters placed centrally in a channel with fixed centre-to-centre spacing 6D and diameter ratio γ=1.5are simulated based on the Lattice Boltzmann Method (LBM). In all the simulations, the diameter of the smaller cylinder is chosen as the characteristic length. The Reynolds number based on the average inflow velocity is 20-120 and studies are over the range of blockage ratio 2-8. In both Small-Big Arrangement (SBA) and Big-Small Arrangement (BSA), the effects of the channel width and Reynolds number on the flow structures and force coefficients are studied. Results show that the flows in BSA are more regular than those in SBA for the same flow fields. In BSA with 4D≤H≤8D and Re=100, the force coefficients all fluctuate with constant amplitudes and a coupled frequency, the coupled frequency becomes small as the blockage ratio decreases and by an exact test we give out the relation of the blockage ratio and Strouhal number. As the blockage ratio decreases to 2, there exist pitchfork bifurcations in both SBA and BSA, and results show that the critical Reynolds numbers of pitchfork bifurcations for SBA and BSA are both between 60 and 80. In SBA with Re=80, the flow structure has a static asymmetric mode. It is found that the channel width has also an effect on the critical spacing where the flow changes from single body mode into co-shedding mode. By an accurate survey on flows past two cylinders with equal diameters placed inside a channel with the width, the relation between channel width and the critical spacing is given and results show that the critical spacing increases as the channel width increases.

two tandem cylinders, different diameters, blockage ratio, critical spacing, Lattice Boltzmann Method (LBM)

Introduction

Flows past one or more bluff bodies exist universally in nature and can be found in many engineering applications, such as power lines, bridge piers, and off-shore engineering structures. Because of the geometric simplicity and complicated mechanism, flow past a circular cylinder has become a major topic in fluid mechanics and the fruitful results are summarised by several comprehensive reviews[1].

Effort has been made by several researchers to investigate the flow past circular cylinders of identical diameters with a variety of arrangements[2-6]. Broadly speaking, these studies have shown that the arrangements and spacings of cylinders have a significant effect on the flow structures and the force coefficients. Flows past two tandem cylinders of identical diameters are classified into several regimes and in the co-shedding regime, the two cylinders shed vortices separately at the same frequencies.

Meneghini et al.[3]studied the effect of the spacing of two cylinders for both the tandem arrangement and the side by side arrangement. For the tandem arrangement, a negative drag force on the downstream cylinder was observed for the centre-to-centre spacing smaller than 4D and a positive drag force for spacing greater than 4D. For values of spacings between two cylinders 3SD≤ vortices are shed only fromthe downstream cylinder and for values of 4SD≥vortices are shed from both bodies. Sharman et al.[4] also pointed out that the flow patterns could be divided into two regimes by a critical spacing between 3.75D and 4D atRe =100.

Flows past cylinders of different diameters are more complicated than the situations of the equal diameters, and there is little information in the literature on the flows past cylinders of different diameters. Zhao et al.[7] studied viscous flow past two cylinders of different diameters with the finite element method. The diameter ratio is 0.25 and Re=500. The gap between the two cylinders ranges from 0.05 to 1.0 times the diameter of the larger cylinder. The position angle α of the small cylinder relative to the flow direction ranges from 0 to π. Their results showed that for the position angle of the smaller cylinder α form 0.125π and 0.875π, the shedding flow behind the two cylinders can be classified into three types. The time-averaged mean drag forces on the large and the small cylinders attain the maximum values as α is around /2π. Vortex shedding frequency for the large cylinder is generally smaller than that of a single cylinder at the same Reynolds number. Alam and Zhou[8] experimentally researched the flow past two tandem cylinders of different diameters. The diameter of the downstream cylinder D was fixed at 0.025 m and the diameter of upstream cylinder d varied from 0.24-1DD. The spacing between cylinders was 5.5d. Two frequencies were detected behind the two cylinders, including the case of /=1d D, but only one dominant frequency occurred. As /d D decreased, the time-averaged drag on the downstream cylinder increases and the width of the wake between the cylinders appeared to become narrow.

Investigations of flow over a cylinder placed in a parallel channel show that the channel wall has a significant effect on the flow pattern and the force coefficients[9-12]. Chakraborty et al.[9] numerically researched the flow past a circular cylinder in a plane channel for blockage ratio λ between 1.54 and 20 and Re between 0.1 and 200. Their results showed that the drag coefficient decreases with an increase of Re and λ. Both the length of the recirculation zone and the angle of separation were found to increase with an increment of Re for a fixed value of λ due to the separation of boundary layer at higher Reynolds number. Rehimi et al.[10] studied the effects of wall confinement on stability and wake formation for flow over a circular cylinder by PIV measurements. Studies over the range of Re=30-277 with blockage ratio of 1/3 showed that wall confinement delays instability at Re=108 and three-dimensional spanwise instabilities are observed at the higher Reynolds number. Singha and Sinhamahapatra[11] used an unstructured grid, finite volume collocated Navier-Stokes solver to simulate the flows past a circular cylinder placed symmetrically in a channel with Reynolds numbers from 45 to 250 and with the blockage ratio varying from 2.0 to 8.0. Wall proximity was found to have a considerable influence on the location of the separation points and length of the closed recirculating zones. The separation points were found to move rearward, resulting in a shorter wake with decreasing channel height. The presence of the sidewalls also delays the transition from a steady flow with closed attached wake to an unsteady flow. Huang and Sworn[13]carried out the analysis of model test results to study the hydrodynamic interaction between a pair of elastically-supported rigid cylinders of dissimilar diameters in water flume. It was found that the lift on and the cross-flow motion of the downstream cylinder have the frequency components derived from the upstream cylinder’s vortex shedding as well as from its own vortex shedding.

In this article, we numerically investigate the wall effects on the flows past two tandem cylinders of different diameters with the Lattice Boltzmann Method (LBM). Our main interest focuses on the effects of channel walls and arrangements on the flow field, force coefficients and the critical spacings where flows change from single body modes to co-shedding modes. For the two tandem cylinders with different diameters, there are two different symmetrical arrangements, and the differences of flow behaviors between the two arrangements named Small-Big Arrangemen (SBA) and Big-Small Arrangement (BSA) are studied.

Fig.1 Schematic diagram of the flow

1. Problem statement and numerical method

1.1 Problem statement

Figure 1 presents the schematic diagram of the flow past two tandem cylinders of different diameters placed centrally inside a channel.1D and2D are diameters of upstream cylinder and downstream cylinder, respectively. S is the centre-to-centre cylinder spacing of two cylinders. To keep all the simulations unified, the nondimensional diameter of the smaller cylindersmall=1DD is chosen as the characteristiclength for all the simulations in this article. H and L are the width and length of the channel, respectively, and blockage ratio λ=H/ D ranges from 2 to 8. The inlet boundary is 6D upstream of the upstream cylinder centre and the velocity sensing point P where recorded velocity history is 3D downstream of the centre of the downstream cylinder at the centerline. The diameter ratio γ=Dbig/Dsmallis fixed at 1.5 for both SBA (the diameter of the upstream cylinder is smaller than the downstream one) and BSA (the diameter of the upstream cylinder is bigger than the downstream one).

An incompressible Newtonian fluid is considered, and the inlet flow velocity is given by a prescribed parabolic profile

where Umaxis the centerline velocity. The Reynolds number is defined by the average inflow velocity U=2Umax/3, i.e., Re=UD/ν and in the present study Re=20-120.

The drag coefficient CDand the lift coefficient CLare defined as

wherexF andyF represent horizontal force and vertical force, respectively, ρ is the fluid density, D is the cylinder diameter and the subscript (=i 1,2), represent upstream cylinder and downstream cylinder, respectively.

The Strouhal number is defined as

wheresf is the vortex shedding frequency.

1.2 Lattice Boltzmann Method

The LBM has been a promising numerical tool to effectively model complex physics in computational fluid dynamics. The fundamental idea of LBM is to construct simplified kinetic models that incorporate the essential physics of microscopic or mesoscopic processes so that the macroscopic averaged properties obey the desired macroscopic equations. The original lattice Boltzmann equation in the discrete microscopic velocity space is given as

whereif is the density distribution function,ie is the streaming velocity in the ith direction in the phase space, =0,1,iN… andiΩ is the collision operator and the Bhatager-Gross-Krook collision term, given as

gle relaxation time, and for the square lattice, the equilibrium function is taken as[14]

where ρ and u are the macroscopic fluid density and velocity, respectively, and =/cxtΔΔ is the lattice speed.

By the multi-scaling expansion[14]and in the limit of long wavelengths, the lattice Boltzmann equation recovers the following quasi-incompressible Navier-Stokes equations:

The two-dimensional-nine-speed model is chosen in this study. The two-dimensional velocity in the phase space is discretized into nine directions

An extrapolation method[15]for curved walls is adopted in the present simulation. This treatment has been proved to be of second-order accuracy, and has well-behaved stability characteristics.

Fig.2 Flows past a circular cylinder at =100Re

Table 1 CD, CLand St for the flow past a cylinder in an unbounded domain at Re=100

2. Validation of the algorithm

Flows past a circular cylinder immersed in a free stream have been researched by many scholars[1], the conclusions are relatively matured and such a topic is usually selected as the validation of numerical methods.

Fig.3 Instantaneous vorticity contours of flows past two cylinders with different diameters at =100Re

The flow past a circular cylinder at Re=100 is simulated with mesh density D/δx=40 and 60, where δx is the length of lattice, the dimensionless free-stream velocity U=0.1 and simulation domain L× H=48 D×2 4D. The cylinder centr e is plac ed at thecentrelineand 12D downstreamoftheinletboundary. Figure 2 shows the instantaneous pressure and vorticity contours, time evolution of CDand CL. Table 1 shows the present results of CD, CLand St. The present results agree well with previous results and a finer mesh with D/δx=60 and average velocity U=0.05 is adopted in the next study.

Fig.4 Time evolution of drag coefficients and lift coefficients in the flows past two cylinders with different diameters at =100Re

3. Results and discussion

3.1 Flows past two cylinders with different diameters placed inside a channel

3.1.1 Wall effects on flows past two cylinders with different diameters

Fig.5 Velocity phase portrait plots of flows past two cylinders with different diameters at =100Re

In this section, we investigate the effect of the blockage ratio to the force coefficients and flow structure with Re=100. The blockage ratio is between 2 and 8 and the diameter ratio is fixed at 1.5 for both arrangements. The instantaneous vorticity contours, force coefficients and velocity phase portrait plots are shown in Figs.3-5. In the SBA with H=4D and H=6D as shown in Figs.3(a) and 3(b), vortices shed from both the upstream cylinder and the downstream cylinder, the flow structure of =4HD is regular but of =6HD is irregular. In Figs.4(a) and 5(b), the drag and lift coefficients of both cylinders in a channel with =4HD fluctuate with constant amplitudes and a coupled frequency and the velocity phase portrait plot is shown as a closed curve. In Figs.4 (b) and 5 (c), the drag and lift coefficients ofSBA with H=6D fluctuate with unequal amplitudes and velocity phase portrait plot shows that the wake flow is quasi-periodic. Figure 6 shows the velocity phase portrait plots of H=6D, Re=60 and H=4D, Re=120 and results show that the flow of H=6D, Re=60 is regular but the flow of H= 4D, Re=120 turns to be non-periodic. As a conclusion, the critical Reynolds numbers where periodic behavior disappear in the flows past two cylinders in SBA are 100-120 for channel width 4D and 60-100 for channel width 6D, respectively. As is shown in Figs.3(c) and 5(d), when the channel width is H= 8D, the vortices only shed from the downstream cylinder. Such a phenomenon means that the channel width also has an effect on the critical spacing where flow changes from single body mode to co-shedding mode and the force coefficients have acute change. In the final part we will give an accurate numerical measure of the relation between the channel width and the critical spacing.

Fig.6 Velocity phase maps of flows past two cylinders with different diameters in a channel

The results of flow behaviors in the BSA with H=4D, 6D and 8D are summarized in Figs.3(d), 3(e), 3(f) and 4(c), 4(d), in all the three situations vortices shed from both cylinders, the flow structures are regular and the drag and lift coefficients of both cylinders fluctuate with constant amplitudes at a coupled frequency. In Figs.5(f), 5(g) and 5(h), we can see that the corresponding velocity phase portrait plots are all shown as closed curves. As the blockage ratio increases, the average drag coefficients of both two cylinders decreases, the fluctuation amplitudes of lift coefficients increase and the coupled vortex shedding frequency decreases. Figure 7 shows the relation of γ and St, it can be seen that St decreases as the γ increases.

Fig.7 Relation of blockage ratio and Strouhal number at Re=100, BSA

3.1.2 The critical Reynolds numbers where pitchfork bifurcations happen

For both SBA and BSA with Re=100 with H=2D, pitch-fork bifurcations happen in the flows, the flow structures are asymmetric to time and space, the average lift coefficients are not zero any more, and the deviations are even more obvious for the bigger cylinders. By investigating the behaviors of flows past one cylinder placed inside a channel with similar low blockage ratio, Sahin and Owens[12]also gave such a pitchfork bifurcation. In the following, we try to do a further investigation on flows over such systems with the Reynolds numbers between 20 and 100. Our main purpose is to find out critical Re where pitchfork bifurcations happen and part of the results are shown in Figs.8-9. In Figs.8(a) and 8(c), as =60Re, the time average lift coefficients are zero for both arrangements, which means that no pitchfork bifurcation happens in the corresponding flows. In the SBA, as shown in Fig.8(a), the flow is steady and the time evolution lift coefficients of both cylinders have no fluctuation. In the BSA, as shown in Fig.8(c), vortices shed from both two cylinders and the lift coefficients of two cylinders fluctuate with constant amplitudes and a coupled frequency. In Figs.8(b) and 8(d) we can see in both the SBA and BSA with =80Re, after sufficient time steps, there are deviations from the centerlines in the time evolution lift coefficients, which means that pitchfork bifurcations happen. In the SBA, the lift coefficients of both cylinders still keep a constant value after the pitchfork bifurcation, similarly, the vortex structure is steady and asymmetric, see Fig.9(a), and as =100Re, the steady flow structure loses the stability and vortex streets appear. In the BSA, before the pitchfork bifurcation, vortices shed from the downstream cylinder (see Fig.9(b)) and thelift coefficients of two cylinders fluctuate asymmetrically with constant amplitudes (see Fig.8(d)). After the bifurcation, the lift coefficients still fluctuate with constant amplitudes and a coupled frequency, but have obvious deviations from the centerlines. From the foregoing, critical Reynolds numbers where pitchfork bifurcations happen are between 60 and 80 for both SBA and BSA, and because the big cylinders act the leading roles in these bifurcations, the asymmetry of flow structures behind the big cylinders are more prominent and the deviations of force coefficients are also more than the small cylinders.

Fig.8 Time evolution of lift coefficients in the flows past two cylinders with different diameters in a channel with H=2

Fig.9 Instantaneous vorticity contours of flows past two cylinders with different diameters in a channel with =2H

Table 2 Relation of critical spacing and wall width at Re=100

3.2 Relation between critical spacing and channel wall width

As we have shown in Fig.3, when flows past two cylinders of different diameters in SBA placed inside a channel with =8HD, vortices only shed behind the downstream cylinder. In other situations vortices shed behind both two cylinders, which means that the wall width also has an effect to the critical spacing where flow structure changes from one single body mode into co-shedding mode. In this section, we investigate the relation of critical spacing and wall width between 2D and 8D. For convenience, the diameters of two cylinders are equal in this section and the Reynolds number is confined to 100. For the spacing between two cylinders near the critical spacings, the flow mode transformation usually appears after long simulation time steps, so balancing the numerical accuracy and the computation time, in this section the mesh with D/δx=40 and U=0.08 is used to get the exact critical spacings. As a comparison, all thesituations are also simulated by the mesh with D/ δx=24 and U=0.1, and for all the wall widths, the difference of critical spacings between the coarse mesh and the fine mesh are all smaller than 0.02D. The results from the fine mesh are summarized in Table 2. For an example, Fig.10 shows the vortex structures of the situation of =4HD with =S 3.92D and 3.96D, respectively. Figure 11 shows the relation between channel width and critical spacing and results show that the critical spacing increases as the wall width increases, which means that the wall have a significant effect on the flow mode transformation. The mechanization of such a phenomenon is that when the channel is narrow, the walls have a strong extrusion to the flows, and such an extrusion induces that the formative vortices pair behind the upstream cylinder shed early and need smaller spacing between two cylinders.

Fig.10 Instantaneous vorticity contours of flows past two cylinders with equal diameters in a channel with =4H and =100Re

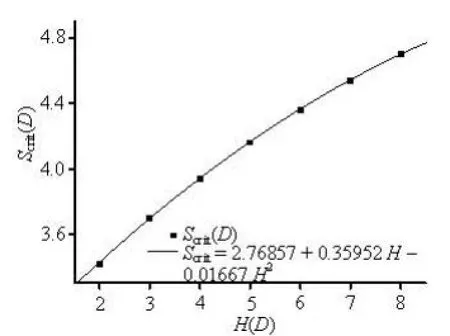
Fig.11 Relation of critical spacing and wall width at =100Re

4. Conclusions

Flows past two tandem cylinders of diameter ratio γ=1.5in both the SBA and BSA have been simulated with the LBM. For both arrangements, simulations are over the range of blockage ratio 2-8 and Re=20-120. The main conclusions are summarized as follows:

(1) Through researching the flows past two cylinders of different diameters in a channel with blockage ratio 2≤λ≤8, we find that the channel walls have a modulation effect on the flow structures and force coefficients in both the SBA and BSA. When the channel width is between 4D and 8D, the modulation effect becomes more significant as the channel width decreases. In the BSA with Re=100 and 4D≤H≤8D, the flow structures and fluctuations of force coefficients are all regular. The relation between St and γ is also given and results show that St decreases as γ increases.

(2) As the channel width is 2D, beyond the Hopf bifurcations, there are also pitchfork bifurcations in both two arrangements and the critical Reynolds numbers of the pitchfork bifurcations for the SBA and BSA are both between 60 and 80. For the Reynolds number above the critical values, the vortex structures become asymmetric and the average lift coefficients of the both cylinder is no longer zero.

(3) The channel wall has effect on the critical spacings where the flows change from one single body modes to co-shedding modes and the force coefficients have acute changes. By an accurate survey of flows past two cylinders with identical diameters in channels with Re=100 and 2D≤H≤8D, we get the relation of the critical spacing and channel width and result shows that the critical spacing increases as the channel width increases.

[1] NORBERG C. Fluctuating lift on a circular cylinder: Review and new measurements[J]. Journal of Fluids and Structures, 2003, 17(1): 57-96.

[2] DENG Jian, REN An-lu and ZOU Jian-feng. Threedimensional flow around two tandem circular cylinders with various spacings at Re=200[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(1): 48-54.

[3] MENEGHINI J. R., SALTARA F. and SIQUEIRA C. L. R. et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-byside arrangements[J]. Journal of Fluids and Structu- res, 2001, 15(2): 327-350.

[4] SHARMAN B., LIEN F. S. and DAVIDSON L. et al. Numerical predictions of low Reynolds number flows over two tandem circular cylinders[J]. International Journal for Numerical Methods in Fluids, 2005, 47(5): 423-447.

[5] GHADIRI-DEHKORDI Behzad, SARVGHADMOGHADDAM Hesam and HOURI JAFARI Hamed. Numerical simulation of flow over two circular cylinders in tandem arrangement[J]. Journal of Hydrodynamics, 2011, 23(1): 114-126.

[6] GUO Xiao-hui, LIN Jian-zhong and TU Cheng-xu et al. Flow past two rotating circular cylinders in a side by side arrangement[J]. Journal of Hydrodynamics, 2009, 21(2): 143-151.

[7] ZHAO M., CHENG L. and TENG B. et al. Numerical simulation of viscous flow past two circular cylinders of different diameters[J]. Applied Ocean Research, 2005, 27(1): 39-55.

[8] ALAM M. M., ZHOU Y. Strouhal numbers, forces and flow structures around two tandem cylinders of different diameters[J]. Journal of Fluids and Structures, 2008, 24(4): 505-526.

[9] CHAKRABORTY J., VERMA N. and CHHABRA R. P. Wall effects in flow past a circular cylinder in a plane channel: A numerical study[J]. Chemical Engineering and Processing, 2004, 43(12): 1529-1537.

[10] REHIMI F., ALOUI F. and BEN NASRALLAH S. et al. Experimental investigation of a confined flow downstream of a circular cylinder centred between two parallel walls[J]. Journal of Fluids and Structures, 2008, 24(6): 855-882.

[11] SINGHA S., SINHAMAHAPATRA K. P. Flow past a circular cylinder between parallel walls at low Reynolds numbers[J]. Ocean Engineering, 2010, 37(8-9): 757-769.

[12] SAHIN M., OWENS R. G. A numerical investigation of the wall effects up to high blockage ratios on twodimensional flow past a confined circular cylinder[J]. Physics of Fluids, 2004, 16(5): 1305-1320.

[13] HUANG Shan and SWORN A. Some observations of two interfering VIV circular cylinders of unequal diameters in tandem[J]. Journal of Hydrodynamics, 2011, 23(5): 535-543.

[14] CHEN S., DOOLEN G. D. Lattice Boltzmann method for fluid flows[J]. Annual Review of Fluid Mechanics, 1998, 30: 329-364.

[15] GUO Z. L., ZHENG C. G. and SHI B. C. An extrapolation method for boundary conditions in lattice Boltzmann method[J]. Physics of Fluids, 2002, 14(6): 2007-2010.

[16] PARK J., KWON K. and CHOI H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J]. KSME International Journal, 1998, 12(6): 1200-1205.

10.1016/S1001-6058(11)60212-6

* Project supported by the Major Program of the National Natural Science Foundation of China (Grant No.11132008).

Biography: JIANG Ren-jie (1982-), Male, Ph. D Candidate

LIN Jian-zhong,

E-mail: mecjzlin@public.zju.edu.cn

2012,24(1):1-10