一类二阶多时滞泛函微分方程多个周期解的存在性
2012-05-11于跃华贾仁伟黄祖达
于跃华, 贾仁伟, 黄祖达
一类二阶多时滞泛函微分方程多个周期解的存在性
于跃华, 贾仁伟, 黄祖达
(湖南文理学院 数学与计算科学学院,湖南 常德, 415000)
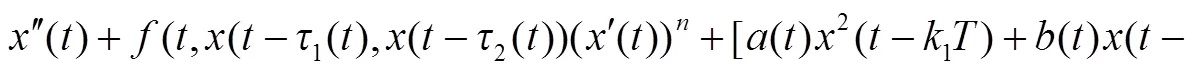
泛函微分方程; 重合度; 多个周期解
泛函微分方程周期解的存在性问题一直是人们广泛研究的课题. 近年来, Mawhin的重合度理论延拓定理已成为研究周期解存在性问题的强有力工具[1-5], 文献[6]利用这种方法研究了另一类二阶非线性泛函微分方程多个周期解的存在性, 但在证明过程中还存在一些不够完善的地方, 本文考虑如下一类多时滞二阶泛函微分方程:

为了行文方便, 引入Mawhin的重合度理论[7], 设,为Banach空间,: dom为指标为零的Fredholm算子,为连续投影, 满足: Im=Ker, Im=Ker,. 定义的广义逆为因为同构, 记同构映射为
则方程(1)至少有两个-周期解.
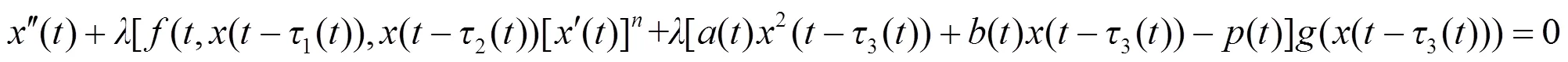



于是由式(3)、(4)知:

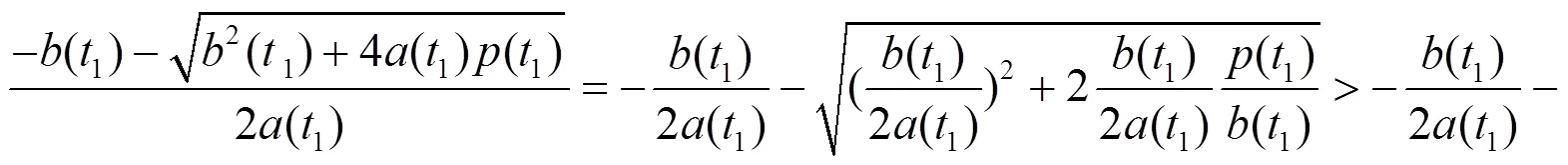

从而可得:

由式(5)和(6)可得:

或者


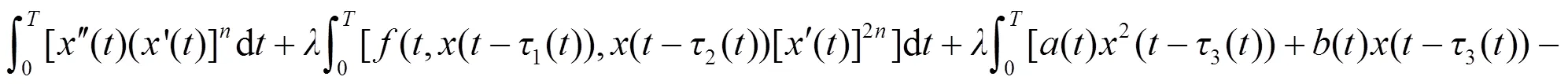
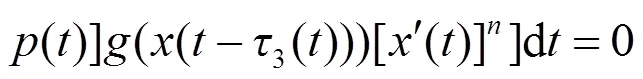
由此得:
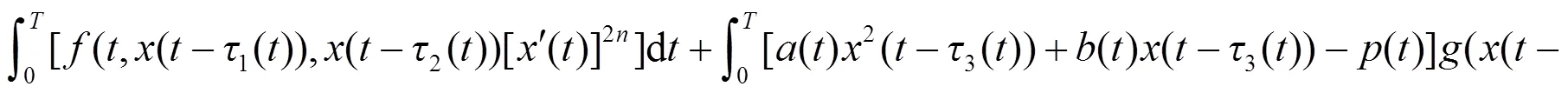




从而有:
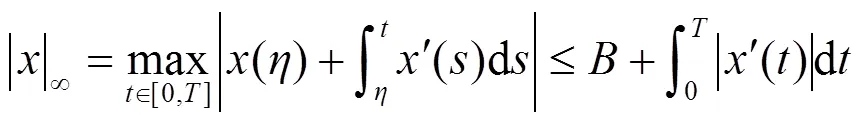

于是:




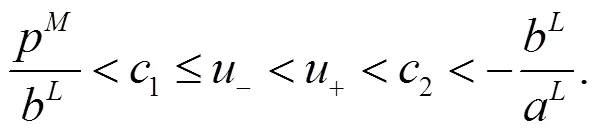

即:
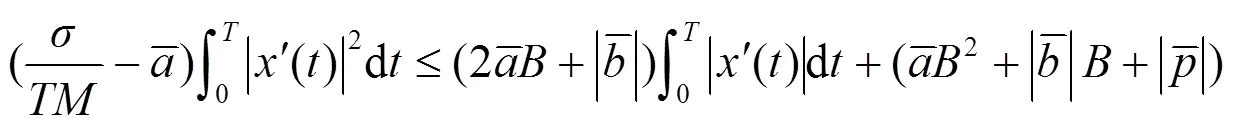
[1] Lu S, Ge W. Periodic solutions for a kind of second order differential equation with multiple deviating argument[J]. Appl Math Comput, 2003, 146: 195-209.
[2] Huang C, He Y, Huang L, et al. New result on the periodic solutions for a kind of Rayleigh equation with two deviating argu- ments[J]. J Math & Comput Modell, 2007, 46: 604-611.
[3] Peng L, Liu B, Zhou Q, et al. Periodic solutions for a kind of Rayleigh equation with two deviating arguments[J]. J Franklin Inst, 2006, 7: 676-687 .
[4] Sırma A, Tunç C, Özlem S. Existence and uniqueness of periodic solutions for a kind of Rayleigh equation with nitely many deviating arguments[J]. Nonlinear Analysis, 2010, 73(2): 358-366.
[5] Burton T A. Stability and Periodic Solutions of Ordinary and Functional Differential Equations[M]. Orlando: Academic Press, 1985.
[6] 田德生, 曾宪武. 一类二阶泛函微分方程多个周期解的存在性[J]. 数学物理学报, 2010, 30A(2): 525-530.
[7] Gains R E, Mauhin JL. Coincidence Degree and Nonlinear Differential Equations[M]. Berlin: Springer, 1977.
On existence of serveral periodic solution for a class of second order multi-delay functional diferential equations
YU Yue-hua, JIA Ren-wei, HUANG Zu-da
(Department of Maths and Computing, Hnnan University of Arts and Science, Changde 415000, China)
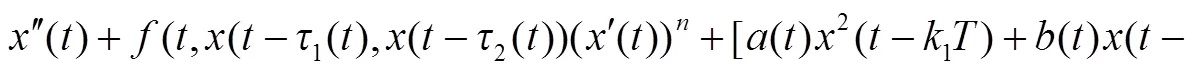
Functional differential equations; mult-periodic solutions; coincidence degree
10.3969/j.issn.1672-6146.2012.03.001
O 175.6
1672-6146(2012)03-0001-05
2012-08-30
湖南省教育厅资助课题2010[243], 湖南文理学院芙蓉学院2010-2011重点课题资助
于跃华(1971-), 女, 副教授, 研究方向为微分方程. E-mail: 2424676032@qq.com
(责任编校: 刘晓霞)
