简支梁桥顺桥向固有振动

王振湘



简支梁桥顺桥向固有振动

王振湘

(湖南常德公路工程总公司, 湖南 常德, 415000)

考虑简支梁桥顺桥向振动特点, 建立了固有振动模型: 将桥墩简化为悬臂梁, 在墩顶处采用弹簧模拟板式橡胶支座, 上部结构简化为集中质量, 基于贝努利——欧拉梁振动理论和达朗伯原理, 考虑轴向力对简支梁桥顺桥向固有振动影响, 得到了简支梁桥顺桥向固有振动的解析式.

简支梁桥; 固有振动; 频率; 贝努利——欧拉梁

简支梁桥是一种静定结构, 结构内力不受地基变形, 温度改变的影响, 是目前我国广泛使用的一种桥梁结构形式. 其构造简单, 施工方便, 主要由上部结构、支座系统、桥墩、桥台和墩台基础等组成. 简支梁桥承受车辆荷载、地震荷载等动荷载时, 桥梁将发生振动. 国内外桥梁地震震害调查表明, 多跨梁桥的顺桥向地震震害较为严重[1], 因此研究简支梁桥顺桥向固有振动对简支梁桥的动力特性具有重要意义. 文献[2]研究了车流作用下简支桥梁的随机振动;文献[3]研究了弹性地基上连续梁桥顺桥向地震振动;文献[4]研究了多片梁组成的简支梁桥车桥耦合振动响应.这些研究得到了一些重要的研究成果, 对于研究桥梁动力特性具有重要的参考价值, 但这些研究的求解体系过于繁琐, 且没有考虑轴向力对桥梁振动的影响.

本文考虑简支梁桥顺桥向振动特点, 提出了适用于该体系的动力特性的解析公式, 并分析了相关参数对简支梁桥顺桥向固有振动特性的影响. 由于简支梁桥中上部结构质量所占比重较大, 墩中轴力会对结构频率产生一定影响, 所以在解析法中考虑了轴力对体系频率的影响.

1 简支梁桥顺桥向固有振动模型

研究表明, 简支梁桥顺桥向固有振动具有如下特点[5]: 上部结构质量、桥墩质量和桥墩刚度以及支座刚度对顺桥向固有振动特性影响较为显著, 而主梁的刚度则影响不大. 考虑简支梁桥顺桥向振动特点, 将简支梁桥墩简化为悬臂梁, 悬臂梁抗弯刚度, 单位长度质量, 跨长, 墩顶处板式橡胶支座采用弹簧模拟, 弹簧刚度取为板式橡胶支座本身的剪切刚度. 不考虑简支梁桥上部结构的刚度, 将其简化为集中质量, 在墩顶通过弹簧与悬臂梁相连. 简支梁桥顺桥向固有振动模型及坐标系如图1所示.

图1 简支梁桥顺桥向固有振动模型

2 简支梁桥顺桥向固有振动解析解

桥墩简化为悬臂梁, 暂不考虑轴力影响, 以弯曲变形为主的悬臂梁的静力平衡微分方程为:

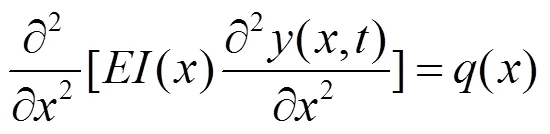
根据达朗伯原理, 上部结构动力方程为:

设式(4)、式(5)的解分别为:

将式(6)代入式(5)可得:

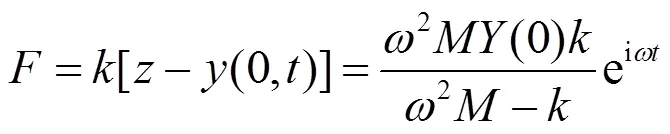
结合式(4)、(6)可得:

将边界条件式(9)、(10)代入式(11), 可以得到关于结构自振频率的特征方程:

式(13)即为不考虑轴力影响时的简支梁桥顺桥向固有振动解析解.

3 轴力对简支梁桥顺桥向固有振动的影响

考虑轴力影响, 其计算模型同样如图1所示. 此时, 上部结构的动力方程没有变化, 即式(5). 桥墩结构在轴力作用下, 弯曲振动的振型曲线的微分方程为:

同理, 设式(14)的解为:

将式(15)代入式(14), 可得:

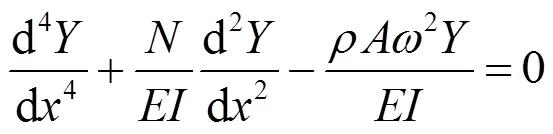
求解式(16), 有:

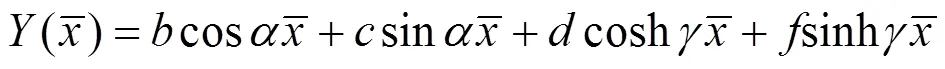
其边界条件仍然是式(9)、(10), 将边界条件代入式(17)可以得到关于结构自振频率的特征方程:

4 算例分析

由表1可以看出, 无论是否考虑轴力影响, 当支座刚度与简支梁桥下部结构刚度比不变时, 随着上部质量与下部质量比的增大, 结构顺桥向振动频率变小, 且对第一阶自振频率影响较大, 对高阶自振频率影响较小.究其原因是简支梁桥顺桥向固有振动一阶振型是上部集中质量、支座和桥墩的耦合振动, 其中集中质量的振动占优, 而在高阶振型中上部结构自身振动比较重要. 当上部质量与下部质量比不变时, 随着支座刚度与下部结构刚度比的增大, 结构顺桥向振动频率变大, 这是因为增大时, 结构刚度变大. 考虑轴力影响后, 简支梁桥顺桥向固有振动频率降低.

表1 不考虑轴力和考虑轴力时简支梁桥顺桥向固有振动前三阶频率

5 结论

简支梁桥固有振动的研究是简支梁桥抗震设计和健康状态检测的基础. 基此本文考虑简支梁桥顺桥向振动特点, 提出了悬臂梁顶部用弹簧联接集中质量的计算模型, 给出了不考虑和考虑轴力影响的简支梁桥体系频率的解析公式. 利用该解析式研究简支梁桥顺桥向固有振动, 计算简单, 应用方便.

无论是否考虑轴力影响, 当支座刚度与下部结构刚度比不变时, 随着简支梁桥上部质量与简支梁桥下部质量比的增大, 结构顺桥向振动频率变小, 且对第一阶自振频率影响较大, 对高阶自振频率影响较小. 当上部质量与下部质量比不变时, 随着支座刚度与下部结构刚度比的增大, 结构顺桥向振动频率变大. 考虑轴力影响后, 简支梁桥顺桥向固有振动频率降低.

[1] 周勇军, 彭晓彬, 赵煜, 等. 简支梁桥顺桥向地震动分析[J]. 交通运输工程学报, 2007, 7(6): 86-89.

[2] 丁建华, 李冀龙, 高农. 车流作用下简支桥梁的随机振动分析[J]. 哈尔滨建筑大学学报, 1997, 30(2): 109-114.

[3] 周勇军, 贺拴海, 宋一凡, 等. 弹性地基上连续梁桥顺桥向地震振动分析[J]. 长安大学学报: 自然科学版, 2008, 28(2): 49-52.

[4] 桂水荣, 陈水生, 潘登. 多片梁组成的简支梁桥车桥耦合振动响应研究[J]. 中外公路, 2008, 28(4): 173-177.

[5] LI Qiang. The experimental study on coal unloading chute with skew beam and its practical calculation method [D]. Xi’an: Xi’an University of Architecture and Technology, 2004.

The longitudinal natural vibration for simply-supported beam bridge

WANG Zhen-xiang

(Hunan Changde Highway Engineering Company, Changde 415000, China)

According to thecharacteristicsof longitudinal natural vibration for simply-supported beam bridge,thenatural vibrationmodel was established: the bridge pier was simplified to cantilever beam, the laminated rubber bearing was simplified to spring at the top of bridge pier, and the superstructure was simplified to lumped mass. Then the analytical expressions of the natural vibration of simply-supported beam bridge were derived from Bernoulli-Euler beam vibration theory and D’Alembert Principle, and obtained the influence of the axial force on the natural vibration.

simply-supported beam bridge; natural vibration; frequency; Bernoulli-Euler beam

O 327

1672-6146(2012)01-0070-04

10.3969/j.issn.1672-6146.2012.01.019

2012-02-08

王振湘(1966－), 女, 工程师, 主要从事公路与桥梁施工管理工作. E-mail: 2578226097@qq.com

(责任编校:江 河)