矩阵方程行反对称解的正交投影迭代法

冯 敏,周富照,刘 将



冯 敏,周富照,刘 将

(长沙理工大学 数学与计算科学学院, 湖南 长沙, 410076)

约束矩阵方程; 正交投影迭代法; 最佳逼近解; 极小范数解

矩阵方程问题是当今计算数学中的一个热点课题. 它在结构设计、电学、固体力学、自动控制理论、振动理论、有限元、线性最优控制等领域都有着重要应用[1-4].

本文研究的问题如下:

1 求解问题Ⅰ的迭代算法及其收敛性证明

首先给出求解问题Ⅰ的正交投影迭代算法:

算法1

证明 根据算法1, 有:

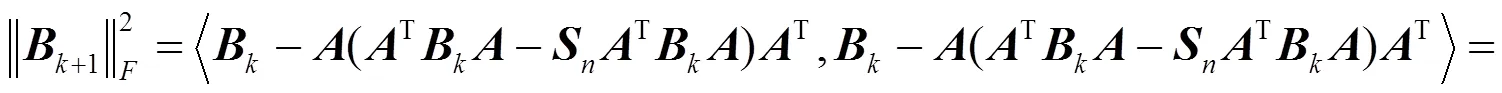
则问题Ⅰ有解的充要条件是矩阵方程组:

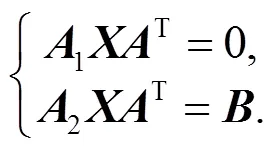
相容.

下面讨论算法1的收敛性.

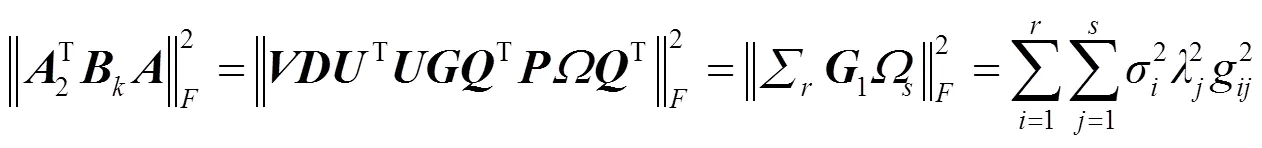
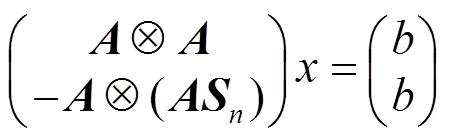
2 问题Ⅱ的解

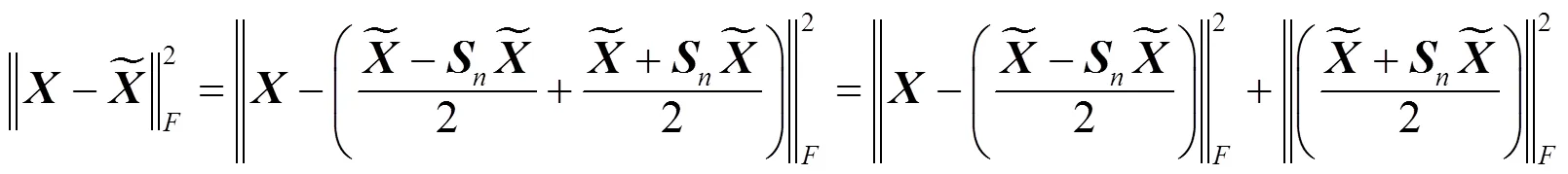
3 数值算例

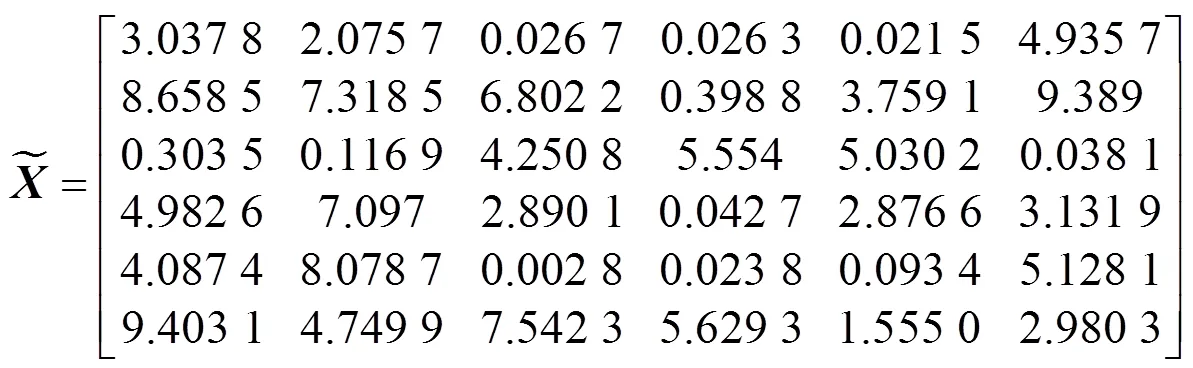
例 设

a. 求问题Ⅰ的极小范数解.

求问题Ⅱ的解.

[1] 戴华. 用振动实验最优校正刚度, 柔度和质量矩阵[J]. 振动工程学报, 1998, 1(2): 18-27.

[2] 丽君. 几类特殊线性约束矩阵方程问题及其最佳逼近问题[D]. 长沙: 湖南大学, 2008.

[3] 郭孔华, 胡锡炎. 求解约束矩阵方程的正交投影迭代法的研究[D]. 长沙: 湖南大学, 2007.

[4] 周富照. 几类约束矩阵方程及其最佳逼近[D]. 长沙: 湖南大学, 2002.

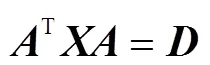
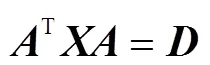
[9] 彭亚新. 求解约束矩阵方程及其最佳逼近的迭代法的研究[D]. 长沙: 湖南大学, 2005.

FENG Min, ZHOU Fu-zhao, LIU Jiang

(College of Mathematics and Computing Science, Changsha University of Science and Technology, Changsha 410076, China)

constraint matrix equation; orthogonal projection iterative method; optimal approximate solution; least-norm solution

O 241.6

1672-6146(2012)01-0019-05

10.3969/j.issn.1672-6146.2012.01.006

2011-12-05

湖南省教育厅资助项目(10C0370)

冯敏(1986-), 女, 硕士研究生, 主要从事数值代数的研究. E-mail: 569146934@qq.com

(责任编校:刘晓霞)