准一维纳米材料场发射模拟软件的研制*

邵俊文，王伟良，岳成刚，秦锡洲，夏 彧，李志兵

(中山大学物理科学与工程技术学院∥光电材料与技术国家重点实验室， 广东 广州 510275)

由于宽带隙半导体材料通常有较大的热导率和较高的饱和漂移速度，它们极有希望用来制造大功率密度及能在高温和各种恶劣环境中工作的纳微电子器件。近年来，人们合成了各种各样的宽带隙半导体纳米线，如GaN、ZnO、SiC[1-3]。实验发现它们具有优异的场致电子发射性能。我们研制了基于能态密度用有限元方法模拟准一维纳米材料场致电子发射的软件。本文介绍这个软件的理论模型、算法和使用方法。最后给出一个算例。

1 理论模型

本软件是基于李志兵等[4-5]提出的纳米材料场致电子发射双电流模型。由于纳米线内部是晶体结构[6]，我们认为仍然具有类似于块材的能带结构。而由于纳米线有很大的比表面积，把材料表面中的定域态也考虑进来。我们假设，在空间上定域态均匀地分布在表面厚度为λ的薄层中(此λ可认为是定域态的扩展宽度)。则在外界电压作用之下，导带、价带和表面态都向下移动，负电荷将在纳米线上积累。电荷密度为

ρ(r)=ρs(r)+ρc(r)

(1)

定域态中的电荷密度ρs(r)仅在上述表面薄层中不为零，在表面薄层中

(2)

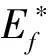
(3)

其中gc(E-Ec)为导带中的电子态密度。这些负电荷将阻止导带和价带进一步下降，而达到一个平衡。

在电流较小的时候，由准平衡近似可以认为纳米线的费米能级与衬底一致，电流较大时，费米能级将倾斜，电流与费米能级斜率的关系为

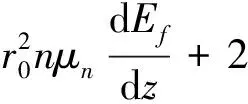
(4)

在我们的模型里，电子从基底到纳米线尖端的输运有两种电流实现。在接近基底的一端，定域态之间的跳跃电流为主；在发射端，导带上的自由电子电流为主。因此，我们的模型称为双电流模型[8]。

2 计算方法

在已知电荷密度分布ρ(r)时，空间各处的电势可由泊松方程解得，然而电荷密度ρ(r)又受该处费米能级和导带底的位置影响，而费米能级又与纳米线中的电流有关，此电流与纳米线尖端的发射电流是一致的，而发射电流又与纳米线尖端的势垒有关。所以电荷密度、电势分布、费米能级、电流这四个量互相影响，需要迭代才能解出。我们的算法如图1所示，其中Ef为费米能级，ρ为电荷密度，φ为电势，J为电流，其由两重迭代构成。首先由一个任意的费米能级和电势分布出发，由此得到电荷分布，再由电荷分布求出一个新的电势分布，再求电荷分布，如此迭代直到电荷和电势同时收敛。然后再根据电势分布在纳米线尖端用WKB近似文献[9]求出发射电流，再由式(4)求出费米能级分布。由新的费米能级分布再求出新的电荷分布……如此构成第二重迭代，迭代收敛时便得到了电荷密度、电势分布、费米能级和电流。

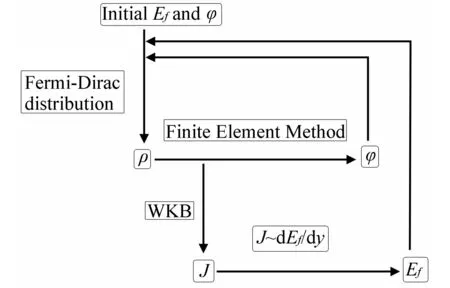
图1 算法流程

3 使用方法

3.1 设定材料属性

设定材料属性有两种方法。

1)手动输入。

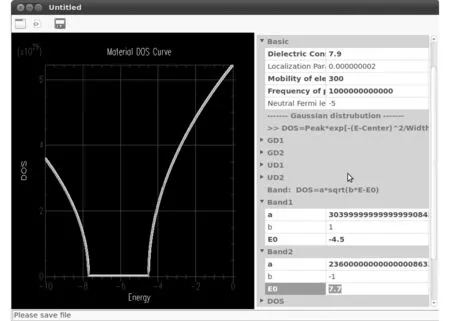
图2 输入ZnO材料属性的例子

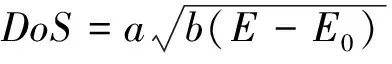
2)从VASP的计算结果中导入。

如图3，用户须指出材料的介电常数、迁移率、中性费米能级。态密度则可从VASP计算出的DOSCAR中导入。本软件会将这些数据保存成材料数据文件供以后使用。

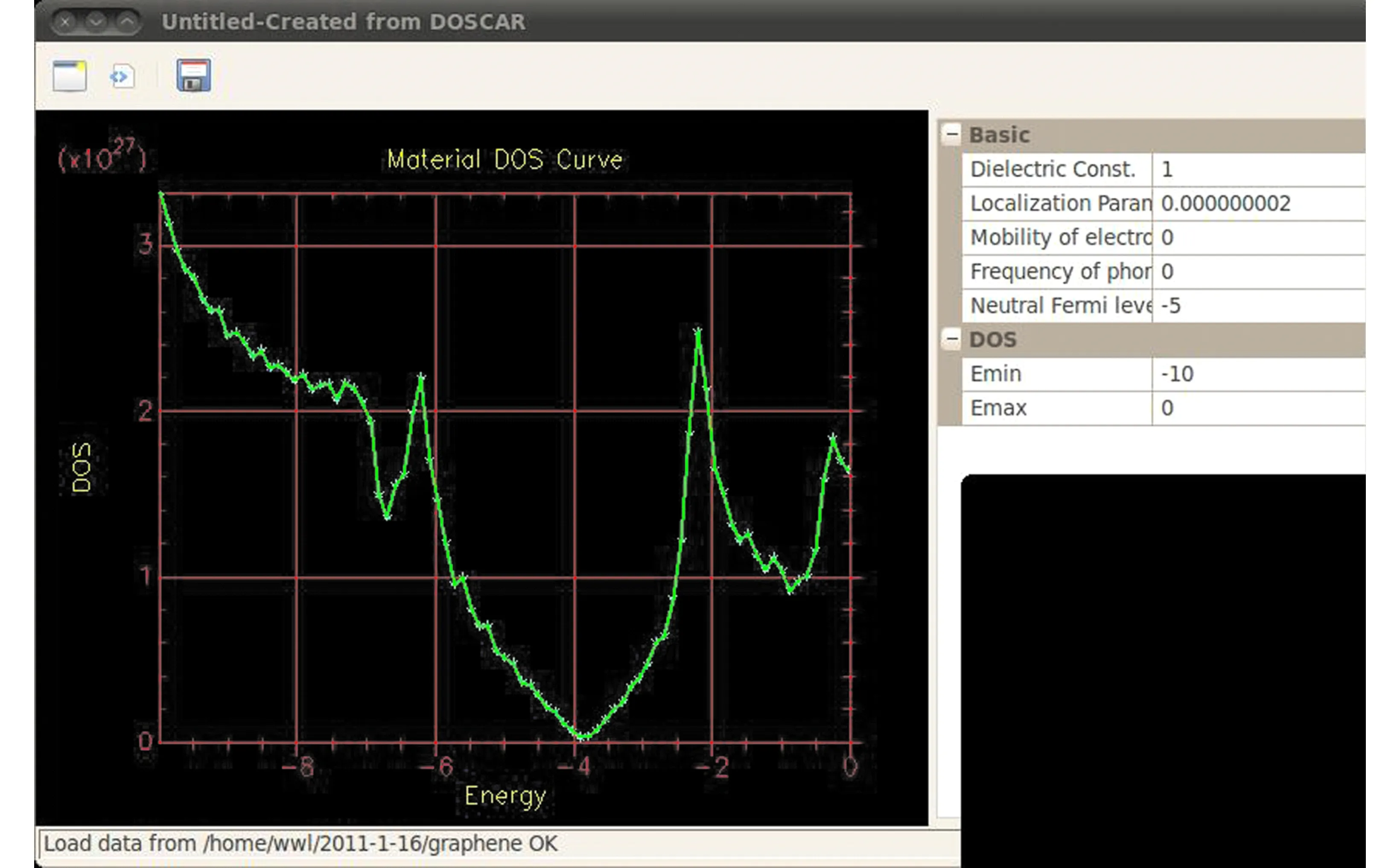
图3 导入graphene材料属性的例子

3.2 描绘器件结构

用户可用图形界面描绘器件结构(用多边形和椭圆组合出各种形状，二维图形实际对应的是轴对称的三维结构，对称轴为y轴)，同时指定每一个区域属于哪种材料。

具体步骤：

1)从主界面(图4)右边Material中选择材料文件。

2)在工具栏中点选多边形或椭圆，在主窗口中绘图(每一个图形都可以通过双击打开属性对话框来微调其坐标)。

3)在右边Grid Count框中填入欲划分的格点数(数字越大计算越精确，计算速度越慢)。

3.3 设定边条件

边条件可以在不同区域不同，各个区域的边条件若无法统一用一个表达式，可以分开多次来设置。步骤如下：

1)在图5窗口上方的range是指定本次设置的边条件对这个范围之内的边界生效；

2)选择Neumann或Dirichlet型边条件；

3)或选择Dirichlet型边条件，则需指出边界值，边界值可以是边界坐标x,y的函数。

4)设置完点OK，可以再打开边条件设置窗口设置另一个区域的边条件。

3.4 计算电势、电荷密度分布、费米能级、发射电流

计算完成后，输出结果potential.out和Ef.dat。其中potential.out第一列为格点的横坐标，第二列为纵坐标，第三列为电势，第四列为电荷密度，第五列为势能(即导带底减电势)。Ef.dat的第一列为格点的横坐标，第二列为纵坐标，第三列为费米能级。图6、7是与图4的结构相对应的电势分布、电荷密度分布(仅在纳米线的末端表面电荷密度才不为零，纳米线靠近衬底处有电荷分布是因为肖特基结)。与图4相对应图中下方是阴极(电势定为0 V)，上方是阳极(电势定为25 V)，中间栅极的电压定为20 V。图中用阴影表示纳米线、SiO2和金属栅极的位置。

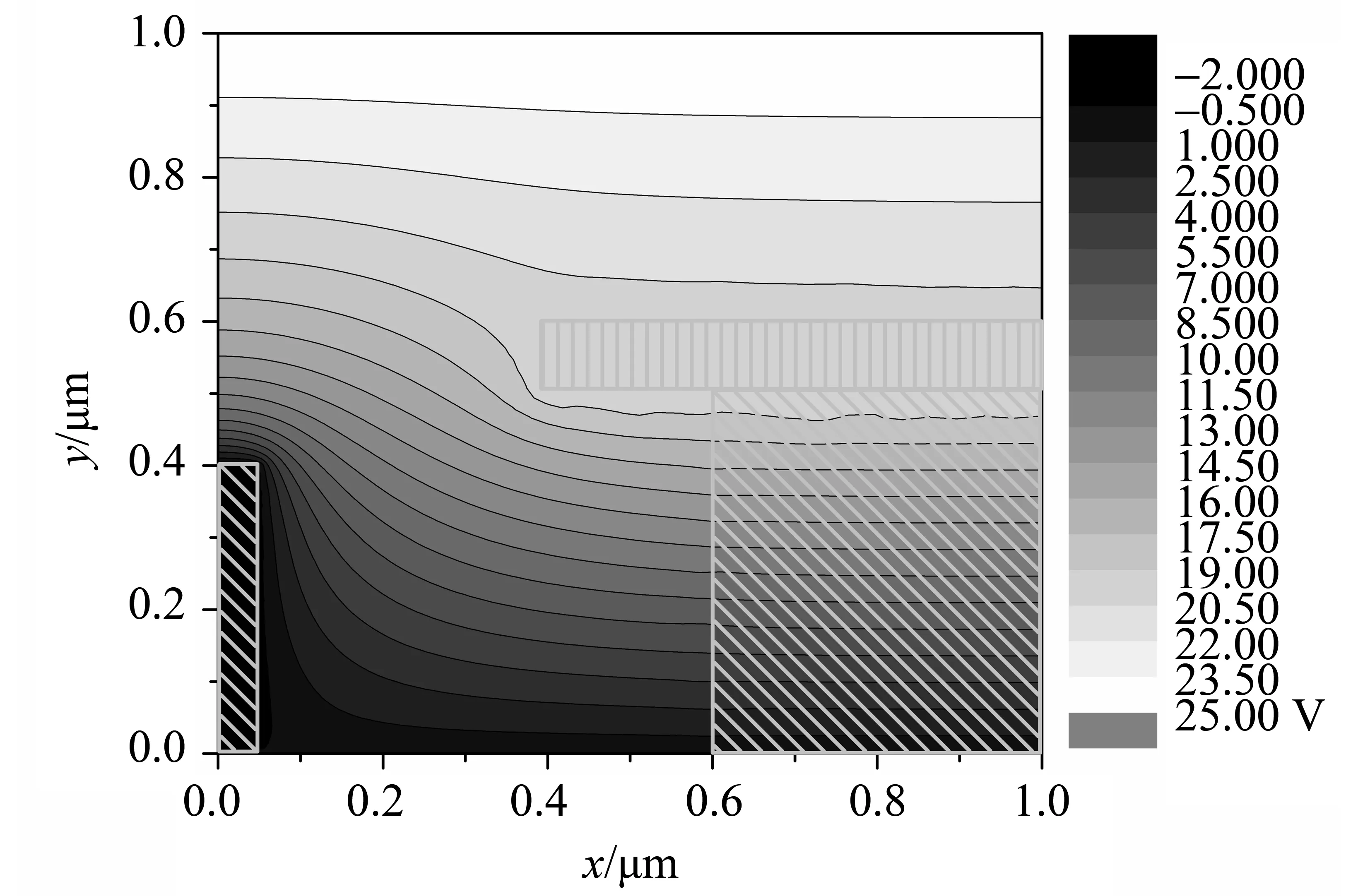
图6 用Origin作出的电势分布图

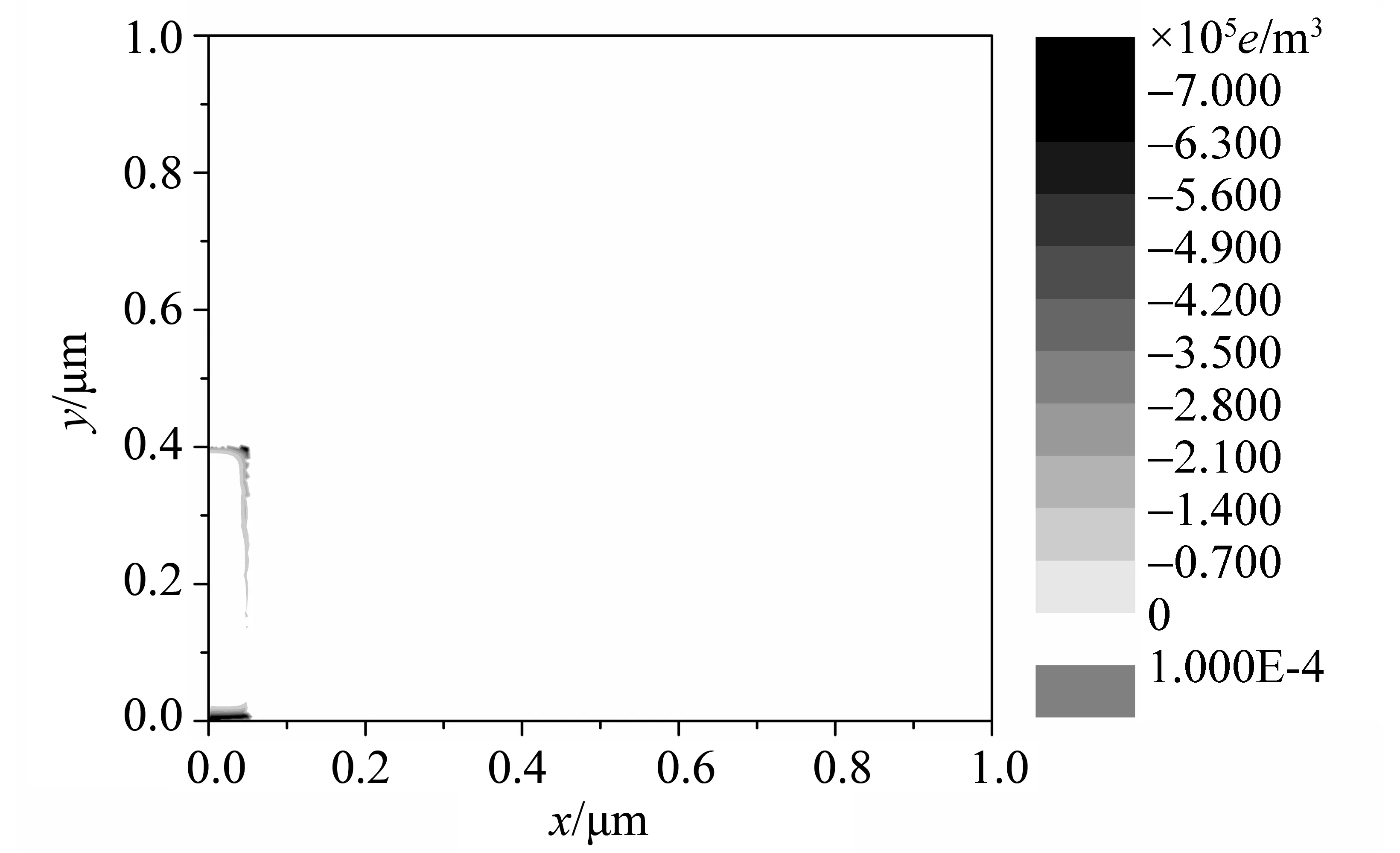
图7 用Origin作出的与图4、6相对应的电荷分布图

4 算 例

下面我们计算文献[11]中Fig.5 (c)所示的单根硼纳米线的场致电子发射电流。其中硼的功函数为4.3 eV，文献[12]带隙为1.6 eV。文献[13]图8中纳米线的半径为25 nm，与阳极探针的距离为0.5 μm，纳米线表面层的厚度为2 nm，在表面层使用的是在禁带中加了态密度为常数1025m-3eV-3的硼，阳极探针的半径为0.25 μm。图8与文献[11]中Fig.5 (c)的上下是反过来的，即纳米线在下，阳极在上。靠近y轴蓝色区域为半径25 nm的硼纳米线，靠近y轴黄色区域为半径0.25 μm的阳极探针，两者间距为0.5 μm。图9是计算得到的发射电流与相应的FN曲线，与文献[11]中Fig.5(d),(e)一致。

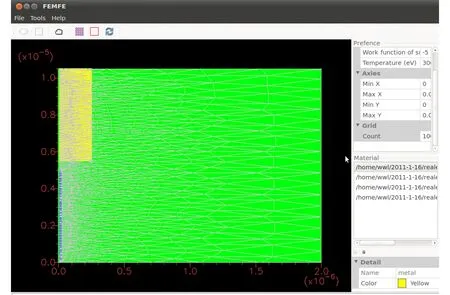
图8 与文献[AIP conf.proc.1173 (2009)317]中Fig.5 (c)对应的硼纳米线场致电子发射装置

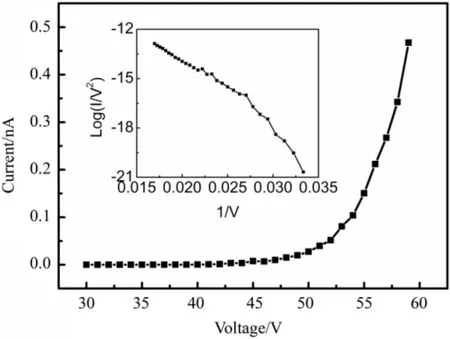
图9 与图8对应的电流-电压曲线，插图是相应的FN曲线

5 结 论

本文介绍了准一维纳米材料场致电子发射模拟软件的研制。本软件是基于一个纳米材料场致电子发射的双电流模型，自洽地计算电势、电荷密度、费米能级的分布和发射电流。本软件是图形界面，可以计算任意的轴对称的器件结构。本文给出了一个算例，按照文献[11]的实验装置，计算了单根硼纳米线的场致电子发射，得到的结果与实验一致。

参考文献：

[1]HAN W,FAN S,LI Q,et al.Synthesis of gallium nitride nanorods through a carbon nanotube-confined reaction[J].Science,1997,277(5330):1287-1289.

[2]LEE C J,LEE T J,LYU S C,et al.Field emission from well-aligned zinc oxide nanowires grown at low temperature[J].Applied Physics Letters,2002,81(19):3648-3650.

[3]WONG K W,ZHOU X T,AU F C K,et al.Field-emission characteristics of SiC nanowires prepared by chemical-vapor deposition[J].Applied Physics Letters,1999,75(19):2918-2920.

[4]LI Z B,WANG W L,DENG S Z,et al.Field-induced insulator to semimetal transition and field electron emission of nanorods of semiconductors of wide energy band gaps[J].arXiv:cond-mat/0511418,2005.

[5]LI Z B,WANG W L,XU N S.Field electron emission of nanorods of semiconductiors of wide energy band gaps[C]∥Technical Digest of the 18th International Vacuum Nanoelectronics Conference，Oxford: IEEE,2004.

[6]DENG S Z,WU Z S,ZHOU J,et al.Synthesis of silicon carbide nanowires in a catalyst-assisted process[J].Chemical Physics Letters,2002,356(5/6):511-514.

[7]MOTT N F.Conduction in non-crystalline materials 3:Localized states in pseudogap and near extremities of conduction and valence bands[J].Philosophical Magazine,1969,19(160):835.

[8]LI Z B,WANG W L,DENG S Z,et al.Field electron emission from nano wires of wide energy band gaps[C]∥International Vacuum Nanotechnique Conference,UK:Oxford University,2005.

[9]FROMAN N，FROMAN P O.JWKB approximation: Contributions to the theory[M].Amsterdam: North-Holland,1965.

[10]刘恩科,朱秉升,罗晋生.半导体物理学[M].4版.北京: 国防工业出版社,1994:52.

[11]TIAN J F,CAI J M,HUI C,et al.Boron nanowires for flexible electronics and field emission[J].AIP Conference Proceedings,2009,1173:317.

[12]LIU F,TIAN J F,BAO L H,et al.Fabrication of vertically aligned single-crystalline boron nanowire arrays and investigation of their field-emission behavior[J].Advanced Materials,2008,20:2609.

[13]HELLWEGE K H.Landolt-bornstein numerical data and functional relationships in science and technology[M].Berlin: Springer,1983.