基于可分解的多目标进化算法的PDN阻抗的优化

赵志超，张 申，张 辉

(1.西安电子科技大学电子工程学院，陕西西安 710071;2.西安电子科技大学天线与微波技术国家重点实验室，陕西西安 710071)

在高频时，由于过孔或晶体管切换时电源引脚吸收瞬时电流，而稳压源VRM由于电源地平面噪声的影响，无法及时提供恒定电压，这时就会从电源地平面吸取大量电荷造成压降，如果压降超过5%波纹技术规范就会导致电源无法正常工作，造成严重的电源完整性问题。因此，如何解决电源噪声问题为平面提供低阻抗路径，成为电源分配网络设计的关键。将电源允许的最大电压波动容限转化为频域的一个参数:目标阻抗。现在把问题转化为如何优化电源分配网络(PND)，以提供低阻抗，使得它在截止频率内小于目标阻抗。为优化PDN，最重要的两个优化目标是去耦电容器的个数和种类的选择。设计者可以通过迭代改变这些参数来控制PND谐振以减小阻抗峰值[1]。目前，对于系统级的PND的设计是基于一些单目标随机的算法，例如遗传算法[2]和模拟退火[3-4]，而应用单目标方法优化多目标问题会造成较大的偏差，无法更加准确地逼近PF。自2003年以来，进化多目标算法前沿的研究呈现出新的特点，对于多目标优化问题本身性质的研究也在深入。文中所应用的基于分解的多目标进化算法(MOEA/D)是近两年来在进化计算研究领域内的先进成果。它将多目标优化问题转换为单目标优化问题，该算法将逼近整个Pareto前沿面(PF)的问题分解为一定数量的单目标优化问题，然后用进化算法同时求解这些单目标优化问题。算法维持一个由每个子问题当前最优解组成的种群，子问题之间的近邻关系定义为子问题权重向量之间的距离，每个子问题的优化过程通过与其近邻子问题之间的进化操作完成[5]。

1 PDN中的去耦电容

1.1 电源分配网络的设计

本文采用电源分配网络(PDN)的集总等效模型。首先是稳压器模块(VRM)，如图1所示，模型可以简化为一个串联的电阻和电感。从DC到大约50 kHz的频率范围内，VRM的阻抗非常低，可以满足芯片对瞬态电流的要求。

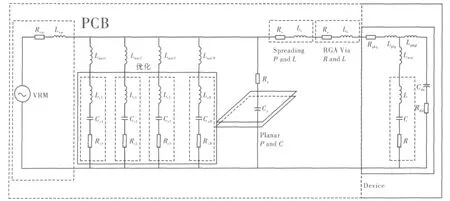
图1 PDN拓扑的集总等效模型

设计PDN的第一步是确定目标阻抗，必须分别对电路板上所有芯片的各个电压轨道进行独立设计。对于每个电压轨道，目标阻抗可能会随频率而改变，这取决于芯片各自的电流频谱。当一频率分量的电流流过给定阻抗曲线的PDN时，在PDN上会产生电压噪声并且电压降低，把电压的5%规定为PDN中可接受波纹最大压降，它所对应频域内最大的阻抗，即目标阻抗。可以得到

由于规定波纹指数是5%，所以式(1)可表示为

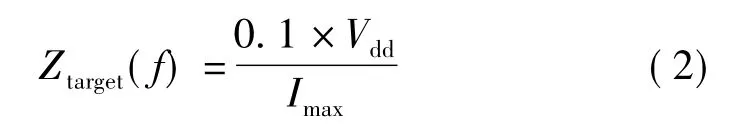
其中，Vdd为轨道电压;Imax为芯片的最大电流。只有当阻抗曲线低于目标阻抗时，PDN符合设计要求，如果PDN阻抗某些峰值超过目标阻抗，这时需要添加去耦电容来抑制这些峰值，使其低于目标阻抗。

1.2 去耦电容网络的设计

去耦电容器网络的设计是PDN设计的重点，它决定了PDN的性能。一般PDN中都会包含各式各样的电容器，对于如何分配去耦电容器及其位置并没有达成共识。当高频时VRM不能提供低阻抗，此时，设计PDN阻抗曲线的策略就是选择合适的容值种类和个数的电容器以保持峰值阻抗低于目标阻抗。

要降低峰值阻抗就是要减小较大电容的串联等效电感(ESL)或并联更多电容器。这些电容的容值种类可以相同也可以不同。高频时电容器的阻抗完全取决于ESL的并联值，假设它们的ESL值都相同，该条件变为

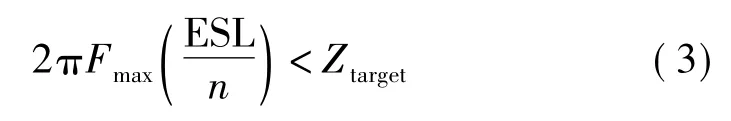
其中，ESL为单个电容器的等效串联电感;n为满足目标阻抗所需并联电容器的个数;Fmax为板级PDN设计起作用的最高频率，即截止频率。

式(3)从理论上确定了为满足目标阻抗所需并联电容器的最少个数[6]

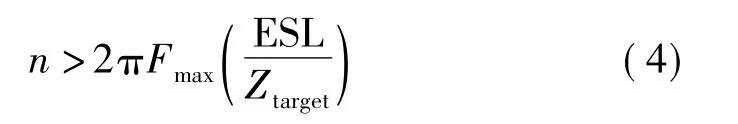
在不考虑容值的情况下，为减小所需电容器的个数，必须减小单个电容器的ESL。

PDN的输入阻抗主要由去耦电容的个数和种类所决定

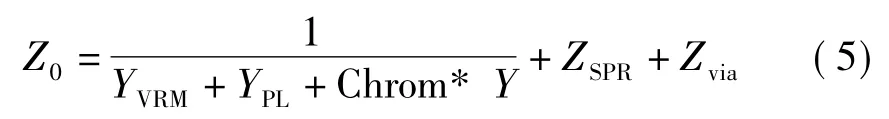
其中，YVRM是稳压源VRM的电导;YPL是平面电容的电导;Chrom*Y为所添加的总电容值;ZSPR是分布电感的阻抗;Zvia是过孔电感阻抗。

2 多目标问题及算法

多目标优化问题(MOP)在现实中应用广泛，一般需要同时优化两个或两个以上的目标并且这几个目标之间相互冲突，一个解对于某个目标可能是可能较好，而对于其他目标可能较差，因此存在一个折衷解的集合，称为Pareto最优解或非支配解集。对于多目标问题最初的方法就是通过加权等方法把它们转化为单目标的问题，然后用数学规划法来求解，但每次只能得到一种权值情况下的最优解，它仅仅是多目标问题的Pareto前沿(PF)的一个解，而传统的数学规划方法往往效率很低，且它们对权重值或目标给定的次序较敏感。针对传统数学方法的局限性，越来越多的研究者试着通过直接的方法去逼近PF。提出了很多先进的多目标算法，一些通过使用数学模型或基于进化算法来逼近PF。其中，一种算法成功地将数学规划中常用的分解方法引入到进化多目标领域，而且可以直接采用进化算法求解单目标优化问题，文中即采用此算法:基于分解的多目标进化算法(MOEA/D)。

在本文中，使用MOEA/D同时优化去耦电容的种类和个数。文献[7]分别描述了MOPs和MOEA/D的构架。

2.1 MOPs的描述

目前，许多问题都是多目标优化的问题，单目标问题只是特例。多目标问题可以描述如下

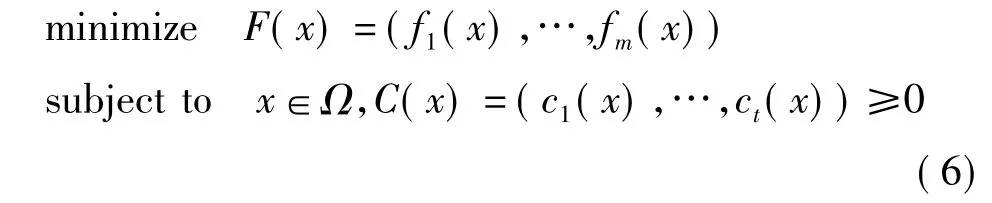
其中，Ω是决策变量空间;C(x)代表问题约束和定义决策空间的可行域。F∶Ω→Rm由m个实值函数组成;Rm为目标函数空间。

为平衡各个目标，定义各个解之间的支配关系。现在令 u=(u1，…，um)，v=(v1，…，vm)∈Rm是两个向量，对于所有 f(x)的 i=1，…，m，如果有 ui≤vi并且u≠v，则称u能支配v。如果不存在点x*∈Ω使得支配f(x*)，则称点x*∉Ω是最佳Pareto。所有Pareto最佳点叫作Pareto集合(PS)，与PS对应的所有目标向量叫作Pareto前沿(PF)，其中 PF={F(x)∈Rm/x∈PS}[8]。

2.2 基于分解的MOEA

MOEA/D使用分解方法把一个MOP分解成一系列的单目标优化问题。MOEA/D尝试去集体和同时优化这些单目标以代替其他进化算法的直接逼近Pareto前沿面(PF)，因为这些SOPs的每一个最优解是给定MOP的一个Pareto最优解。这些最优解的集合就是一个pareto前沿面的逼近。每个子问题在当前解集中都能找到一个局部最优解。用权重响亮的欧氏距离来描述子目标中邻居之间的远近程度，而这个权重向量就是m个子目标的聚合系数，通常认为相邻的子问题的最优解应该非常接近。子问题可以描述为

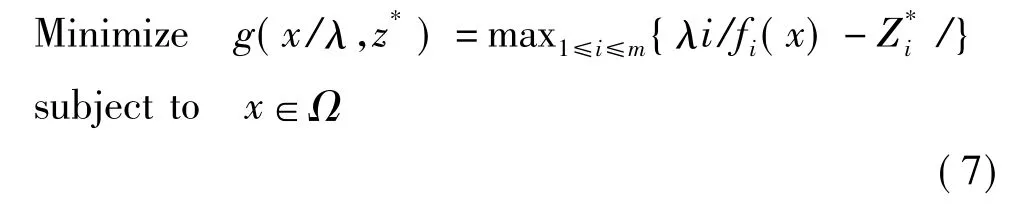
其中，λ =(λ1，…，λm)是一个权向量的集，对于所有的。

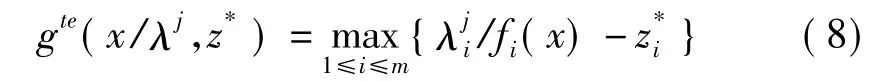
MOEA/D叙述如下:

(1)输入。1)决定变量。2)N为MOEA/D中考虑的子问题的数目。3)λ1，…，λN为均匀分布的N个权重矢量。4)T为在每个权重矢量邻居中的权重矢量的数量。5)停止判据。

(2)输出。1)PS的近似值为 x1，…，xN。2)PF的近似值为F(x1)，…，F(xN)。

3 实验数据及结果分析

3.1 实验数据

将去耦电容器的截止频率 Fmax、等效串联电感ESL和最大电流Imax作为决定变量，通过改变这些参数来改变电容器的个数。同时将电容器的种类和个数作为需要优化的目标函数。将分解后的每个子问题中的目标阻抗Ztargetj作为每个子问题的参考点Z*，通过调节决定变量来改变输入阻抗Z0，使得它在截止频率内不要超过目标阻抗。在本文中取几种组合作仿真验证，MOEA/D算法中把参数设为:进化代数60代;种群大小为150;邻居个数为30个;分解方法为Tchebycheff算法。在 PND 中，ZVRM=0.001 Ω;ZPL=0.003 Ω;RSPR=0.002 Ω;Rvia=0。

选取3组实验数据并得到实验结果。第一组选取的目标阻抗Ztarget为0.1 Ω，截止频率F max为50 MHz，获得的电容器的方案如表1所示，PDN阻抗曲线如图2所示。第二组选取的目标阻抗Ztarget为0.2 Ω，截止频率Fmax为100 MHz，获得的电容器的方案如表2所示，PDN阻抗曲线如图3所示。第三组选取的目标阻抗 Ztarget为 0.2 Ω，截止频率 Fmax为 80 MHz，获得的电容器的方案如表3所示，PDN阻抗曲线如图4所示。表1～表3中电容器种类限制均为6种。

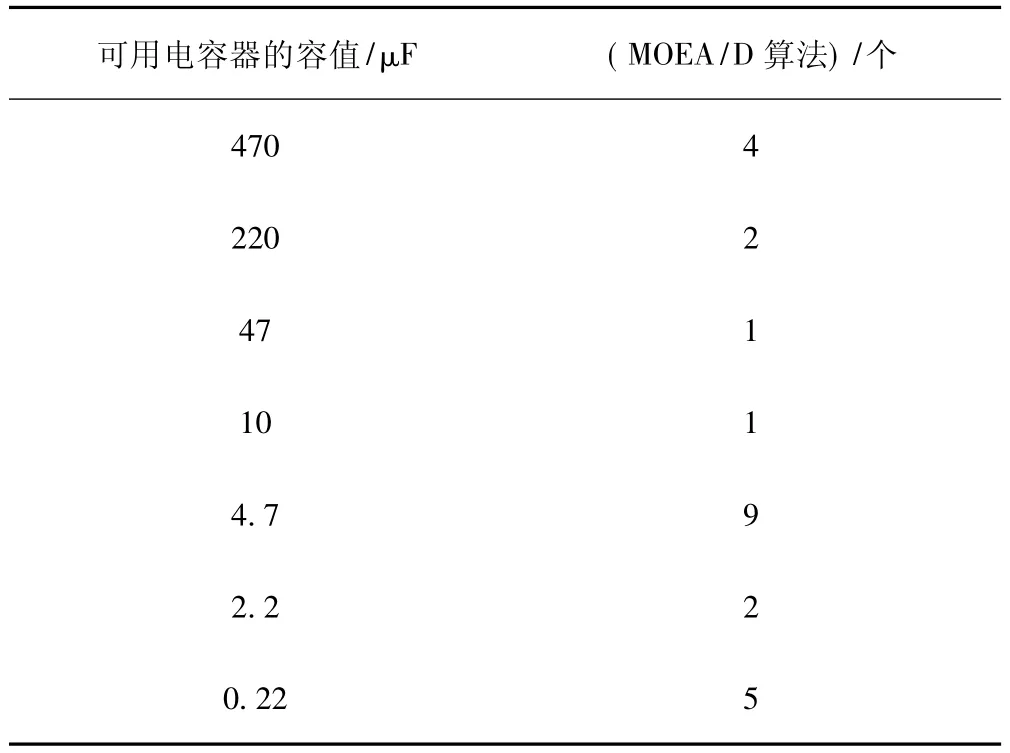
表1 3种设计方法的电容器方案(目标阻抗0.1 Ω，截止频率50 MHz)

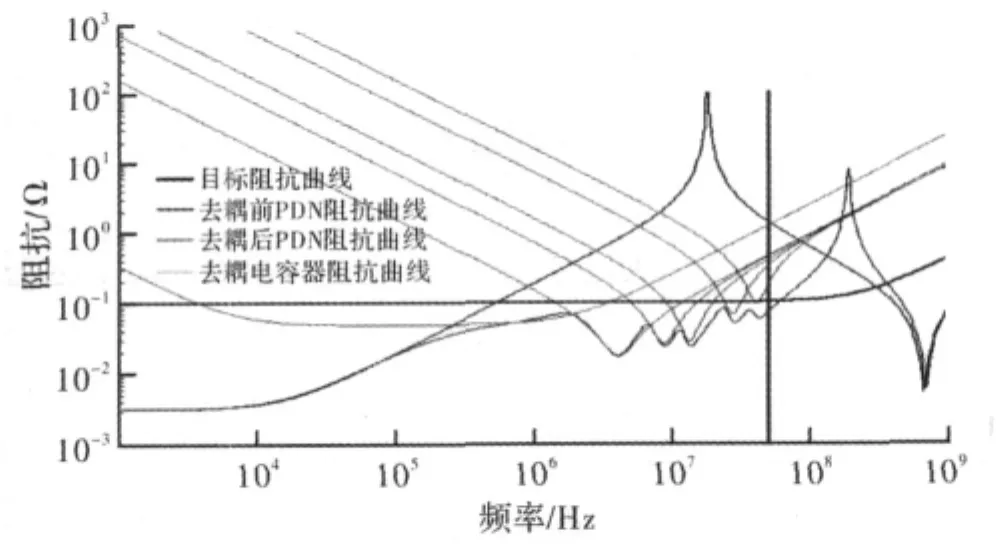
图2 MOEA/D算法的PDN阻抗曲线(目标阻抗0.1 Ω，截止频率50 MHz)

表2 3种设计方法的电容器方案(目标阻抗0.2 Ω，截止频率100 MHz)

图3 MOEA/D算法的PDN阻抗曲线(目标阻抗0.2 Ω，截止频率100 MHz)

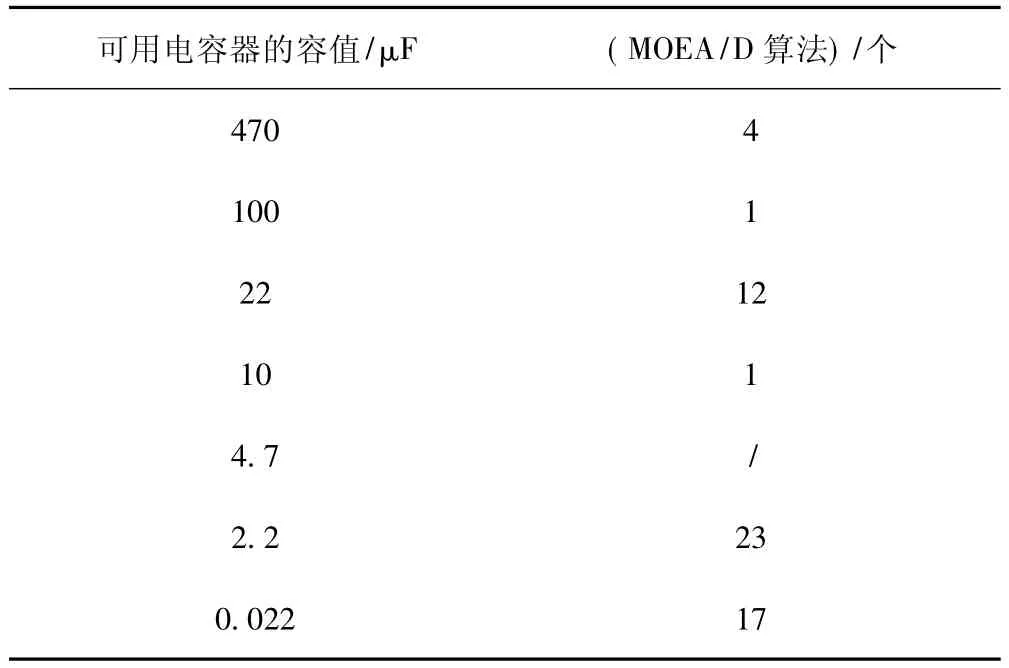
表3 3种设计方法的电容器方案(目标阻抗0.2 Ω，截止频率80 MHz)

图4 文中方法的PDN阻抗曲线(目标阻抗0.2 Ω，截止频率80 MHz)

3.2 实验结果分析

实验数据显示，当频率为50 MHz时，需要的去耦电容器是24个;频率为80 MHz时，去耦电容器的个数是58;当频率为100 MHz时，去耦电容器的个数是104。这表明随着频率的升高，所需的去耦电容器也越多。高频时PND阻抗明显增大，芯片噪声严重，从图中我们可以看到，未加去耦电容的PDN曲线在高频时超过了目标阻抗，并形成尖峰。而添加相应的去耦电容后将PND曲线尖峰压到目标阻抗之内，有效地抑制了噪声。可以看到，在截止频率内PDN阻抗小于目标阻抗，满足在截止频率内阻抗设计的要求。

4 结束语

文中使用了基于分解的多目标进化算法(MOEA/D)来优化电源分配网络(PDN)，去耦电容网络中的两个目标函数电容器的种类和个数被MOEA/D分解成两个单目标，并同时被优化。它们的解是一个折衷的优化解而并非是各自的最优解，实验证明，它们逼近Pareto Front(PF)。实验结果给出了优化后电容器的种类和个数，数据显示，截止频率越高所需的电容个数越多，才能使PDN阻抗限制在规定的截止频率内满足设计需要。

[1]ENGIN A E.Efficient sensitivity calculations for optimization of power delivery network impedance[J].IEEE Trans Electromagn Compat，2010，52(2):1511-1519.

[2]BHARATH K，ENGIN E，SWAMINATHAN M.Automatic package and board decoupling capacitor placement using genetic algorithms and mfdm[C].In Proc.45th ACM/IEEE Des.Autom Conf(DAC 2008)，2008:560-565.

[3]CHEN J，HE L.Efficient in-package decoupling capacitor optimization for i/o power integrity[J].IEEE Trans Compat-Aided Design Integr Circuits Syst，2007，26(4):734-738.

[4]ZHENG H，KRAUTER B，PILEGGI L.On-package decoupling optimization with package macromodels[C].In Proc.IEEE Custom Integr Circuits Conf，2003(9):723-726.

[5]GONG M G，JIAO L C，YANG D D，et al.Evolutionary mutilti-objective optimization algorithms[J].Journal of Software，2009，20(2):271-289.

[6]ERIC B.信号完整性分析[M].2版.李玉山，李丽平，译.北京:电子工业出版社，2005.

[7]ZHANG Qingfu，LI Hui.MOEA/D:A Multiobjective Evolutionary Algoritm Based on Decomposition [J].IEEE Trans Evol Comput，2007，11(6):458-463.

[8]MIETTINEN K.Nonlinear multiobjective optimization[M].USA:Kluwer Academic，1999.