技术进步对我国经济增长影响的实证分析

2012-04-29张佑泽

会计之友 2012年15期

张佑泽

【摘要】在国民经济发展新时期，如何运用科学技术来实现我国经济又好又快地发展，显得尤为关键。文章根据索洛模型理论，将科技活动人员数和科技活动经费支出因素从劳动力投入和资本投入中剥离出来，进一步具体化柯布——道格拉斯生产函数的形式，从而更有针对性地测算技术投入对经济增长的贡献率。研究结论表明：科技活动人员数以及科技活动经费支出对经济增长均具有显著影响，而且，科技活动经费支出对经济增长的贡献率要大于科技活动人员的贡献率。

【关键词】技术进步；经济增长；柯布——道格拉斯生产函数；计量分析

一、技术进步对经济增长影响的理论分析

所谓技术进步，通常应包括技术发明、技术开发、技术推广和技术应用，有狭义和广义两种理解。科技进步贡献率中的“科技进步”指的是广义的技术进步。广义技术进步，是指一种存在于一切社会经济活动中有目的的发展过程，它不仅包括了狭义技术进步所指的生产技术水平的变化，而且还包括了管理技术、服务技术以及智力投资的变化。其中需重点强调一下人力资本，人力资本是指劳动者的知识程度、技术水平、工作能力以及健康状况方面价值的总和，它也是技术进步的一个重要方面。经济增长是指一个国家或地区在一定时期，社会财富、生产增长、总产出的总量和人均量的完全增长，衡量经济增长的指标常用的是GDP或GNP的增长率。

技术进步与经济增长之间是相互影响和作用的：一方面，技术进步是经济增长的内在动力，经济增长可以通过两条途径实现：外延扩大再生产和内涵式的扩大再生产，而技术进步的实质是要提高实体性生产要素的生产效率。表现在：第一，技术进步已成为现代经济发展的主要驱动力；第二，科技进步促进经济结构的优化调整；第三，依靠技术进步实现经济增长方式的根本性转变。另一方面，经济增长是技术进步的经济基础，具体来说：首先，经济发展是技术发展的物质基础；其次，经济发展决定着技术发展的方向；再次，经济发展改善着技术进步的条件与环境。

技术进步与经济增长之间的相互影响和作用是纷繁复杂的，同时技术进步包括的因素是多样的，有些因素甚至是抽象的、难以量化的；而经济增长也有不同的计算口径。本文在对国内外研究现状及研究方法分析的基础上，对柯布—道格拉斯生产函数进行改进，重点分析技术进步中的科技活动人员和科技活动经费支出这两个重要因素对经济增长的贡献率，并根据建立的计量经济模型，提出相应的对策建议。

二、国内外研究现状

国际上，技术进步的测定模型产生于20世纪20年代。关于技术进步及其测定的文献非常之多，以至于20世纪70年代中期以来，无人能够对技术进步的研究写出一份比较完整的综述。在迄今为止的20多位诺贝尔经济学奖得主中，至少有一半以上的人对技术进步或其测定作过较深入的研究。但直到目前，全世界经济学界对技术进步测算的理论与方法，仍存在许多争议，还难以形成一套公认的测度模型。这主要是由于技术进步具有难以量化的特征，要想精确地度量技术进步与经济增长的关系十分困难。归纳起来，科技进步的测定模型主要有：“柯布——道格拉斯”生产函数、丁伯根模型、索洛模型、丹尼森模型。其中应用最广泛的是以“柯布——道格拉斯”生产函数为基础的索洛模型。其基本思路是：经济增长中扣除劳动力、资本投入数量增长因素之后，所有产生作用的其它因素的总和，都是由技术进步带来的。常用形式为：Y=ALαKβ（其中，Y、A、L、K分别代表产量、技术水平、投入的劳动量和资本量，α、β分别表示劳动和资本的产出弹性）。索洛提出的模型，定量地揭示了广义技术进步对经济增长的作用，在世界经济学界产生重大影响。

我国对科技进步贡献率研究始于20世纪80年代，目前国内对经济增长理论的研究处于对国外经济增长模型的消化、吸收阶段。我国学者研究使用的方法主要是以“柯布——道格拉斯”生产函数为基础的索洛模型，通常是在此基础上进行改进。例如，董西明（2006）运用增长速度方程y=?坠+αk+β1测度了山东省劳动、资本、科技进步对经济增长的贡献率，认为资金对山东经济增长的贡献是“举足轻重”的。田茂峰（2007）应用“柯布——道格拉斯”生产函数Y=ALαKβ，说明了我国经济增长的主要动力来自投资。赵小芳等（2008）采用皮尔逊（Pearson）相关系数，测度了科技进步与区域经济发展的相关性，主要说明了我国科技进步与区域经济发展的大部分指标具有显著的正相关关系。同时，也有一些学者对“柯布——道格拉斯”生产函数的数据拟合方式进行改进使之更具有针对性和中国特色。例如，齐微通过建立多项式拟合模型和线性规划模型来处理生产数据，并通过误差分析来验证该多项式拟合模型是完全符合数据的。但通过使用线性回归方法求得的柯布——道格拉斯生产函数，通过对其进行误差分析可以知道柯布——道格拉斯生产函数与原始数据的误差比多项式拟合模型下的误差小得多。

三、技术进步对经济增长影响的实证分析

（一）模型构建及优化

1.变量选择及模型构建

为了重点分析大中型企业中科技活动人员以及科技活动经费支出对经济增长的影响，通过对柯布——道格拉斯生产函数进行如下改进来进行拟合：

Y=AL1αL2βK1?酌K2?浊（1）

其中，Y——工业总产值；A——除了劳动投入、资本投入、科技活动人员以及科技活动经费支出之外的技术因素之和；L1——年末从业人员与科技活动人员数之差；L2——科技活动人员数；K1——科技活动经费支出之外的资金投入，数值上等于固定资产投资和流动资产年末余额减去科技活动经费支出；K2——科技活动经费支出额；α、β、?酌、?浊分别为L1、L2、K1、K2的产出弹性。

考虑建立工业总产值与各因素之间的多元线性回归模型，因此需要对式（1）两边取自然对数，根据取过对数的数据建立的模型其意义是不变的，由此可以得到式（2）：

InY=InA+αInL1+βInL2+?酌InK1+?浊InK2（2）

为表示方便，再令：Z=InY，X1=InL1，X2=InL2，X3=InK1，X4=InK2，m=InA

则式（2）转化为式（3）：

Z=m+αX1+βX2+?酌X3+?浊X4（3）

式（3）将是我们建模后得到的模型形式，是我们可以分析的形式。

2.数据搜集与转化

本文原始数据来源于中国统计年鉴（2010）中的2000年至2009年十年间的大中型企业相关指标，其中Y、L2、K2的值可以直接获得，L1的值等于年末从业人员与科技活动人员数之差，K1数值上等于固定资产投资和流动资产年末余额减去科技活动经费支出，而年末从业人员数、固定资产投资和流动资产年末余额也可直接获得（见表1）。

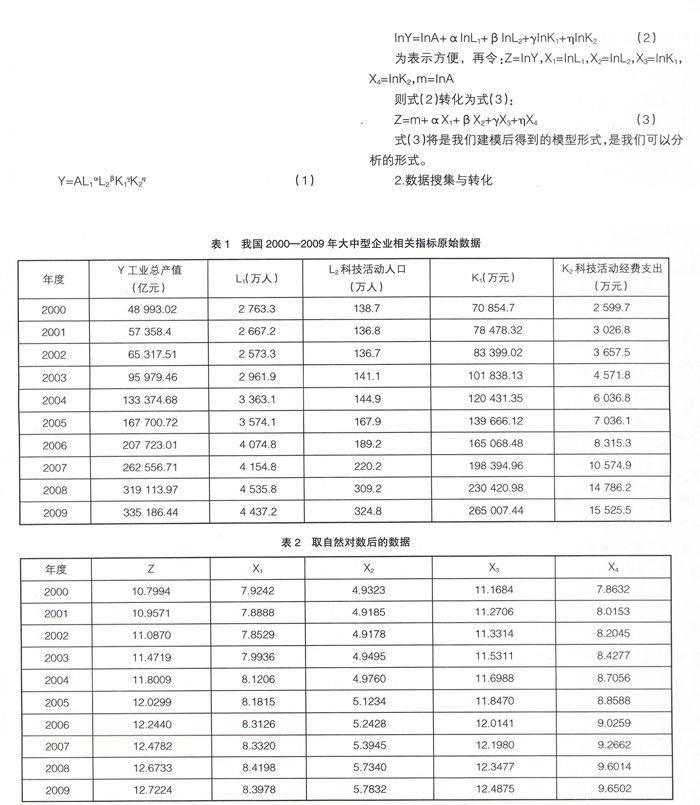
根据本文的建模要求，对原始数据取自然对数后得到表2数据。

3.数据分析

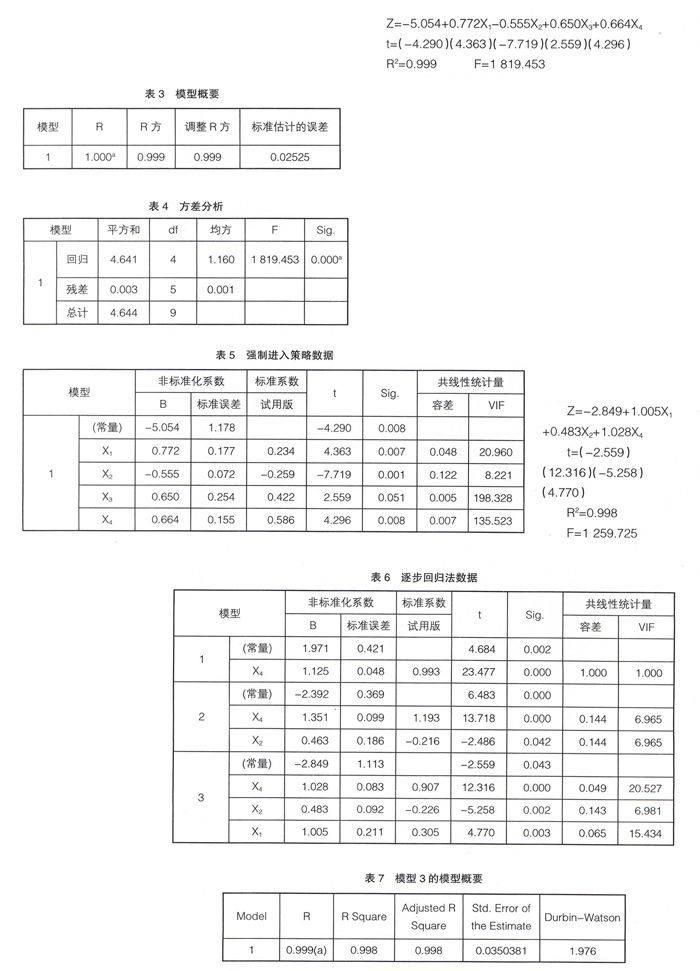
通过统计软件SPSS17.0，采用Enter强制进入策略对自变量进行分析，最初的运行结果见表3、表4、表5。

从表3可见，调整的判定系数R2=0.999，方程的拟合优度很高，因变量被解释的部分较多，未被解释的部分较少。这说明影响因变量Z的主要因素均已纳入模型，没有丢失关键影响因素。

从表4中可见F统计量的观测值为1 819.453，对应的概率p值接近0，明显小于显著性水平α（0.05），所以可以认为自变量与因变量的线性关系比较显著，建线性模型是正确的。

从表5中可得初步回归模型为：

Z=-5.054+0.772X1-0.555X2+0.650X3+0.664X4

t=（-4.290）（4.363）（-7.719）（2.559）（4.296）

R2=0.999 F=1 819.453

由此可见，该模型调整后的可决系数为0.999，非常高，F检验值为1 819.453，整个模型明显显著。但是当显著性水平为0.05时，X3系数的t检验不太显著。同时，常数项系数与X2系数的符号与预期的相反，这表明很可能存在多重共线性。从容忍度和膨胀因子来看，容忍度普遍较小接近0，膨胀因子除X2外普遍大于10，说明方程存在比较严重的多重共线性，需要对方程进行进一步的优化。

4.模型优化

对变量进行Stepwise(逐步回归法)筛选以消除多重共线性，可得表6、表7。

应用逐步回归法得到以上三个模型，说明三个模型皆消除了多重共线性，虽然模型3共线性相对来说严重一些，但考虑到其包括了更多的变量，更符合经济意义一些，因此，我们得到的优化模型是第3个模型（方差分析表省略）：

Z=-2.849+1.005X1

+0.483X2+1.028X4

t=（-2.559）

（12.316）（-5.258）

（4.770）

R2=0.998

F=1 259.725

这个模型首先符合了经济意义的检验，同时在理论上通过方程的显著性检验，回归系数的显著性也都比较高，而且方程的拟合优度也很好。至于能不能用来解释因变量，还要接着进行其它检验。

（二）模型检验

1.多重共线性检验

多重共线性检验比较直观的是利用容忍度和方差膨胀因子，方差膨胀因子是容忍度的倒数，两者作用相同。容忍度的取值在0—1之间，越接近0表示多重共线性越强，越接近1表示多重共线性越弱；方差膨胀因子则一般以10为界限，大于10说明多重共线性越强。用这个标准分析表6数据，可见模型已经不存在较强的多重共线性，自变量之间线性关系较弱。

2.异方差检验

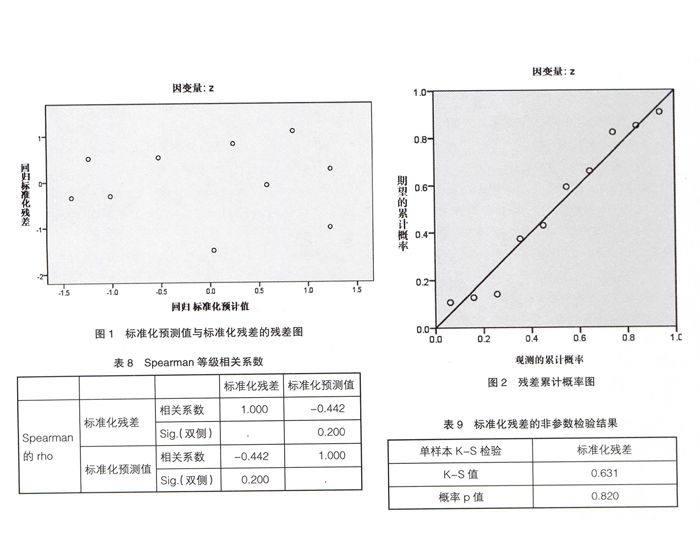
异方差一般通过绘制标准化预测值与标准化残差的残差图和计算它们之间的Spearman等级相关系数来检验。用SPSS软件分析以上得到的优化模型，得到图1和表8。

从图1可见，随标准化预测值的变化，标准化残差点在0线周围呈随机分布状态。从表8数据看，两者的Spearman等级相关系数为-0.442，且相应的检验统计量概率p值0.2大于0.05，因此拒绝原假设，认为该模型不存在异方差现象。

3.自相关分析

自相关性分析一般可做以时间为横坐标，残差为纵坐标的残差图，比较直观地观察看是否存在自相关，但一般不好把握。通过DW检验就可以比较准确地确定是否存在自相关了。查表，n=10，k=4，显著性水平为α=0.01，查表得：dL=0.340，dU=1.733。计算该模型的DW=1.976（见表7），满足dL=0.340≤1.733≤1.976≤2.267≤3.66=4-dL，可知优化模型不存在明显的自相关，即模型的随机扰动项互不相关。

4.零均值检验

零均值检验一般只是通过绘制标准化预测值与标准化残差的残差图来直观分析，看残差图中的点是否在以0线为中心的带状区域内随机散落来判断。从图1中大致可以看出，图中的点随机散落，可认为基本满足了零均值的假定。

5.正态性检验

对正态性假定的检验通过观察残差累计概率图中的点是否随机在零线周围分布和看标准化残差的非参数检验结果表中的概率p值是否满足要求。

从图2中可见，数据点在零线周围随机分布，并无规律可言，说明直观来看正态性较好；从表9中的概率p值就可肯定的判断出其大于0.05，标准化残差与标准正态分布不存在显著性差异，说明模型满足了正态性假定。

（三）模型的经济解释

1.科技活动人员对经济增长的影响

从建立的模型看，在其他条件不变的情况下，科技活动人员每增长0.483个百分点，工业总产值将平均增长1个百分点，即说明，科技活动人员数的增加将促进经济水平的增长，这是符合我们的经济理论及要求的。

2.除科技活动人员以外的从业人员对经济增长的影响

同理，在其他条件不变的情况下，除科技活动人员以外的从业人员数每增长1.005%，工业总产值将平均增长1%。与科技活动人员相比，除科技活动人员以外的从业人员对经济增长的贡献率更大一些。这与我国工业制造业粗放型增长方式为主的现状是相符的，同时这也从侧面说明了我国大中型企业提高技术因素贡献率的重要性。

3.科技活动经费支出对经济增长的影响

同理，在其他条件不变的情况下，科技活动经费支出每增长1.028个百分点，工业总产值将平均增长1个百分点。一方面，工业总产值与科技活动经费支出同方向变动；另一方面，相比于科技活动人员、除科技活动人员以外的从业人员两者对工业总产值的贡献率，科技活动经费支出的贡献率是更大的。

四、提高技术进步对经济增长贡献率的建议

（一）增加科技投入

科技投入是技术进步的基础，而我国的科技投入远远低于欧美国家，科研经费占GDP的比重远远低于发达国家，如2007年我国占1.4%，美国占2.68%，日本占3.44%。同时本文建立的多元分析模型说明，我国科技活动经费支出对经济增长的贡献率相对来说是很大的。因此，要使科技发挥充分作用，首先要增加科技投入；其次要建立一个适应经济发展的多渠道科技投入体系，切实使资金到位。第三，改变不合理的投入负担结构，促进企业技术推动力的发挥，变政府给企业科研经费为企业自留，自找科研经费，把企业特别是国有大中型企业真正推到科技开发、研究、推广和应用的第一线；第四，调整科技投入方向，要把资金的重点投向起点高又有带动性的“朝阳产业”和关键的技改和开发项目，特别是要通过大力发展高新技术产业，促进经济增长方式的转变。

（二）提高科技活动人员创造产值的能力

技术进步对经济发展发挥作用，其中最关键的因素是科技活动人员。这里的科技人员既应该包括专门从事科技研究与实验的人员，即R&D人员；也要包括专业技术人员。因此，要提高科技活动人员创造产值的能力，一方面要继续提高R&D人员的素质和创造力，加大高校和企业的教育培养力度；另一方面更加重视直接从事科技与经济结合工作的基层科技人员、职工的作用，提高他们应用先进技术作用于生产力的积极性和能力。

党的十七届五中全会通过的《中共中央关于制定国民经济和社会发展第十二个五年规划的建议》强调指出，推动中国经济发展要更多依靠科技创新驱动。“十二五”规划以科学发展为主题，以加快转变经济发展方式为主线。只有把科技进步和创新作为加快转变经济发展方式的重要支撑，集成创新和引进消化吸收再创新，不断深化政治、经济体制改革，不断深化教育、科技体制改革，才能驱动中国可持续发展。由此可见，“十二五”期间，国家将更加重视技术进步对经济增长的作用，采取措施提高我国的科技进步贡献率，实现我国经济的又好又快发展。●

【参考文献】

［1］董西明.科技进步对山东经济增长的贡献率分析［J］.工业技术经济，2006（1）.

［2］田茂峰.我国国民经济的柯布-道格拉斯生产函数的拟合分析［J］.中国水运，2007（6）.

［3］赵小芳，等.我国科技进步与区域经济发展的相关性分析［J］.科技进步与对策，2008（1）.

［4］齐微.柯布-道格拉斯（Cobb-Douglas）生产函数模型［EB/OL］.中国科技论文在线.http://www.paper.edu.cn.

［5］马岳红.R&D投入对中国高技术产业的影响——基于静态和动态的面板数据模型的实证研究［EB/OL］.中国科技论文在线.http://www.paper.edu.cn.

［6］郑念，张利梅.科普对经济增长贡献率的估算［J］.技术经济，2010（12）.

［7］李新运，于永信.21世纪初山东省经济增长对科技投入的需求分析［J］.科学与管理，1999（16）：13-16.

［8］王莹.关于科技进步与经济增长方式转变的思考［J］.商业研究，1999（8）：13-16.

［9］朱锋峰，贺德化，杜延军.国民经济增长中科技进步贡献率的计量分析［J］.华南理工大学学报，1998（6）：138-143.

［10］邓国华.科技进步贡献率的测定误区与实证分析［J］.当代财经，2001（2）：8-11.

［11］袁靖，胡磊.山东省科技进步贡献率测算的实证研究［J］.山东商业职业技术学院学报，2010（2）：90-93.