Mean Shift的渐进无偏变换图像配准

杨 烜

(深圳大学计算机与软件学院 深圳 518060)

1 引言

图像配准的目的是寻找两幅图像之间的变换函数，使得图像中相应目标的位置对准[1]。基于标志点对应关系的图像配准方法已得到广泛使用[2-6]，这类方法需要根据对应点对构造变换函数，变换函数具有明确的解析式，易于分析，计算简单。但这类变换函数往往是不可逆的，只能确保标志点之间的对应关系，不能保证图像间其他位置的对应关系，即变换的无偏性较差。

如果变换函数及其逆变换的Jacobia在1附近对称分布，称为无偏变换[7]。无偏变换对于图像配准非常重要，它意味着无论图像A向图像B配准，或是图像B向图像A配准都可以使同一目标得到配准。更重要的是，无偏变换是拓扑保持的，可以使图像在形变前后的拓扑关系不发生变化，这是大多数图像配准方法努力实现的目标[8-10]。目前关于无偏变换的研究比较少，文献[11]定义的对称代价函数，使源图像和目标图像互换后的变换函数互逆，但该方法采用FFD形变模型，计算量较大；文献[4]提出了标志点的一致性配准方法，该方法可以使标志点在正、反变换达到一致，但会导致标志点对应关系发生较大误差，还需要引入一致性强度配准进一步调整；文献[7]定义了变换函数与理想变换之间的对称KL距离，并定义了对称目标函数寻找无偏变换函数，但文献[7]采用的是粘性流体配准模型，计算量仍然很大。

本文针对基于标志点对应关系的图像配准问题，提出了一种基于无偏变换的渐进式图像配准方法，该方法只需要很少的几个初始标志点，通过不断加入新的标志点逐渐提高配准精度。本文从理论上分析了选择标志点的原则，利用Mean Shift迭代快速寻找对应标志点，构造无偏的变换函数。本文方法所构造的图像变换函数既具有较好的无偏特性，同时又保证了标志点之间的对应关系。

2 标志点分布对sKL距离的影响

无偏变换要求变换函数及其逆变换使图像被压缩和被膨胀程度是一致的，我们采用文献[7]提出的对称Kullback-Leibler(sKL)距离来描述变换的无偏性。假设变换函数为h，逆函数为h-1,h和h-1的Jacobi行列式分别为定义3种概 率 密 度 函 数 pdfh(ξ)=|Dh(ξ)|,pdfh-1(ξ)=|Dh-1(ξ)|,pdfid(ξ)=1，其中pdfid是单位映射(id(x)的概率密度函数。对称Kullback-Leibler(sKL)距离定义为

其中KL是Kullback-Leibler距离。寻找无偏的变换函数，就是使变换函数的sKL距离尽可能小。对于基于标志点对应关系的配准问题而言，就是寻找标志点对，在配准精度提高的同时，使变换函数的sKL距离尽可能小。

假设源、目标点集分别为P和Q，有N对标志点(pi,qi),i=1,2,…,N。pi∈P,qi∈Q，利用径向基函数构造变换函数，

其中x是变换空间中的点，R(r)是径向基函数，ri=||x-pi||，系数wi,i=1,…,N满足方程KW=Q-P,K是N×N矩阵，Kij=R(||pi-pj||)。径向基函数构造的h不能保证可逆，即使其逆函数h-1存在，h-1与h的压缩和膨胀程度也有较大差异，即无偏性较差。

下面我们将在一个简单2维模型上，分析添加标志点对变换函数sKL的影响。假设当前只有一个源标志点p向右水平移动到目标点q，水平位移量为d，变换函数h(x)及其Jacobi行列式Dh(x)为

当基函数是单调减的紧支撑径向基函数时，满足 ∂R(r)/ ∂r＜ 0 。不失一般性地以p为原点，则x＜ 0 的点(p左侧区域)Jacobi值大于1，而x＞0(p右侧区域)Jacobi值小于1。在点p的垂直上方L处添加点pa，该点水平位移至qa，假设位移量为dR( | |pa-p| | )+ε，其中dR( ||pa-p| |)是根据原变换函数h(x)对pa的位移量，ε是该位移的小扰动。则新的变换函数ha(x)为

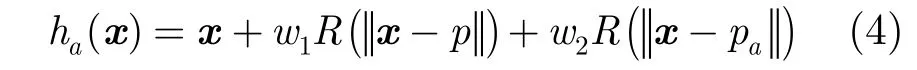
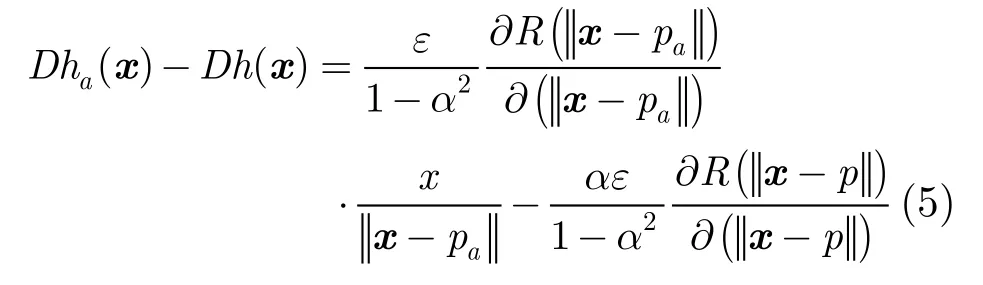
当L相对基函数的支撑集较小时，式(5)可以近似为

我们以紧支撑薄板样条(CSTPS)[5]作为径向基函数进行分析，可以推出

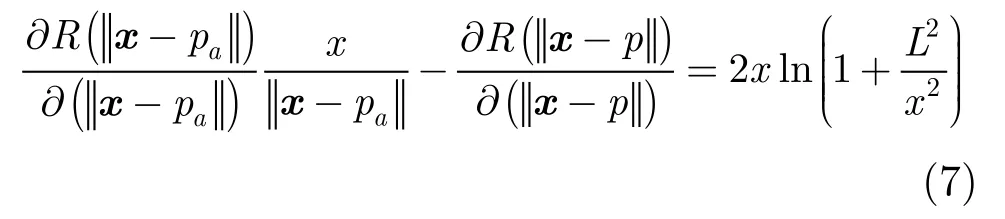
式(7)表明，新增点可以使x＞0的点Jacobi值增加，x＜0的 Jacobi值减小，这意味着通过添加点，在点p两侧的Jacobi值更接近1，即变换函数的无偏性改善了。需要说明的是，扰动ε不能过大，否则调整量会过大，可能会使变换函数的无偏性变差。上述分析中对于新增标志点pa的位置并没有严格的限制，一般地讲，我们需要在原标志点附近选择新增点，并且新增点的位移与原变换函数产生的位移是一致，即新加点的对应点选择在原变换函数的映射位置附近，这样该点的位移趋势与原变换函数近似，以满足ε较小的条件。另一方面，L较小也意味着将在较小的范围内搜索对应标志点，有利于寻找到准确的对应点。

对于图像配准问题，上述的要求可以这样理解：当原始变换函数的无偏性需要改善时，可以在原标志点的附近添加新增标志点，新增标志点的选择原则是以图像配准精度得到提高为依据，这样新增标志点可以对变换函数的无偏性起到改善作用。描述得更形象一些，当形变曲面被某些位移撕扯时，由于这种撕扯的受力不够均匀，会使图像在这些撕扯位置附近出现过度挤压或膨胀的情况。通过增加标志点，可以使撕扯效果得到缓解，变得平滑和均匀，变换函数的无偏性得到改善。

3 Mean Shift确定新增标志点对

假设S,R分别是源图像和参考图像，当前源标志点集为P，目标标志点集为Q，标志点对集合为∀pi∈P，选择新增源标志点满足

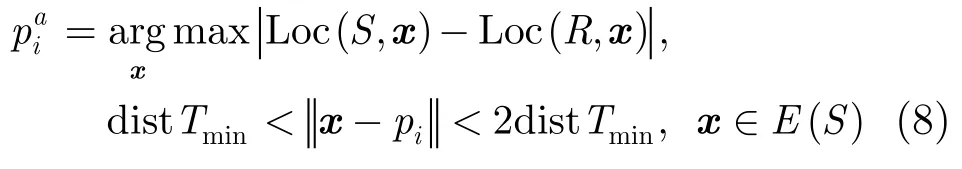
其中 L oc(I,x)是图像I中以x为中心的局部区域，E(S)是源图像S的边缘点集合。新增源标志点处于边缘上，其所处的区域与参考图像相差较大。同时该点与当前标志点的距离不能太远，这样可以利用当前标志点提供一个较理想的初始位置，有利于Mean Shift迭代收敛；同时也不能距离过近，以免局部形变受力不匀。

其中k(x)是核函数，分别是以为中心的邻域点，是归一距离，C和Cq是归一系数，u是灰度量化值，b(x)是量化函数，本文采用直方图模糊约束聚类方法进行量化。根据Mean Shift迭代，更新为

由于Mean Shift收敛是基于概率密度函数变化最大方向进行的，容易收敛于局部最优。需要对Mean Shift进行几点改进。首先进行多尺度配准，将配准图像下采样到大尺度图像上进行Mean Shift收敛，可以减小搜索范围。将大尺度图像的标志点对映射到小尺度图像中，得到粗配准结果。然后在小尺度图像中重复这个配准过程，得到精度更好的配准结果。

其次，由于Mean Shift统计的概率密度是不反映图像空间位置信息的，Mean Shift收敛后对应的点，可能并不是使局部图像空间对应关系最优的点。本文在Mean Shift迭代的路径中计算各点的局部配准度量，选择局部配准度量最大的点作为收敛结果，以提高对应点精度。另外，Mean Shift迭代路径要进行限制，以避免沿某个错误方向迭代过远。

在一个尺度下的完整配准过程如下：

步骤 1 输入源图像和参考图像，初始标志点对集合Ω，设置参数 d istThmin,Th，支撑集c。

步骤 2 利用式(2)计算Ω的变换函数h(x)。

步骤 3 如果 d istTmin＞T h，则算法退出，否则

步骤 4 ∀pi∈P，确定满足式(8)的新增源标志点。

步骤 7 计算Ω∪Ωa的变换函数ha(x)和，以及代价函数。

步骤 9 如果集合Ω没有增大，则 d istTmin=distTmin+ 1 。转至步骤3。

4 实验结果

分别针对大形变和小形变配准进行实验验证。图1中第1、第2行是Rose和Clown的大形变配准，分别选择了4个和7个初始标志点对，采用CSTPS作为径向基函数，支撑集c=200,d istTmin= 8,Th=16。图像大小均为 256×256，将图像下采样为128×128，进行大尺度配准，再进行小尺度配准。其中Rose图、Clown图中各添加了142, 92对标志点，可以看出， Rose的边界部分和Clown的帽沿这些形变剧烈的地方都得到了较好的配准。

为了比较配准效果，本文同时通过SIFT特征[13]确定对应标志点，将位移大于32的严重误配标志点对剔除。SIFT标志点对应关系的阈值设为使变换函数Jacobi值大于0的最大值，以尽可能多地保留标志点对。SIFT在Rose图和Clown图中分别添加了42和31对标志点，SIFT在Clown中寻找的标志点对存在误差，无法得到Jacobi值大于0的变换结果。这表明 SIFT不适用于形变比较剧烈的弹性配准问题，而本文方法具有较好的鲁棒性。

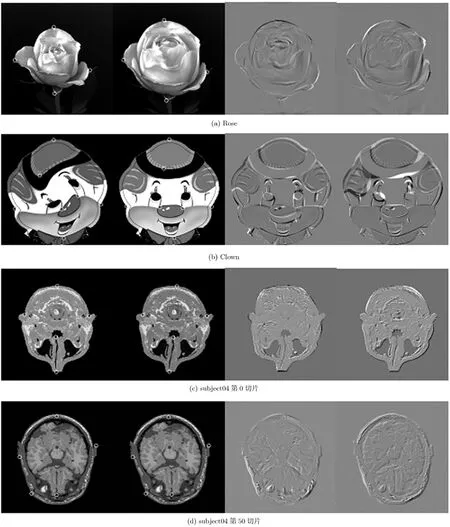
图1 将源图像配准到参考图像的实验结果(从左到右：待配图像，参考图像，本文方法配准结果与参考图像的差，SIFT配准结果与参考图像的差)

小形变配准采用了人体脑部扫描切片，待配准图像源于BrainWeb的subject04个体的脑部体数据切片，分别是第0和第50切片，经过人工小形变，得到参考图像。第0和第50切片中各选择了5对初始标志点。这两幅配准图像的细节比较丰富，特别是脑切片中部区域对配准要求较高，本文方法在第0，第50切片分别增加了110, 123对标志点，并且在脑中部区域确定了多个精度较高的标志点，提高了这些区域的配准精度，而SIFT在第0，第50切片中各新增65和308对标志点，但这些标志点中有许多点几乎重合，而在脑切片中部区域选择的标志点较少，分布也不均匀，导致这些区域配准精度不高。表1列出了本文方法和SIFT配准结果的互信息、均方差(MSD)、相关系数(CC)和sKL距离，加粗的数值表示最优结果。从表1可以看出，对于小形变配准问题，本文配准结果同样优于 SIFT方法的结果，同时sKL距离表明，本文方法得到的变换函数的无偏性优于SIFT方法。

5 结论

本文针对标志点对应关系的图像配准问题，提出了一种渐进式无偏变换的配准方法。首先人为选择数量极少的几个初始标志点，在初始标志点附近添加适当的标志点，利用Mean Shift迭代寻找相应的对应点；根据新标志点对判定配准度量的变化，确定需要添加到标志点集合的新标志点对；在扩展的标志点集合中继续利用Mean Shift迭代寻找对应标志点，逐步达到配准的效果。该方法中寻找对应标志点的过程充分考虑了变换无偏性的影响，同时为Mean Shift收敛提供了较准确的初始位置，多尺度的配准策略有利于鲁棒地寻找到准确的对应点。实验比较结果表明本文方法不仅适用于大形变配准问题，也可以用于解决小形变问题，是一种鲁棒的配准方法。

表1 配准结果比较(N/A表示变换函数拓扑不能保持)

[1]Rueckert D and Aljabar P. Nonrigid registration of medical images: theory, methods, and applications.IEEE Signal Processing Magazine, 2010, 27(4): 113-119.

[2]Myronenko A and Song X B.Intensity-based image registration by minimizing residual complexity.IEEE Transactions on Medical Imaging, 2010, 29(11): 1882-1891.

[3]Chen J, Tian J, Lee N,et al.. A partial intensity invariant feature descriptor for multimodal retinal image registration.IEEE Transactions on Biomedical Engineering, 2010, 57(7):1707-1718.

[4]Johnson H J and Christensen G E. Consistent landmark and intensity-based image registration.IEEE Transactions on Medical Imaging, 2002, 21(5): 450-461.

[5]Zhang Z X and Yang X. Elastic image warping using a new radial basic function with compact support. Proceedings of International Conference on Bio-inspired Systems and Signal Processing 2008, Funchal, Madeira, Portugal, January 28-31,2008: 216-219.

[6]Shen D and Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration.IEEE Transactions on Medical Imaging, 2002, 21(11): 1421-1439.

[7]Leow A D, Yanovsky I, Chiang M C,et al.. Statistical properties of Jacobian maps and the realization of unbiased large-deformation nonlinear image registration, 2007, 26(6):822-832.

[8]Lin X B, Qiu T S, Morain-Nicolier F,et al.. A topology preserving non-rigid registration algorithm with integration shape knowledge to segment brain subcortical structures from MRI images.Pattern Recognition, 2010, 43(7):2418-2427.

[9]Sdika M. A fast nonrigid image registration with constraints on the Jacobian using large scale constrained optimization.IEEE Transactions on Medical Imaging, 2008, 27(2): 271-281.

[10]Noblet V, Heinrich C, Heitz F,et al.. 3-D deformable image registration: a topology preservation scheme based on hierarchical deformation models and interval analysis optimization.IEEE Transactions on Image Processing, 2005,14(5): 553-566.

[11]Gholipour A, Kehtarnavaz N, Yousefi S,et al.. Symmetric deformable image registration via optimization of information theoretic measures.Image and Vision Computing,2010, 28(6): 965-975.

[12]Comaniciu D, Ramesh V, and Meer P. Real-time tracking of non-rigid objects using mean shift. Proceedings of IEEE Conference Computer Vision and Pattern Recognition, Los Alamitos: IEEE Computer Society Press, 2000: 142-149.

[13]Lowe D G. Distinctive image features from scale-invariant keypoints.International Journal of Computer Vision, 2004,60(2): 91-110.