基于MRAS和SMO相结合的PMSM矢量控制

李晓宁，刘晨程，李卫东

（电子科技大学 机械电子工程学院，四川 成都 611731）

基于MRAS和SMO相结合的PMSM矢量控制

李晓宁，刘晨程，李卫东

（电子科技大学 机械电子工程学院，四川 成都 611731）

通过对MRAS和SMO进行分析，提出了一种基于MRAS和SMO相结合的永磁同步电机无速度传感器的控制方法。由SMO算法实现永磁同步电机定子电流的估计，构成MRAS算法的可调模型部分，实现了永磁同步电机转子转速的估计和整个系统的三闭环控制，详细介绍了基于MRAS和SMO相结合的永磁同步电机无速度传感器控制系统的建立并进行了测试。测试结果表明，该控制系统具有良好的低速调速功能、动静态性能和鲁棒性。

永磁同步电机；无速度传感器；模型参考自适应系统；滑模观测器

1 引言

永磁同步电机具有高转矩惯性比、高能量和高效率等优点，近年来在航空航天、工业控制等领域得到了广泛的应用，然而在高性能永磁同步电机控制系统中，一般通过在转子轴上安装机械式传感器来测量电机的速度和位置，以实现高性能的位置闭环控制，但是机械传感器存在成本高，安装困难，接线多，易受环境影响等缺点。因此，国内外学者提出各种无速度传感器的控制方案来克服机械传感器的缺点。永磁同步电机无速度传感器控制系统通过测量电机定子电流和电压算出转子位置替代了传统的机械位置传感器且系统成本低、可靠性较高。其中较为成熟的有MRAS和SMO算法。MRAS模型精确，但易受参数变化的影响，而SMO对参数变化不敏感，鲁棒性强且动态响应快，但是SMO的低速时估计精度不高。因此，将MRAS和SMO相结合，用SMO构成MRAS的可调模型，可以克服MRAS对参数变化的敏感和SMO低速时的估计不精确的缺点。

本文将针对基于MRAS和SMO相结合的永磁同步电机无速度传感器的控制系统，着重介绍了MRAS和SMO相结合的数学模型，并对测试结果进行了详细的分析。

2 PMSM数学模型分析

通过坐标变换对永磁同步电机实现磁场矢量控制，能获得较好的动态和稳态特性，并通过调节PID参数能获得更好的性能。

2.1 PMSM在旋转坐标系下的模型［1］

在永磁同步电机中，取永磁体基波励磁轴线（磁极轴线）为d轴（直轴），顺着转子旋转方向超前d轴90°（电角度）为q轴（交轴），dq轴系以电角度ωr随同转子一道旋转，它的空间坐标以d轴与A轴间的电角度θr来确定。于是永磁同步电机在dq坐标系下的数学模型可以表示为

电压方程：

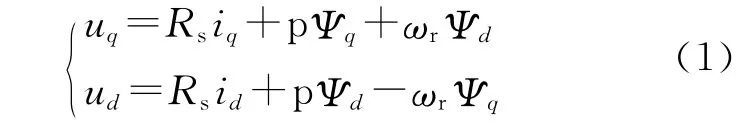
磁链方程：

2.2 PMSM在静止坐标系下的模型［1］

以永磁同步电机的三相ABC轴系为参考，取A轴为D轴，超前D轴90°（电角度）方向为Q轴，它是同三相ABC轴静止的，在满足磁通不变的情况下永磁同步电机在DQ坐标系下的数学模型为

电压方程：

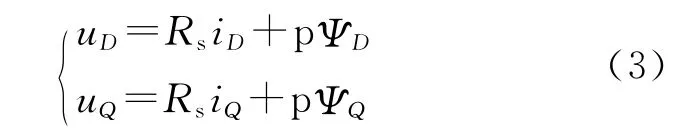
式中：uD，uQ为D，Q轴定子电压；iD，iQ为D，Q轴定子电流；ΨD，ΨQ为D，Q轴磁链。

3 MRAS和SMO算法分析

MRAS是基于参考模型和可调模型来实现速度辨识，但是参考模型本身的参数准确程度直接影响速度辨识的精度。滑模观测器法是一种闭环观测器方法，它采用估计偏差来确定滑模控制机构，并使控制系统的状态最终稳定在设计好的滑模超平面上。

3.1 MRAS算法分析［2］

MRAS的主要思想是将含有待估计参数的方程作为可调模型，将不含未知参数的方程作为参考模型，2个模型具有相同物理意义的输出量。

在永磁同步电机中建立以定子电流为状态矢量的 MRAS模型，由式（1）、式（2）可得：

对式（5）进行简化，令：

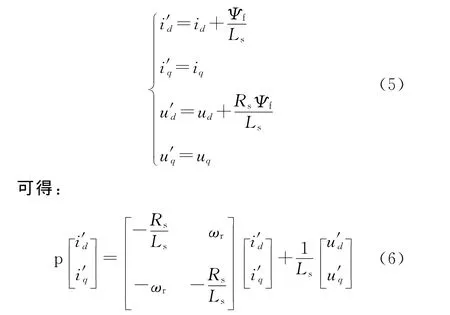
式（6）确定为MRAS模型中的参考模型。

式（6）以估计值表示可得：

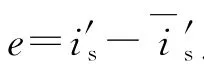
式（8）为定子电流矢量误差方程，由方程可得一个标准的反馈系统，为使反馈系统稳定，根据波波夫超稳定理论［1］可得：

式中：带有“-”为估计值。

由式（6）～式（9）可以确立MRAS的模型。

3.2 SMO算法分析

由于SMO对参数变化不敏感，对外部扰动的鲁棒性强且动态响应快。滑模控制的基本原理［3］是通过切换函数实现的，切换函数可以根据控制的需要来选择，它是系统状态变量的函数，当输出随着系统状态变化即不稳定时，滑模控制器会相应的把输入函数的这一状态切换到另一状态，使系统的状态能在有限的时间内回到开关平面，并沿着开关平面滑动。在永磁同步电机中，由式（3）可知，在静止DQ坐标中定子电压方程为

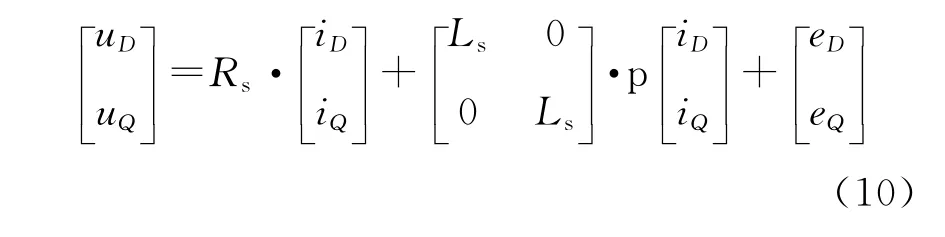
其中eD，eQ为励磁磁通产生的感应电动势，即有：

由式（11）可得滑模观测器方程为

式中：K为观测器开关增益。

将式（10）和式（12）相减可得：

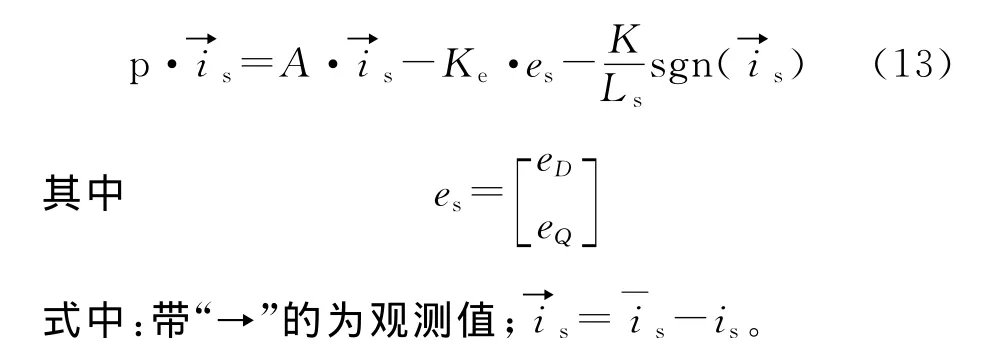
式（13）为滑模观测器的误差动态方程，为使得式（13）是渐近稳定的，则应该满足条件：

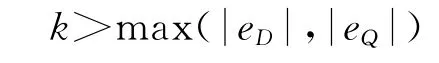
联合式（11）、式（13）可得：

4 PMSM矢量控制系统的构建

对MRAS系统进行变结构，即通过滑模观测器对电流的估计代替原系统中的可调模型，是为了更好的对速度进行跟踪，提高动静态特性。

4.1 MRAS和SMO相结合的模型构建

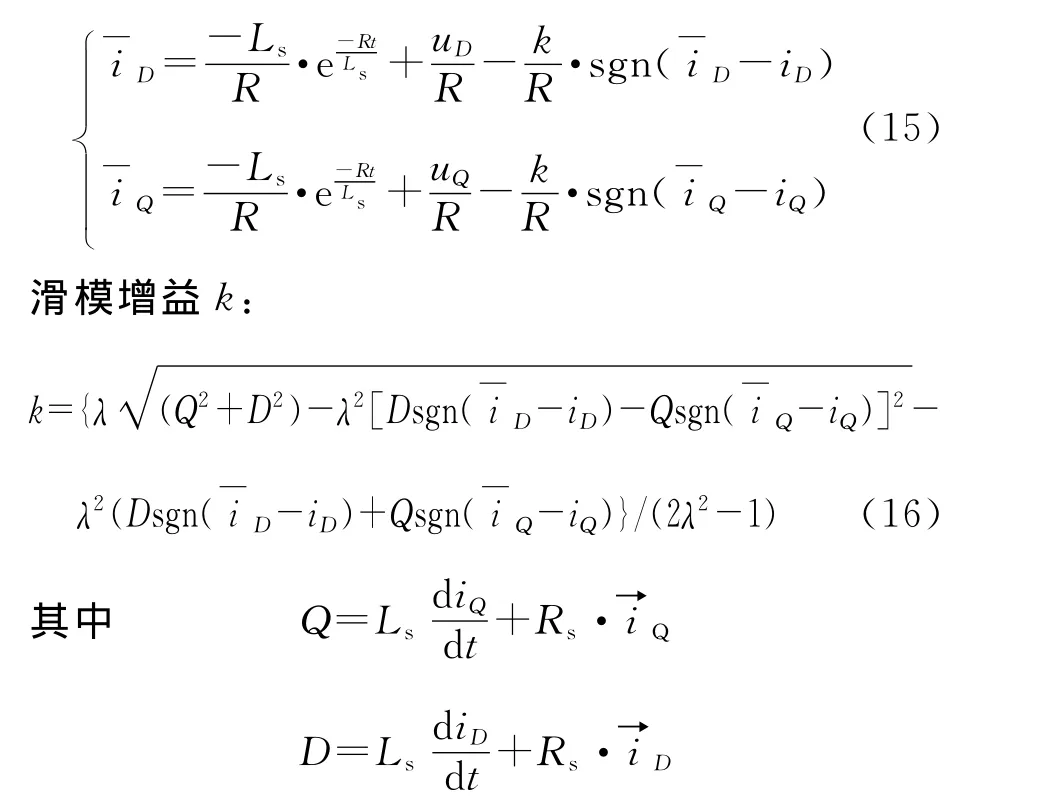
将式（15）变换到旋转坐标轴上可得：

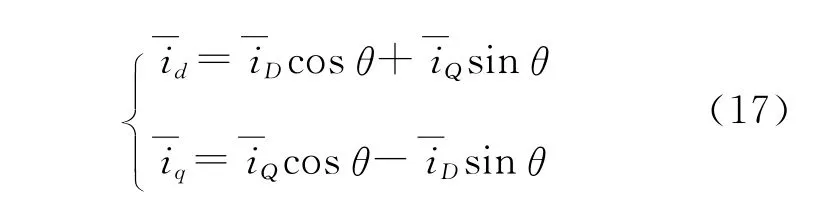
MRAS模型是通过定子电流来估计转速、确定自适应律，整个系统满足波波夫超稳定方程，转速误差信息是i′s×i-s，因此将式（17）代入可调模型替代原系统中的式（7），系统同样满足波波夫超稳性定理，即系统稳定。联合式（5）、式（9）、式（17）可得：

由式（18）可以构建出变结构的MRAS模型，如图1所示，图1中us，is是旋转坐标轴中定子电压、电流，us，is是静止坐标中的定子电压、电流。

图1 MRAS和SMO相结合模型Fig.1 Model of combination MRAS and SMO

4.2 永磁同步电机的控制系统构建［4-6］

本文中永磁同步电机的控制系统包括Clark模块、Park模块、Ipark模块、PID模块、PWM 驱动模块、空间矢量SVPWM模块、无速度传感器模块、电压电流检测模块，系统框图如图2所示。

图2 永磁同步电机的控制系统Fig.2 The control system of PMSM

5 测试结果分析［7］

本文在硬件平台上通过CCS开发环境建立了基于MRAS和SMO相结合的永磁同步电机的矢量控制系统并进行了测试，其中永磁同步电机参数如下：R＝5.58Ω，ne＝3 000r／min，J＝0.3 kg·cm2，Ld＝Lq＝17.33mH。

对文中的辨识方案［7］进行测试可得在CCS开发环境中实时数据曲线，图3～图8给出了电机从静止启动到不同转速时的启动过程。测试是在空载情况下进行的，其中电流估计值是＿IQ10（）定点数即放大1 024倍。由图3～图8可知，系统能够很好地跟着实际速度，在低速时超调量基本上为0，响应时间很短，误差基本上为0，有很好的动态性能；在高速时，超调量较小约为15%，响应时间较短，在稳定后误差基本上为0，也有很好的动态性能。相比基于MRAS或SMO的无速度传感器的控制系统，本系统不仅在高转速时也能很好地实现速度估计，在低转速时速度估计更好。

由图8可知，电机从8r／min突变到1 500 r／min时，超调量较小约为13.5%，响应时间约为4.5s，稳定后误差基本上为0，体现出了系统很好的动态性能和鲁棒性。

图3 转速为8r／min时的速度估计值Fig.3 Speed estimation about 8r／min

图4 转速为8r／min时旋转D轴的电流估计值Fig.4 The Daxis current estimate about 8r／min

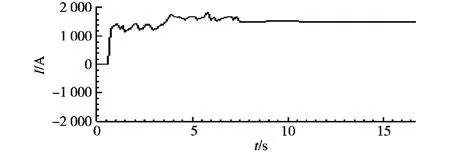
图5 转速为8r／min时旋转Q轴的电流估计值Fig.5 The Qaxis current estimate about 8r／min

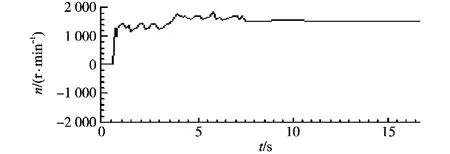
图6 转速为1 500r／min时的速度估计值Fig.6 Speed estimation about 1 500r／min

图7 转速为1 500r／min时旋转D轴的电流估计值Fig.7 The Daxis current estimate about 1 500r／min

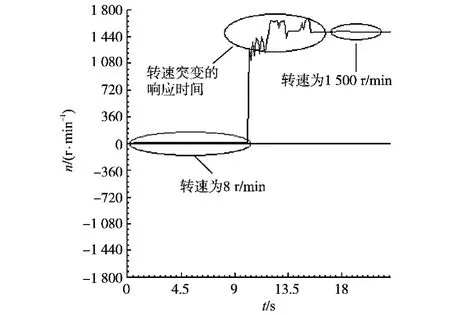
图8 转速从8r／min突变到1 500r／min时的速度估计值Fig.8 The speed estimate when the speed changing from 8r／min to 1 500r／min

6 结论

基于MRAS和SMO相结合的控制系统相对于单独的MRAS或SMO控制系统而言，在电流估计时受参数变化的影响较小，在估计转速时通过与精确的MRAS中参考模型的转速信息误差来估计的，因此在低速时电流的估计精度，动静态性能和鲁棒性方面有很大的提高。

［1］ 王成元，夏加宽.电机现代控制技术［M］.北京：机械工业出版社，2006.

［2］ 王庆龙，张崇巍，张兴.基于变结构 MRAS辨识转速永磁同步电机矢量控制系统［J］.系统仿真学报，2007，19（22）：5230-5233.

［3］ 马靖颖，汤宁平.用于PMSM无位置传感器控制的滑模观测器的设计与仿真［J］.防爆电机，2009，44（151）：31-34.

［4］ 王君艳.交流调速［M］.北京：高等教育出版社，2006.

［5］ 邱佰平，凌云.基于 MRAS的新型永磁同步电机的速度辨识方案［J］.机电工程技术，2009，38（10）：32-35.

［6］ 齐放.永磁同步电机无速度传感器技术的研究［D］.南京：南京航空航天大学，2007.

［7］ Texas Instruments.Digital Motor Control［EB／OL］.http：／／focus.ti.com／lit／ug／spru485a／spru485a.pdf

［8］ 苏奎峰，吕强，耿庆锋，等.TMS320F2812原理与开发［M］.北京：电子工业出版社，2005.

修改稿日期：2012-02-03

Vector Control Method of PMSM Based on Combining MRAS and SMO

LI Xiao-ning，LIU Chen-cheng，LI Wei-dong

（SchoolofMechanicalandElectricalEngineering，UniversityofElectronicScienceand Technology，Chengdu611731，Sichuan，China）

From the anlysis of MRAS and SMO，a control method based on PMSM which is a combination of MRAS and SMO was proposed.The estimation of stator current is realized by SMO method which is composed of the adjustable model of MRAS method and realized the estimation of the rotor speed as well as the three close-loop feedback control of the whole system.How to build a speed sensorless control system of PMSM was illustrated based on the combination of MRAS and SMO and tested it.The test turned out that this control system have a good low speed adjustment and dynamic performance and robustness.

permanent magnet synchronous motor；speed sensorless；model reference adaptive control system；sliding mode observer

TM351

A

国家自然科学基金（60971037）

李晓宁（1972-），男，博士，硕士导师，高级工程师，Email：lixn＿uestc＠163.com

2011-05-30