高拱坝安全度计算方法对比分析

宋 鹏 ， 程 琳 ， 田振华

（1.河海大学水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学水资源高效利用与工程安全国家工程研究中心，江苏 南京 210098；3.河海大学水利水电学院，江苏 南京 210098）

0 引 言

拱坝与坝基整体失稳机理分析成果表明，拱坝的可能破坏形式有坝体本身的强度破坏、拱坝坝体的屈曲、拱坝沿建基面的滑移、坝肩岩体的滑移和坝肩岩体过大的压缩变形[1]。从已建拱坝来看，影响拱坝整体安全最主要的因素为坝肩岩体的稳定性。目前，常用有限元法计算拱坝的整体安全系数，主要有超载法、强度储备法和综合法，失稳判据有塑性区贯通判据、位移突变判据和屈服体积比突变判据。不同的模拟破坏方式其计算结果有何不同，分析计算时如何根据各自的特点进行选择；不同的失稳判据各有什么优势和不足，具体采用哪种判据相对更为合理，是用有限元法评价拱坝整体安全度时存在的关键问题。为此，本文结合实际工程，对3种计算方法和3种失稳判据进行了比较，考察各自的失稳特点，探讨了其适用性。

1 工程实例

1.1 工程概况

某拱坝为混凝土双曲拱坝，坝顶高程1 885 m，坝底高程1 580 m，正常蓄水位1 880 m。两岸基岩受构造影响强烈，断层、层间挤压错动带、节理裂隙等各类结构面发育。左岸存在f5、f2断层：f5贯穿分布于坝址左岸山体内，产状N35°～45°E，SE∠70°～80°；f2发育在 1 650～1 700 m大理岩中， 产状N30°～40°E， NW∠40°～56°。 f13、 f14断层贯穿分布于右岸山体内， 产状分别为 N50°E， SE∠70°； N52°E， SE∠65°～70°。

1.2 模型建立

选取坝体和一定范围的基岩建立三维有限元模型，边界范围为：以坝轴线为中心，上游侧取1倍坝高，下游侧取1.5倍坝高，坝肩向两岸各延伸1倍坝高，坝基以下取1倍坝高。对铅直基础边界按法向链杆模拟，底部水平基础边界施加全部位移约束，顶部为自由边界。模型充分考虑了坝体的结构特点、河谷地形地貌，模拟了坝肩开挖槽，左岸f5、f2及右岸f13、f14断层，深部裂隙以及坝区分布的各种岩体。单元主要采用六面体8节点等参单元。模型共计137 543个单元，145 812个节点。图1为坝体及坝基的整体有限元模型。采用Druker—Prager屈服准则[2]进行弹塑性分析。荷载组合为：上游正常蓄水位+相应下游水位+坝体自重+淤沙压力+温降。

图1 拱坝有限元模型

2 计算结果

2.1 超载法

按照超容重的方式对模型进行超载，超载系数Kp从1开始，以后逐级增加。分别依据塑性区贯通判据、位移突变判据、屈服体积比突变判据分析拱坝的整体安全系数。

2.1.1 塑性区

图2为Kp为2和3.5时坝体与坝基的等效塑性应变区域分布图。图中黑色区域为等效塑性应变大于10-4的区域。从图2可知：

（1）坝体。Kp=1时，坝体屈服范围极小，只有坝踵受拉屈服和坝趾受压屈服；Kp=2时，屈服范围显著增大，上游坝面两侧拱端中下部受拉屈服，上层拱圈中间部位受压屈服。同时，下游坝面周边区域受压屈服；随着超载的继续，塑性区发展迅速，至Kp=3.5时，整个坝体几乎全部屈服，上游坝面主要受压，下游坝面主要受拉。

（2）坝基。Kp=1时，在坝踵和坝趾部位基础出现小范围的屈服区；Kp=2时，拱坝底部基岩开始局部屈服连通，并沿岸坡向上部高程延伸；至Kp=3.5时，左岸基础已经明显屈服贯通，形成向下游河床的滑移通道。

图2 坝体及基岩塑性区分布

2.1.2 位移

考察拱坝左岸1/4拱圈坝顶、拱冠梁坝顶以及右岸1/4拱圈坝顶点的顺河向位移随超载系数的变化。图3为坝顶顺河向位移与超载系数的关系。由图3可知，Kp＝3.5时，左岸1/4拱圈和拱冠梁坝顶点顺河向位移产生突变； Kp=4时，右岸1/4拱圈坝顶点顺河向位移产生突变。

2.1.3 屈服体积比

图4为屈服体积比随超载系数的变化曲线。由图4可知，屈服体积比在Kp=3.5时产生突变。

图3 坝顶顺河向位移与超载系数关系

图4 屈服体积比与超载系数关系

2.2 强度储备法

应用强度储备法计算时，等比例降低坝基岩体材料的抗剪强度，折减系数Kc取值从1开始，以后逐渐增大。

2.2.1 塑性区

Kc=2和4时，坝体与坝基的等效塑性应变区域分布见图5。从图5可知：

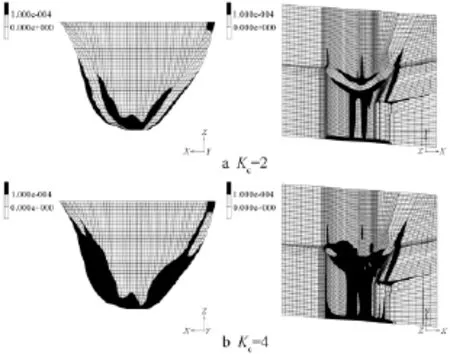
图5 坝体及基岩塑性区分布

（1）坝体。Kc=2时，上游坝面两侧拱端中下部受拉屈服，下游坝面低高程拱端局部受压屈服；随着坝基岩体强度的降低，上、下游坝面的屈服区由下部向上部延伸，并沿坝厚方向向内层扩展。至Kc=4时，坝体中部以下拱端已全部屈服连通，靠近上游坝面部位主要受拉，靠近下游坝面部位主要受压。此外，坝体的绝大部分区域尚未产生屈服。

（2）坝基。Kc=2时，坝踵和坝趾部位基础出现带状屈服区；此后，屈服区在拱坝底部基岩开始局部贯通，并沿岸坡向上部高程延伸。Kc=4时，左坝肩中部以下岩体全部屈服连通。

2.2.2 位移

图6为左岸1/4拱圈坝顶、拱冠梁坝顶以及右岸1/4拱圈坝顶点顺河向位移与折减系数的关系。由图6可知，左岸1/4拱圈坝顶点顺河向位移在Kc=3时产生突变，拱冠梁坝顶点顺河向位移在Kc=5时产生突变；右岸1/4拱圈坝顶点顺河向位移在Kc=6时产生突变。

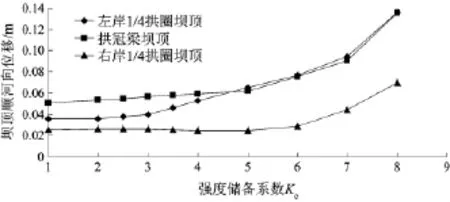
图6 坝顶顺河向位移与强度储备系数关系

2.2.3 屈服体积比

图7为屈服体积比随折减系数的变化。由图7可知，屈服体积比在折减系数Kc＜4时增长缓慢，在Kc＞4 时迅速增大。

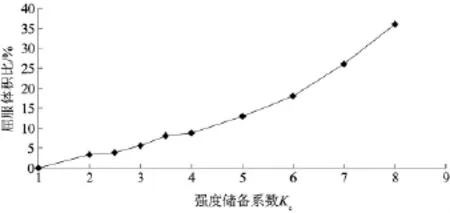
图7 屈服体积比与强度储备系数关系

2.3 综合法

采取先降强后超载的方式。首先，将岩体的材料参数按等比例降低30%，即选取Kc=1.3。在此基础上，Kp从1开始逐级增大，直至结构整体失稳。

2.3.1 塑性区

Kp=1和3时，坝体与坝基的等效塑性应变区域分布见图8。坝体和坝基塑性区的扩展情况与超载法分析时极为相似。当Kc=1.3、Kp=3时，左岸坝肩岩体全部屈服贯通，形成向下游河床的滑移通道。

2.3.2 位移

图9为左岸1/4拱圈坝顶、拱冠梁坝顶以及右岸1/4拱圈坝顶点顺河向位移与超载系数的关系。由图9可知，Kp＝2.5时，左岸1/4拱圈和拱冠梁坝顶点顺河向位移产生突变；Kp=3时，右岸1/4拱圈坝顶点顺河向位移产生突变。

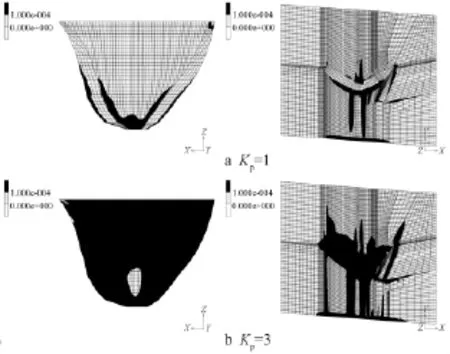
图8 坝体及基岩塑性区分布

图9 坝顶顺河向位移与超载系数关系

2.3.3 屈服体积比

图10为屈服体积比随超载系数的变化曲线。由图10可知，曲线在Kp＝3时出现拐点，以后屈服体积比显著增大。

图10 屈服体积比与超载系数关系

3 成果分析

按照超载法、强度储备法、综合法分析并分别以塑性区贯通判据、位移突变判据、屈服体积比突变判据作为失稳判据的拱坝整体安全系数见表1。从表1可以看出：

（1）同一种计算方法在按照不同失稳判据评价拱坝整体安全度时所得结果是不一致的。同样，选择统一的失稳判据，应用不同的安全度计算方法所得结果也不尽相同。

表1 不同方法计算所得拱坝整体安全系数

（2）超载法与强度储备法分析所得拱坝坝体及坝肩岩体的破坏模式不同。按照超载法计算，拱坝失稳时，整个坝体几乎全部屈服，坝顶高程以下的左岸坝肩基岩全部屈服贯通。而采用强度储备法计算，拱坝失稳的临界状态时，坝体只有中部以下拱端局部屈服，坝肩岩体也只在左岸中部以下屈服贯通。产生的原因是：应用超载法计算时，坝体的局部屈服破坏导致坝体应力的重分布，提高了坝体未屈服部位的应力状态。超载过程中，增加的水压荷载绝大部分由这些未屈服部分来承担，使其应力状态进一步提高。过高的应力状态使坝体未屈服的部位逐渐屈服，最终导致整个坝体的屈服破坏。同时，增大的水压荷载通过坝体传至坝肩岩体，使基岩的应力场发生很大变化，较低部位基岩承受的荷载较大首先屈服。随着超载的继续，较高部位的岩体也逐渐受压屈服，最终形成连通的屈服区域。采用强度储备法时，坝体承受的水压荷载不变，岩体材料参数的降低对坝体的应力状态有一定的影响，但程度并不很大。拱坝的整体失稳主要受基岩材料强度的影响，较差的岩体对强度的折减反映较为敏感，随着材料参数的降低，相对薄弱部位的岩体首先屈服软化，决定了拱坝最终的失稳形式。

（3）综合法的失稳模式取决于超载与降强的组合形式，与主要的破坏模拟方式计算结果接近。本文采取先降强后超载的方式，则综合法最终的破坏模式与超载法相似。

（4）超载法计算方法比较简单，通用性较强；强度储备法能比较充分地反映坝肩不良地质构造和岩体性质对坝体安全的影响，适用于基岩软弱结构面发育且岩性较差的工程；采用综合法时，应根据工程的具体地质情况和结构特点选择先超载后降强或先降强后超载的组合方式。

（5）采用塑性区贯通判据评价拱坝整体安全度时，塑性贯通率和失稳临界状态无明确的对应关系，只能根据经验进行判断，增加了人为因素的干扰。

（6）位移突变判据与失稳控制点的选择关系密切。3种模拟破坏均表现为左岸1/4拱圈坝顶点比右岸1/4拱圈坝顶点的安全系数小。在按照强度储备法计算时，拱坝整体安全系数从左岸到右岸依次增大。这是因为左岸的基础刚度小于右岸，坝体靠近左岸的部位比靠近右岸的部位先失稳。采用位移突变判据作为失稳判据，分别按3种破坏模拟方式计算拱坝整体安全度，基础刚度的不对称性在应用折减系数法计算时表现的最为敏感。在采用位移突变判据时，坝体最先失稳的部位难以确定，给控制点的选择带来一定的困难，分析结果存在不确定性。

（7）屈服体积比突变判据以坝体及坝基系统的屈服体积为考察对象，受局部材料的强度和结构影响较小，避免了塑性区贯通判据尚无评判失稳的客观指标以及位移突变判据控制点选择的问题。屈服体积比为单值标量，用其突变作为评价拱坝整体安全度的依据，结果惟一，便于分析和应用。

［1］ 董玉文，任青文.高拱坝稳定安全度研究综述［J］.水利水电科技进展， 2006， 26（5）:78-82.

［2］ 徐干成，郑颖人.岩土工程中屈服准则应用的研究［J］.岩土工程学报，1990，12（2）:93-99.