混凝土坝应力应变监控指标研究

杨 健，牛春功

（1.中国水电工程顾问集团公司，北京 100120；2.中水东北勘测设计研究有限责任公司，吉林 长春 130021）

0 引 言

应力应变是混凝土大坝的主要安全监测项目之一，制定科学合理的混凝土大坝应力应变监控指标，对准确识别险情、保障大坝安全具有重要意义，是实现大坝安全运行的关键。拟定安全监控指标的主要任务是根据大坝和坝基抵御经历荷载的能力，来评估和预测抵御可能发生荷载的能力，从而确定该荷载组合下监控效应量的警戒值和极值。由于大坝失事为小概率大损失事件，破坏实例少，且破坏时往往伴随着突发性灾难，无法搜集到完整的数据信息；有些大坝可能还没有遭遇最不利荷载；随着时间的推移，坝体材料渐趋老化，大坝和坝基抵御荷载的能力也在逐渐变化。因此，安全监控指标的拟定是一个相当复杂的问题，也是国内外坝工界研究的重要课题[1-2]。通常在采用典型小概率法拟定监控指标时，都是将实测数据套到一个常用的较为合适的理论分布函数上，带有一定的人为因素。本文首先阐述基于应变计实测资料的应力转换方法，进而运用遗传算法优化的最大熵原理，无需事先假设分布类型，直接根据各基本随机变量的数字特征值进行计算，拟定应力应变监控指标。

1 实测应变值应力计算

在实测应变和徐变试验资料的条件下，采用变形法计算各个方向混凝土的正应力。基本原理如下[3-4]：

计算实测应变资料，绘制成单轴应变过程线，将全部应变过程划分为几个时段，时段是不等间距的。早期应力增量较大，时段细些；后期应力变化不大，可以将时段划分得粗些。将徐变增量进行计算，按每一时段的开始龄期τ0，τ1，…，τn-1绘制成总变形过程线。变形法计算应力原理见图1。图中，E（τ）为τ时刻混凝土的瞬时弹性模数。

徐变变形为随加荷时间持续而增长的变形。因此，某一时刻的实测应变不仅有该时刻弹性应力增量引起的弹性应变，还包含在此以前所有应力引起的总变形。τi-1～τi时段应力增量Δσi引起的总变形，将包含在 τn-1～τn时段的应变中。因此，计算这一时段的应变增量时应扣除该分量。

图1 变形法计算应力原理

在计算时段之前的总变形影响值称之为 “承前应变”，用ε表示，其值为

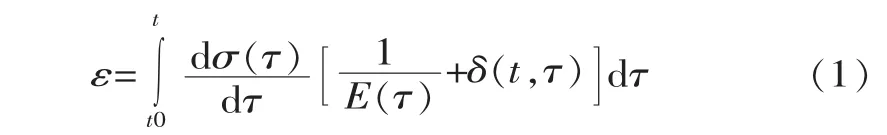
上述是计算承前应变的数学表达式，实际上是用下面的近似式计算

2 遗传算法优化的最大熵监控指标拟定

信息熵实质上都表示系统的随机性和无序程度[5-6]，可用系统的概率分布函数的泛函表示

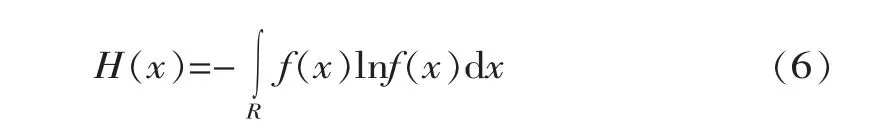
式中，f（x）为连续型随机变量x的分布密度函数；R为积分区间。

根据最大熵原理可知，最小偏差的概率分布是使熵H（x）在根据已知样本数据信息的一些约束条件下达到最大值的分布，即

约束条件

式中，μi为随机变量的i阶原点矩。

通过调整f（x）来使得熵H（x）达到最大值。采用拉格朗日乘子法来解决此问题。建立如下拉格朗日函数

式中， λi（i=0，1，…，n）为拉格朗日系数， 即拉格朗日乘子。

在得到各个系数的具体值后，代入概率密度函数f（x）中。令xm为监测效应量的极值，当x≥xm时，大坝将要出现异常或险情，其概率为

式中，α为显著性水平，根据大坝重要性来确定。

由式（11）可以反推求出大坝监测效应量的极值，此即为大坝监控指标。

图2 遗传算法优化拉格朗日系数流程

3 工程实例

某高拱坝属大 （1）型一等工程，永久性主要水工建筑物为1级建筑物。水库正常蓄水位1 240 m，设计洪水位1 238.10 m，校核洪水位1 243.00 m，死水位1 166.00 m。根据双曲拱坝受力特点，大坝应力应变布置为 5拱 （1 000、1 050、1 100、1 150 m和1 190 m高程）5梁 （9、15、22、29号和35号坝段）监测系统。大坝共进行了4次蓄水。2010年7月16日，水库开始第3阶段蓄水；2010年10月22日，库水位达到工程蓄水以来最高水位1210.58 m；其后，水位开始缓慢消落；2011年6月13日，坝前水位逐步上升，开始第4阶段蓄水。本文分析时段从2010年7月下闸蓄水至今。

该拱坝目前正处于蓄水期，故选取坝踵垂向正应力的每个月的最大值作为研究样本。通过计算，河床坝段 （22号坝段）坝踵9向应变计组A22-S9-01的计算结果见图3。从图3可知，拱圈切向当前应力为－2.816 9 MPa，拱圈径向为－4.270 8 MPa，垂直向为－6.841 89 MPa。

图3 22号坝段坝踵A22-S9-01测点正应力过程线

根据以上样本，运用本文所述的方法按2阶计算得到的拉格朗日系数分别是λ0=-244.995、λ1=-67.606和λ2=-4.660，其遗传算法迭代进化过程见图4。 最大熵概率密度函数为f（x）=e-244.995-67.606x-4.66x2。与正态分布相比，运用最大熵确定的分布避免了人为假定的缺陷，具体的密度函数见图5。

图4 遗传算法优化系数迭代过程

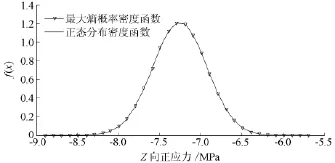
图5 概率密度函数对比

取显著性水平α=0.05时，大坝坝踵垂直向正应力在蓄水期出现早期险情，需要及时甄别和处理。此时，垂直向正应力预警值为－6.714 7 MPa，比该值更大时，大坝坝踵垂直向正应力在蓄水期出现早期险情，需要及时分析研究其成因，尽快排除险情。

4 结 语

应力计算采用变形法能将多向应变计组的应变值有效地转化为应力值。利用最大熵原理建立相应的模型，并在此基础上求得监控指标，该指标避免了人为假定分布，合理可行。采用遗传算法优化拉格朗日乘子简单迅速，是一种比较好的优化方法。

［1］ 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.

［2］ 郑东健，郭海庆，顾冲时，等.古田溪一级大坝水平位移监控指标的拟定［J］.水电能源科学， 2000， 18（1）:16-18.

［3］ 陈江，段会文.混凝土徐变应力计算方法及应用［J］.水力发电，2011， 37（1）:92-94.

［4］ 袁琼. 二滩拱坝应力监测分析［J］.水电站设计，2003，19（3）:37-40.

［5］ 陈建军，曹一波，段宝岩.结构信息熵与极大熵原理［J］.应用力学学报， 1998， 15（4）:116-121.

［6］ 丛培江，顾冲时，谷艳昌.大坝安全监控指标拟定的最大熵法［J］.武汉大学学报信息科学版， 2008， 33（11）:1126-1129.

［7］ 刘杰，王媛.改进的遗传算法及其在渗流参数反演中的应用［J］.岩土力学， 2003， 24（2）:237-241.