基于离散纵标法与蒙特卡罗方法的三维耦合程序开发
2012-04-26韩静茹陈义学石生春袁龙军陆道纲
韩静茹,陈义学,石生春,袁龙军,陆道纲
(1.华北电力大学核科学与工程学院,北京 102206;2.环境保护部核与辐射安全中心,北京100082)
辐射屏蔽系统设计是核装置工程设计的核心内容之一,其设计优劣直接影响工程造价及工作人员与周围环境的辐射安全。目前常用的辐射屏蔽计算方法分为两种:确定性方法(如SN)和蒙特卡罗方法(MC)。其中SN方法特别适合求解几何相对简单的“深穿透”问题,并可提供整个模型的分布解。然而,其在处理复杂几何模拟上存在限制,同时计算时间和所需存储单元随维度增加而增加。MC方法的优势在于能够精确描述复杂几何结构,且其计算量不受维度的影响。但由于其抽样本质,对于大型系统深穿透问题,难以在合理的时间内给出可靠的计算结果。MC分段计算方法[1]虽然在一定程度上提高了MC方法计算效率,但由于分段计算中MC统计误差的连续传递性,对于有效解决深穿透屏蔽计算问题仍存在困难。
对于先进核装置及其厂房、反应堆堆坑底部、船用堆舱等复杂屏蔽计算问题,由于其体积庞大,几何结构复杂,有大块屏蔽或复杂孔道等特点,单一的SN或MC方法无法提供可靠的计算结果。为了解决这类屏蔽问题,最有效的方法是开发一种SN方法与MC方法的耦合方法。国际上已经进行了这方面的研究,比如美国橡树岭实验室开发的 DOT3.5-DOMINOMORSE[2],美 国 加 利 福 尼 亚 大 学 开 发 的DORT-PROBGEN-MCNP[3]等。此 类 研 究 工作仅支持二维SN方法与MC方法的耦合,且SN计算只限于R-Z几何,这无疑难以满足现代核装置精确屏蔽设计的要求。近来日本东芝公司采用DOMINO耦合方法实现了三维离散纵标程序 TORT 和 MCNP 的耦合[4],其 中TORT计算只限于直角坐标系,在圆柱坐标系问题计算中存在限制。目前国际上还没用发布基于三维SN和MC耦合方法的通用程序,而国内尚没有发现三维SN-MC耦合屏蔽计算方法研究方面的文献资料。
本文开发了三维SN-MC耦合计算方法,充分发挥SN方法解决深穿透问题的优势和MC方法模拟复杂几何的长处,提高其屏蔽计算的精度及速度,用于解决大型复杂核设施屏蔽计算难题。本文介绍了新开发的三维耦合屏蔽计算方法、程序系统以及基于该方法的耦合程序系统例题测试。
1 SN-MC耦合方法
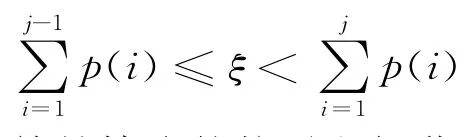
SN和MC方法是求解中子输运问题的两种不同方法。SN方法是在相空间(r×E×Ω)内对空间r、能量E和方向变量Ω采用直接离散方法数值求解中子输运方程,得到粒子角注量率ψ(ri,Eg,Ωm)。MC方法通过对大量单个粒子的运动历史逐个进行跟踪模拟,然后用统计方法作出随机变量某个特征的估计量,作为问题的解[5]。一般来说,SN-MC耦合屏蔽计算分析可以遵循下面的步骤:(1)模型划分:模型分解为适合SN计算的模型区及适合MC模拟的区域;(2)指定连接面:定义SN模型和MC模型的连接面;(3)SN计算:采用SN程序对SN模型区进行计算,得到连接面粒子角注量率;(4)转换计算:将SN计算得到的连接面粒子角注量率转换为粒子在空间、能量和方向上的概率分布;(5)MC源粒子抽样:编写MC自定义源抽样程序并嵌入MC程序,根据转换计算得到的概率分布进行源粒子抽样,依次确定源粒子的位置、能量和方向;(6)MC计算:采用MC程序,对上述源粒子进行跟踪模拟计算,得到所需计算结果。
SN-MC耦合方法关键是SN角注量率到MC源粒子参数概率转换的实现。三维SN-MC耦合方法采用如下方法实现上述转换:
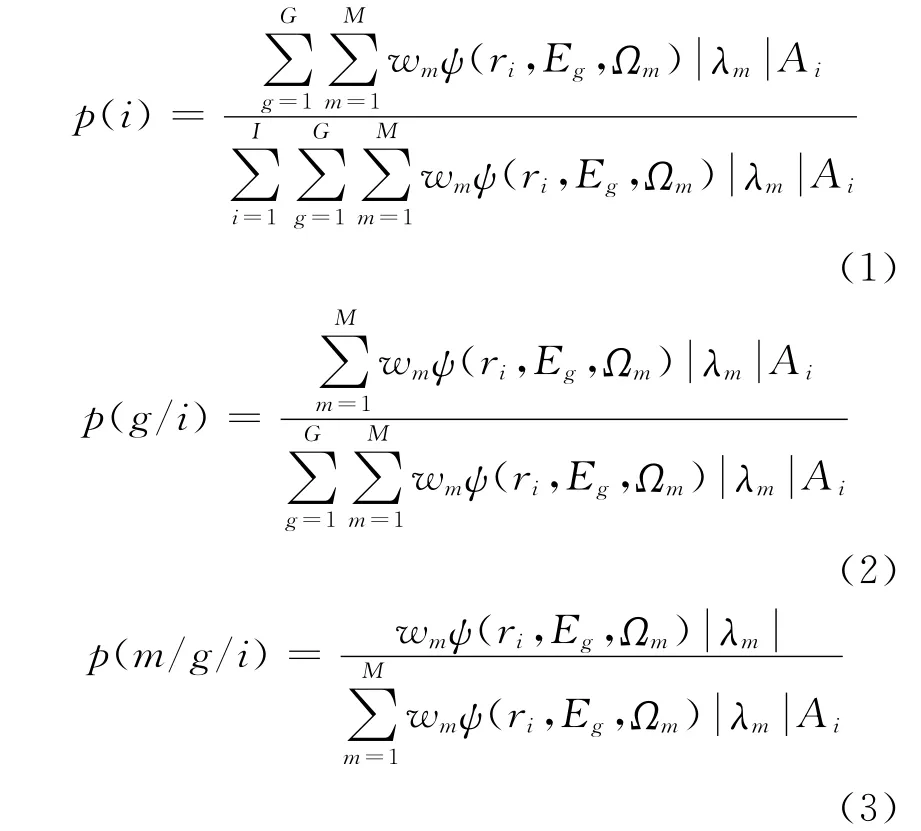
上式中,ψ(ri,Eg,Ωm)为网格ri、能群 Eg和离散方向Ωm区间内的粒子角注量率;wm为求积权重系数;λm表示粒子飞行方向与面法线方向的夹角余弦值;Ai表示网格区间ri对应的连接面面积;I为连接面网格数目;G为能群数目;M为离散方向数目。式(1)p(i)表示粒子落在网格区间ri内的概率;式(2)p(g/i)表示网格区间ri内,粒子落在能群Eg内的概率;式(3)p(m/g/i)表示网格区间ri内,能群Eg内,粒子落在离散方向Ωm区间的概率。
2 程序系统
三维SN-MC耦合程序通过编写接口程序,实现上述耦合方法。耦合程序系统流程图如图1所示。程序系统分为4个主要模块:SN计算模块、SN-MC接口程序、MC自定义源抽样程序和MC计算模块。
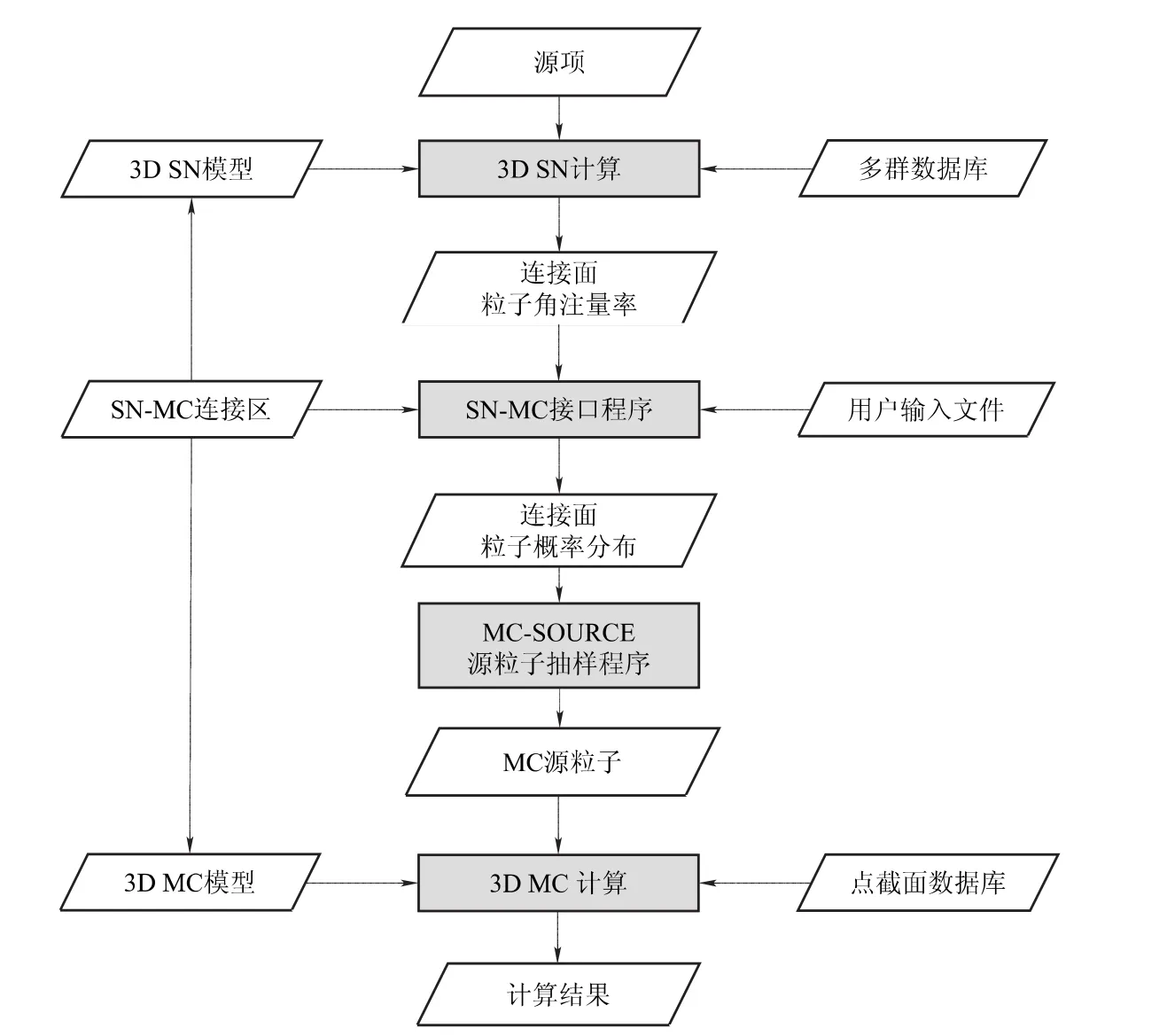
图1 三维SN-MC耦合计算示意图Fig.1 Sketch of 3D SN-MC coupled calculation
其中三维SN计算得到连接面的粒子角注量率,并以BNDRYS格式存储输出。SN-MC接口程序的主要功能是根据用户输入文件,将SN计算输出的角注量率文件转换为源粒子在空间、能群和方向区间上的概率分布。用户输入文件主要包括以下相关数据:SN模型坐标系、连接面网格划分,能群结构和求积组设置等。MC-SOURCE源粒子抽样程序,根据连接面的粒子概率分布进行MC源粒子参量抽样,获得粒子位置、能量和方向信息,为MC计算提供源项。利用MC-SOURCE抽取的源粒子信息进行MC计算,得到复杂几何区的粒子通量分布。该程序系统可以处理三维X-Y-Z及R-θ-Z 几何。
3 测试与分析
3.1 测试模型描述
采用三维 X-Y-Z 及R-θ-Z 几何例题对三维SN-MC耦合程序系统进行校核。其中SN计算采用TORT[6]程序及 MATXS10多群截面数据库。MC计算采用MCNP[7]程序及基于ENDF/B-Ⅵ评价核数据库开发的连续能量截面数据库[8]。不同于实际应用,测试例题选取了单独采用MCNP程序计算可以获得精确解的测试模型,以便与耦合计算结果进行对比分析。两个测试模型分别如图2和图3所示。

图2 测试模型1Fig.2 Test model 1
模型1是长×宽×高为20 cm×20 cm×24 cm的长方体。20 cm×20 cm×6 cm的中子源位于模型底部,在模型靠近上端水平面沿X方向依次设置20个探测器。模型2为半径26 cm,高40 cm的20°圆柱,源区为半径6 cm区域。0°和20°设为反射边界条件。其余为真空边界条件。测试模型的中子源均为各向同性的14 Me V中子,屏蔽材料为不锈钢和水的混合物(60a%SS316+40a%Water)。如图2和图3所示,连接面将模型分割为两部分:屏蔽区和探测器计数区。
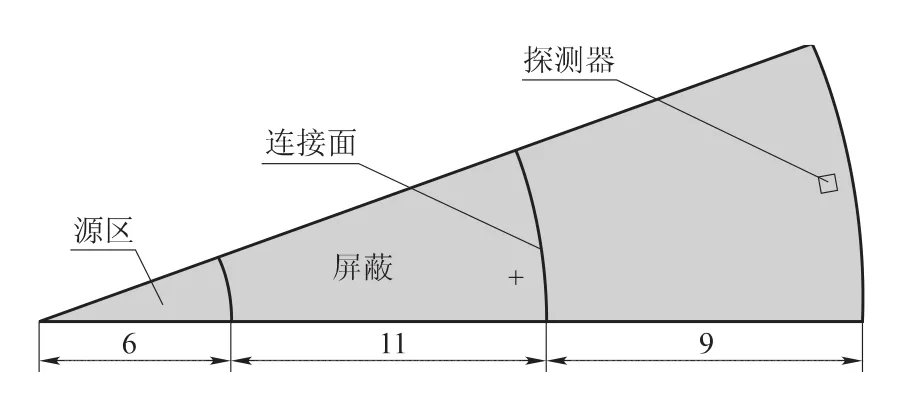
图3 测试模型2Fig.3 Test model 2
3.2 结果比较
耦合计算中,TORT计算建立整个模型,考虑周围材料对连接面源造成影响的同时,得到连接面角注量率分布和探测器处TORT计算结果。模型1和模型2分别采用直角坐标及圆柱坐标建立TORT模型,网格划分分别为:20×20×24和26×11×21个。TORT计算采用P3阶勒让德展开,S8全对称高斯求积组,离散方向个数为96。图4给出了模型1探测器处MCNP、TORT及TORT-MCNP三种程序计算的中子注量率结果对比。可以看出,基于这三种方法的计算结果吻合得很好。TORTMCNP耦合程序计算结果总体上介于TORT和 MCNP计算结果之间。TORT-MCNP与MCNP计算结果相比,中间探测器结果偏差在1%以内,两端探测器结果偏差稍大,在3%左右。这主要是由于SN和MC程序处理边界条件方式不同,对结果造成的影响。
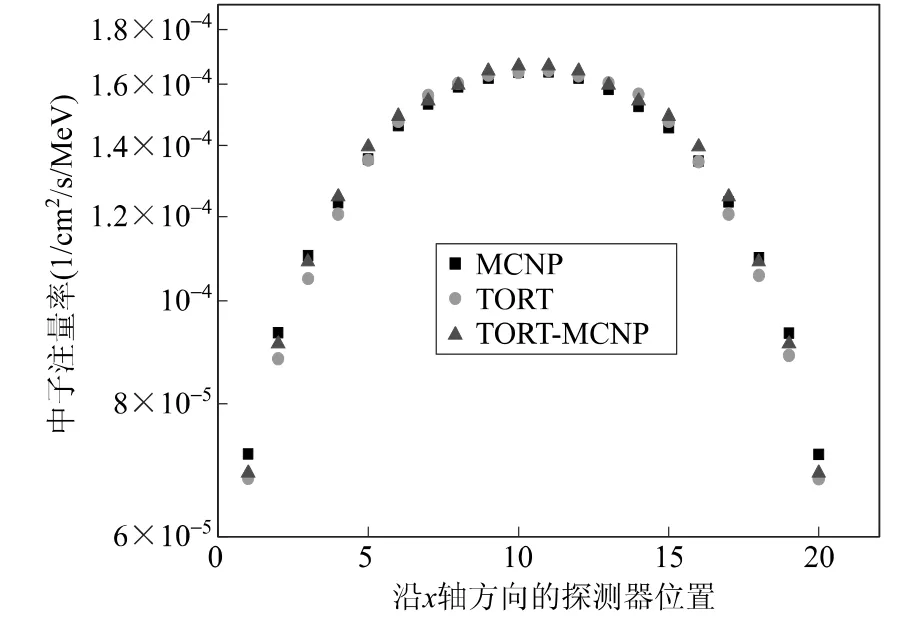
图4 模型1中子注量率比较Fig.4 Comparison of neutron flux of model 1
模型2因为角度方向采用反射边界条件,同一半径周向探测器计数结果相同,因此选取其中一个探测器进行计算。三种程序计算的探测器中子能谱如图5所示。TORT-MCNP耦合计算的探测器总中子注量率结果与MCNP结果相比相差小于1%。可以看出,基于这三种方法的计算结果吻合得很好,显示三维耦合程序可以提供屏蔽问题的精确解。

图5 模型2中子能谱比较Fig.5 Comparison of neutron spectrum of model 2
4 结论
基于SN和MC方法的耦合方法,开发了TORT-MCNP三维耦合程序系统。该程序集成SN方法解决深穿透问题的优点以及MC技术在复杂几何模型模拟方面的长处,克服常规屏蔽计算方法在大型核装置屏蔽分析方面的缺点,提高其屏蔽计算的精度及速度。通过X-YZ及R-θ-Z两种几何测试例题对耦合程序进行校核计算,并与MCNP及TORT结果进行比较。结果吻合良好,初步验证了三维SN-MC耦合方法及程序系统的正确性。下一步将对三维SN-MC程序系统进行进一步的基准验证并应用于实际工程。
[1] 钟兆鹏,施工,胡永明.用MCNP程序计算水平辐照孔道屏蔽 [J].清华大学学报(自然科学版),2011,41(12):16-18.
[2] Emmett MB,Burgart C E,Hoffman T J.DOMINO,a general purpose code for coupling discrete ordinates and Monte Carlo radiation transport calculations,ORNL-4853[R].USA:ORNL,1973.
[3] Eggleston J E,Abdou MA,Youssef MZ.The use of MCNP for neutronics calculations within large buildings of fusion facilities[J].Fusion Engineering and Design 1998,42:281-288.
[4] Masahiko Kurosawa,TORT/MCNP coupling method for the calculation of neutron flux around a core of BWR[J].Radiation Protection Dosimetry,2005,116(1-4):513-517.
[5] 谢仲生等.核反应堆物理数值计算[M].北京:原子能出版社,1997.
[6] RhoadesW A,Simpson D B.The TORT Three-dimensional Discrete Ordinates Neutron/Photon Trans port Code[R].ORNL/TM13221,Oak Ridge National Laboratory,1997.
[7] BRIESMEISTER J F.MCNP:A general Monte Carlo N-particle transport code,version 4C,LA-13709-M[R].USA:LANL,2000.
[8] WIENKE H,HERMAN M.FENDL/MG-2.0 and FENDL/MC-2.0,the processed cross-section libraries for neutronphoton transport calculations,version 1[R].Vienna,Austria:Nuclear Data Section,International Atomic Energy Agency,1998.
