快堆燃料组件六角形外套管截面变形的计算方法研究
2012-04-26王明政高付海杨孔雳
付 浩,王明政,文 静,高付海,李 楠,杨孔雳
(中国原子能科学研究院,北京102413)
快堆燃料组件外套管(图1)是反应堆堆芯中最重要的部件。在快堆堆芯环境中,多种因素会引起套管的变形:冷却剂压差引起套管截面变形;高温引起热膨胀,并可能发生蠕变变形;高中子通量造成材料辐照损伤,导致宏观力学性能退化,包括辐照脆性、辐照蠕变、辐照肿胀、辐照硬化、辐照疲劳等。通过堆芯组件外套管的变形计算,能够为堆芯结构、物理等方面的分析设计提供输入参数和安全评估依据[1-2]。目前,美国、法国、俄罗斯、日本、韩国等国家在研究组件变形方面的技术比较成熟,并开发出了 ABADAN、 NUBOW、 HARMONIE、ACME、ARKAS等计算程序。我国快堆技术起步较晚,目前还没有开发专门的堆芯组件外套管变形计算程序。

图1 快堆燃料组件结构示意图Fig.1 Structure of fuel assembly in fast reactor
本文分别对快堆堆芯组件六角形外套管在内外冷却剂压差的作用下的弹性变形,在温度场和中子场环境下的热膨胀、辐照蠕变和辐照肿胀等变形进行了理论分析,得到了计算快堆堆芯六角形外套管截面变形的方法。
1 弹性变形的分析计算
1.1 简化模型与变形计算
组件六角形套管截面可以认为是处在流体静压下的矩形平板,其边端固支。平板的挠度(图2)可用类似于弯曲梁挠度方程的微分方程来处理。在计算应力时假设在弯曲的情况下杆的横截面仍保持平面。在横向弯曲的情况下由于切应力小,仅根据法向应力就可以进行计算[3]。

图2 燃料组件六角形套管载荷计算图Fig.2 Calculation of the hexagonal duct of fuel assembly
平面弯曲轴的微分方程为以下形式

由此,得到了燃料组件外套管截面在冷却剂压力作用下的对边距计算方法,为后续单根组件变形和多根组件协调变形的研究工作提供了参考依据。为了证明方法的正确性,本文接下来对其进行了有限元计算,并将两种结果进行了对比。
1.2 截面的有限元数值分析
应用有限元计算软件ANSYS建立组件六角形套管截面(图3),对边距尺寸取59×10-3m,壁厚取1.2×10-3m,角点的倒角半径取为4.2×10-3m,采用四节点平面应力单元,材料模型选用线弹性,用四边形网格对结构进行划分。在角点处施加约束,防止刚体位移。假设在套管内壁上受到1×106N的均布压力。

图3 ANSYS建立的六角形套管截面Fig.3 Cross section of the hexagonal duct modeling by ANSYS
提取有限元结果上下两个壁面的中点位移历程,换算两点相对位移量即为套管截面“对边距”的变化量。
1.3 两种方法的计算结果对比
将同样的输入参数代入推导的Δs理论计算公式(3),同样可以计算出对边距变化量。图4给出了两者的比较结果。

图4 两种方法的结果对比Fig.4 Result comparison of the two methods
可以看出两组数值非常接近,计算结果相差很小。但是由于都是线性关系却不平行,差值有继续扩大的趋势。快堆燃料组件入口处冷却剂的内外压差是0.4~0.7 MPa,而在出口处小于0.1 MPa[3],也就是说组件外套管承受的压力不大于0.7 MPa。比较两种方法的计算结果,当压力为0.7 MPa时,理论计算和有限元计算的结果分别为1.224×10-4m和1.282×10-4m,误差仅为4.6%。即使压力达到1 MPa,理论公式计算和有限元算法得到的结果分别为1.748×10-4m和1.832×10-4m,相差8.4×10-6m,误差比例4.6%。这说明该理论公式在工程要求的精度范围内是可用的。
由此可见,理论公式(3)可以用于简单计算快堆燃料组件六角形套管的弹性变形,同时也证明了理论算法中建立的模型和做出的假设是合理的,分析方法和计算过程是可靠的。
2 蠕变和肿胀的分析计算
2.1 六角形截面的蠕变
在解蠕变问题时采用如下假设:(a)形变时截面保持平面;(b)在拉伸和压缩时材料的性能相同;(c)在辐照的情况下滑移理论的基本假设不变。
根据平面截面的假设,形变速率具有如下形式


可以用各种不同的近似法来解方程组(5)。解法之一是选择某个有Φ=Φ()R形式的蠕变速率势能的近似函数。在这个情况下,函数Φ是单位长度上的势能,这样当N=0时R=M,R是M和N的某种函数。
对于矩形截面

知道弯曲矩和曲率变化速率之间的关系,可用对方程积分的方法求得平面的挠度


应用所得到的关系式可以求得材料处于蠕变状态的套管壁面上任一点的“对边距”尺寸的变化和变形随时间的变化。在活性区对于快中子堆燃料组件工作条件来说,套管材料的韧性流动主要是由材料的辐照蠕变来决定。正如上面所指,一般来说,钢的辐照蠕变速率是应力的线性函数。因此对n=1的情况更有意义。
2.2 六角形截面的肿胀
堆芯环境下的套管截面在温度和辐照的作用下还会引起热膨胀应变εth和辐照肿胀εsw,分别用如下表达式计算这两种变形
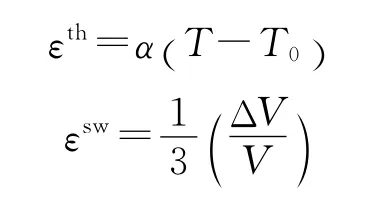

式中:α为热膨胀系数;T为计算温度;T0为参考温度;kt为辐照剂量。
由于热肿胀和辐照肿胀引起的套管的肿胀量的表达式为
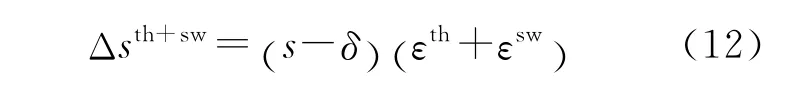
3 外套管截面的总变形
综上所述,堆芯组件六角形外套管的总变形可以用如下表达式来表示

将以下输入参数代入表达式,计算套管截面的总变形

假设温度起初为线性增长,在第200小时达到600℃,之后一直到第2 000小时一直保持在600℃。计算得到套管截面从时间1到2 000小时的总变形(图5)为0.63 mm。从变形量随时间的变化图和最大变形量来看,计算结果基本符合实际变化趋势,是合理可靠的。
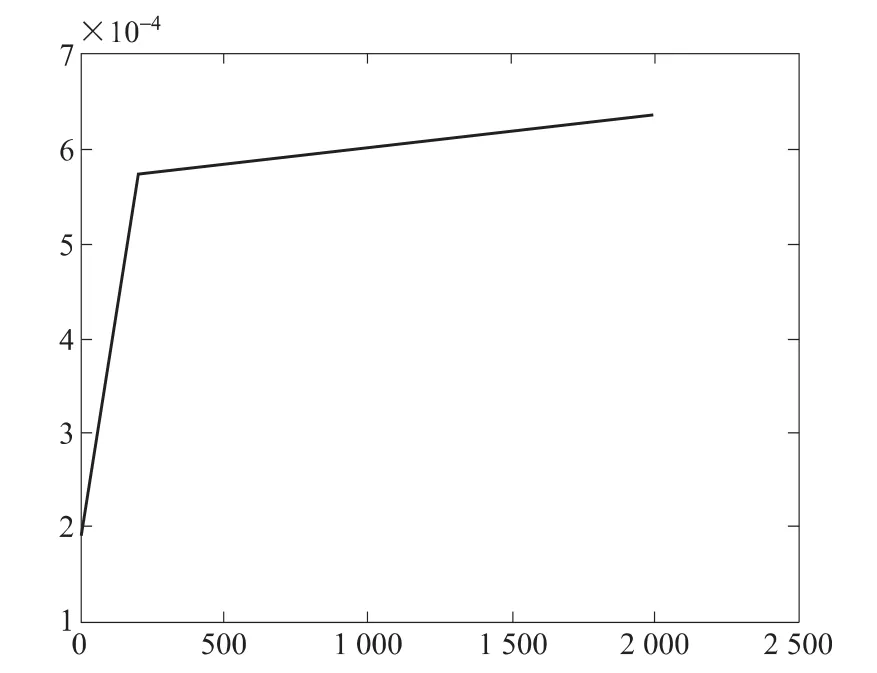
图5 套管截面总变形量随时间的变化图Fig.5 Cross section deformation of the hexagon duct versus time
4 结论
综上所述,快堆六角形外套管截面的总变形由弹性变形、热肿胀、辐照肿胀、蠕变几部分构成。本文在合理的假设前提下分别建立了简化模型,对快堆堆芯组件套管截面变形的计算方法进行了研究和探索。
[1] 苏著亭,叶长源,等.钠冷增殖堆[M].北京:原子能出版社,1991.
[2] 谢光善,张汝娴.快中子堆燃料元件[M].北京:化学工业出版社,2007.
[3] 查波得卡,等.快堆燃料组件运行性能,1994.
