贝叶斯网络用于屏蔽泵系统故障分析方法的研究
2012-04-26鲍依兰黄高峰佟立丽曹学武
鲍依兰,黄高峰,佟立丽,曹学武
(上海交通大学机械与动力工程学院,上海200240)
贝叶斯网络(Bayesian Network,BN)是基于概率论和图论的一种不确定性知识表达和推理网络,最早由Judea Pearl[1]于1988年提出,研究其在机器学习、数据挖掘及数据统计的应用,近年来,贝叶斯网络在人工智能领域得到不断发展和改进,使其成为不确定推理中最有力的工具,贝叶斯网络已成功应用于计算机智能科学、医疗诊断和工业控制等众多领域。目前,系统故障分析常用的方法是故障树模型分析方法,故障树分析法适用于故障机理、故障逻辑关系清晰的系统,需要对系统的故障树模型做简化假设:事件状态的二态性、基本底事件间相互独立和故障逻辑关系的确定性[2]。而事实上阀门存在正常、拒开和破裂等多故障状态,许多故障间的因果关系是不确定性的逻辑关系,以及在获得新的故障样本后希望对分析数据能够及时更新,对系统的故障进行及时准确分析等问题,因此,本文以屏蔽泵系统故障分析为实例,应用贝叶斯网络解决实际系统故障分析中的问题,最后由贝叶斯网络自身强大概率推理能力[3-4]对屏蔽泵系统故障状态进行及时有 效分析。
1 贝叶斯网络模型
贝叶斯网络[1]是一个有向无环图(Directed Acyclic Graph,DAG),由代表变量的节点及连接这些节点的有向弧构成,有向弧由父节点指向子节点,用单线箭头“→”表示。BN由网络拓扑结构和局部条件概率表(Conditional Probability Table,CPT)两部分构成,没有任何父节点的节点称为根节点,对应的条件概率称为先验概率。通过定义网络中所有节点、节点间的关联(用有向弧表示)和指定条件概率表,就能表达BN中所有节点的联合概率,并且可以在已知任意节点状态信息条件下,进行网络推理,计算其他任意节点的条件概率。
1.1 贝叶斯网络学习
为了获得贝叶斯网络,把通过机器学习的方法从数据中获得BN的方法称为BN学习[5,6],BN 学习可分解为两个阶段:一是,网络拓扑结构即有向无环图的学习,简称结构学习;二是,网络中每个变量的局部条件概率分布的学习,简称参数学习。本文贝叶斯网络结构是由故障树模型转化方法获得,该方法具有简单可行的优点[2~4],本文主要研究BN参数学习,视参数θ为一个随机变量,采用贝叶斯估计方法,利用先验知识和数据样本对参数进行估计,获得其后验概率分布,贝叶斯估计公式如式(1)所示:
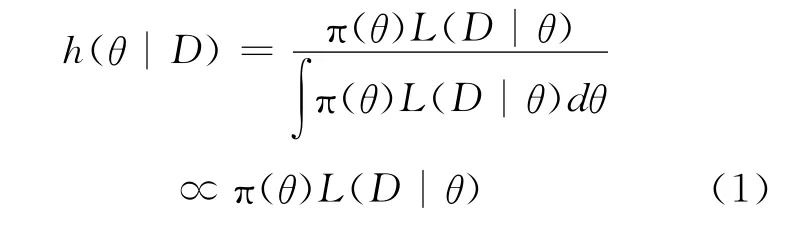
式中:L(D|θ)表示数据样本D的影响,称为似然函数,它是网络节点的状态变量样本观测值,可根据经验统计和记录确定节点状态的似然函数,对应π(θ)用于表示先验知识,称为先验概率分布函数,它是网络节点事件的发生概率,可根据历史资料或主观判断确定节点事件的先验概率分布。在贝叶斯方法中,合理的先验概率分布π(θ)确定是容易引起争议[5,7],另外核电厂设备故障分析数据匮乏和仅从一个特定电厂的运行经验结果不具有统计意义,本文采用共轭先验分布和设备故障的国际通用数据确定先验知识,主要针对设备故障分析数据中的两个重要参数:需求失效概率和运行失效率,通过贝叶斯网络学习来确定它们的后验分布参数估计。
1.2 共轭先验分布族
实际应用中根据公式(1)计算后验分布密度是比较复杂的,因此,Raiffa和Schaifeer提出共轭分布族。根据文献[7]的研究,需求失效概率(pi)和运行失效率(λ)的共轭先验分布可分别采用样本来自平稳独立二项式分布过程的Beta分布和样本来自平稳独立Poisson分布过程的 Gamma分布[7],因此,pi和λ的Bayes估计可分别由下面公式(3)和(5)来确定。
进行m次设备需求失效试验或运行失效试验,在第i(i=1,2,…,m)次试验中,试验时间为ti(t1<t2<…<tm),对应的试验设备样本数为ni,若试验结果有ri(ri=0,1,…,ni)个失效(对应设备需求失效次数或设备运行失效次数),记(ti,ni,ri),i=1,2,…,m 为本次试验获得的数据。
1.2.1 设备需求失效概率的Bayes估计
在需求失效试验中,假设失效次数ri是一个二项分布过程,根据pi的共轭先验分布和公式(1),设备需求失效概率pi的后验分布函数如公式(2)所示:
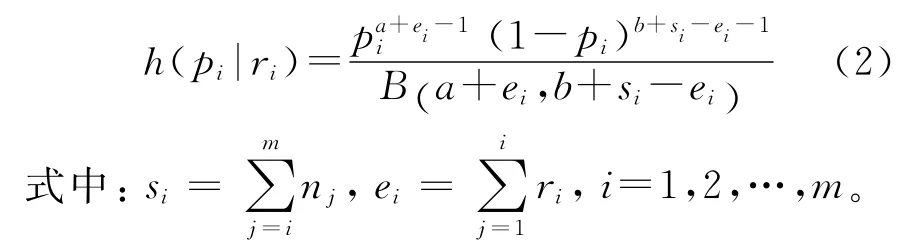
用pi后验函数的数学期望,作为设备需求失效概率pi的Bayes估计,后验需求失效概率pi是先验参数和样本失效次数的函数,如公式(3)所示:
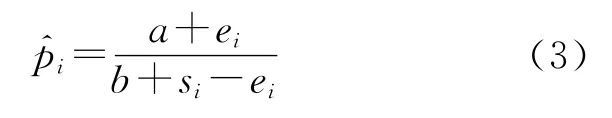
1.2.2 设备运行失效率的Bayes估计
在设备运行失效试验中,假设失效次数ri是泊松分布,根据λ的共轭先验分布和公式(1),设备运行失效率λ的后验分布函数如公式(4)所示:

若运行失效概率服从指数分布,则在给定任务时间t内的运行失效概率由公式(6)计算:

1.3 贝叶斯网络推理
贝叶斯网络是建立在节点变量的概率约束上,表达了节点变量间的条件独立性,基于网络结构(定性)和参数(定量)知识可以进行不确定性双向推理计算[8]。贝叶斯网络正向推理获得网络中节点的联合概率和任意节点发生概率,其数学描述为:论域中U={x1,x2,…,xn}对应于网络中的节点,pparents(xi)表示xi父节点的集合,联合概率p(x1,x2,…,xn)如公式(7)所示:

贝叶斯网络反向推理获得在已知某些节点信息条件时的其他节点的条件概率,例如,随机变量xi具有 m 个事件状态{xi1},{xi2},…,{xim},假设已知其他节点的信息为V,则在该已知条件下xi处于各事件状态的发生概率由公式(8)计算:
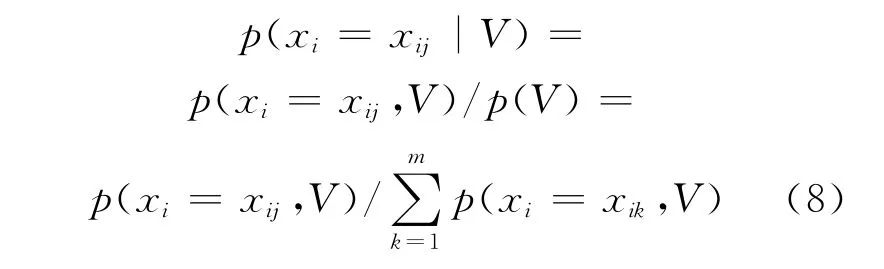
2 基于贝叶斯网络的屏蔽泵故障分析
故障树分析方法(Fault Tree Analysis,FTA)是一种将系统故障形成的原因由总体至部分按树枝状细化的分析方法,是系统概率安全分析和故障分析的一种重要方法。本文基于故障树模型中各相关事件间的因果关系构建屏蔽泵故障的贝叶斯网络拓扑结构,故障树模型转换获得贝叶斯网络得到研究[2,3]。
2.1 屏蔽泵故障的贝叶斯网络拓扑结构
本文建立的屏蔽泵故障贝叶斯网络结构如图1所示,论域中共有43节点事件,第43节点为屏蔽泵故障事件T,网络中其他节点事件定义和编码见表1。
2.2 基于BNT的屏蔽泵故障贝叶斯网络参数学习

图1 屏蔽泵故障的贝叶斯网络Fig.1 Fielded pump failure Bayesian network
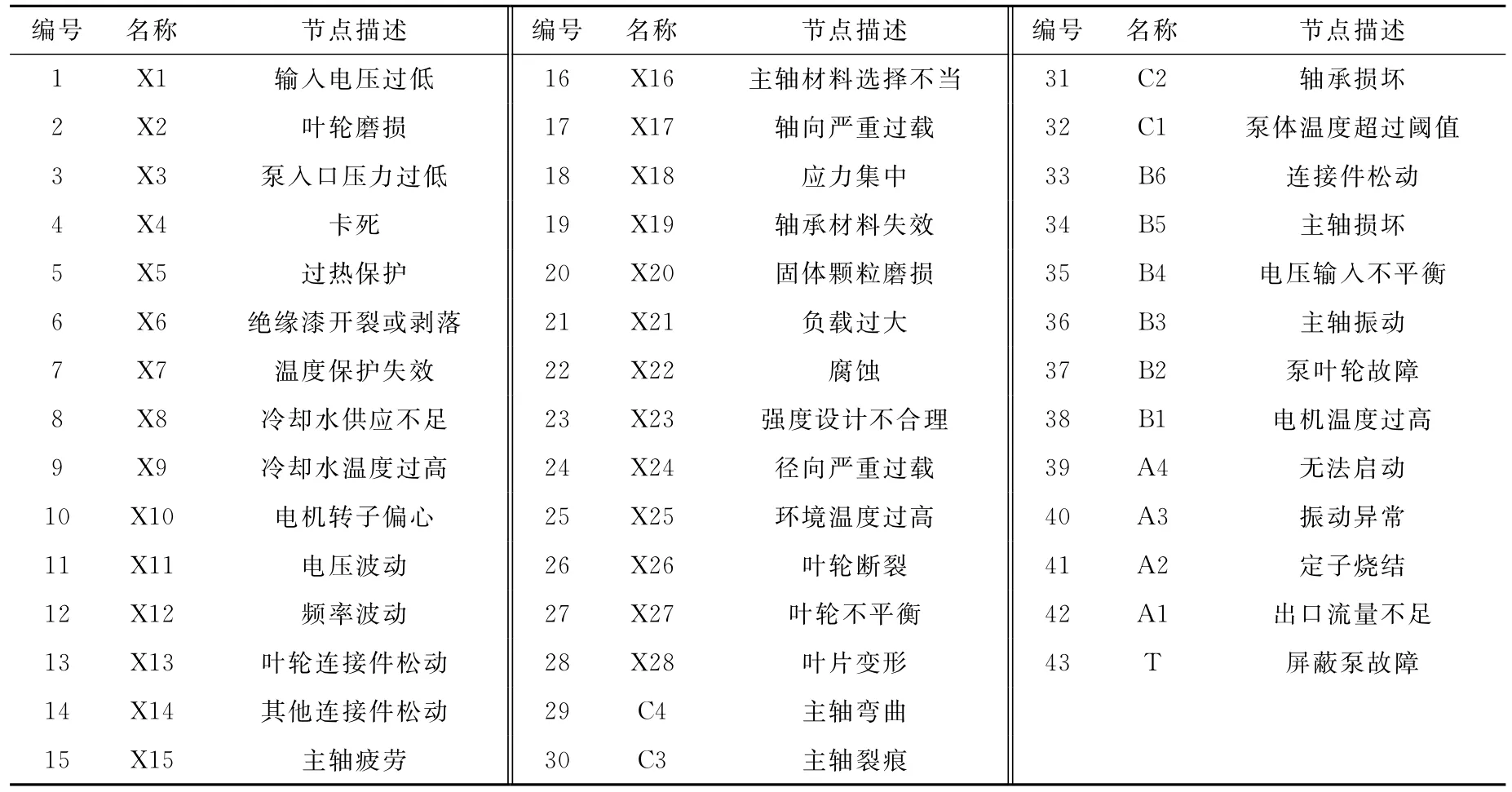
表1 模型中各节点事件定义Table 1 Definition of each nodes event in model
采用MATLAB语言编制的贝叶斯网络工具箱(Bayesian Networks Toolbox,BNT),进行屏蔽泵故障贝叶斯网络参数学习和推理,此工具箱在贝叶斯学习编程方面非常灵活。但BNT中仅提供了Beta先验分布的参数学习机制,可以获得设备需求失效概率的估计,而为了计算运行失效率参数,本文基于上一节贝叶斯网络学习理论,在BNT软件中新增先验分布为Gamma分布的失效率参数学习机制。屏蔽泵故障贝叶斯网络中初始先验参数假定,令根节点X2和X3为设备失效率事件,失效率先验参数基于Jeffreys的无信息Gamma先验分布;其他节点事件是设备需求失效事件,失效概率先验参数基于Jeffreys无信息Beta(0.5,0.5)先验分布[7]。另外节点状态变量说明,贝叶斯网络具有多状态表达能力,本文例举研究,当根节点X22为三状态时候,对应事件描述为:腐蚀严重、无腐蚀和一般腐蚀,节点状态值分别为“1、2和3”,其他网络节点为二态,状态取值为:“1”表示节点事件故障状态,“2”表示节点事件正常状态。为了描述方便,将该初始网络称为bnet1网络。
在屏蔽泵系统设备故障统计中,能够收集到相关设备失效概率的通用数据,在网络bnet1先验参数基础上,本文用BNT软件中参数学习机制,获得各根节点的通用数据,进一步讨论获得新样本后的进行网络参数学习,表明了贝叶斯网络不仅具有学习功能,还能在新信息条件下不断更新,获得设备新样本下故障分析。因此,本文进行了二次网络参数学习,第一次参数学习获得根节点通用数据的网络称为bnet2,第二次在新样本数据下的参数更新学习,获得的网络称为bnet3。
图2是三个网络(bnet1、bnet2和bnet3)所有节点的部分参数比较,发现:一、bnet2网络中各根节点的参数为相应通用数据;二、bnet3在获得新样本后,得到进一步网络参数更新,由图22中bnet2和bnet3曲线可见,节点X3和A1的参数变化较大。分析变化原因:节点X3参数是由公式(6)计算得到,失效率参数在学习中与新样本中运行失效次数有关和试验运行时间有关,两者使得节点X3参数的变化;另外,节点A1参数是失效概率参数学习,它仅与新样本中出现的需求失效次数有关,当新样本中出现节点A1失效事件,由公式(3)计算出新样本下的参数。三、对比bnet1先验参数,bnet2和bnet3网络参数学习后,可获得中间节点的逻辑关系。如故障树模型中B1和B3节点与上层节点的分别是“逻辑与”和“逻辑或”关系,图3和图4分别是它们在三个网络中的CPT,由图可见,经过学习的网络参数可表达,“逻辑与”:当父节点事件全部发生时,B1节点发生事件对应的CPT值大于0.9,否则B1节点发生事件对应的CPT值小于0.1;“逻辑或”:只要有一父节点发生,B3节点发生事件对应的CPT值大于0.9,否则B3节点发生事件对应的CPT值小于0.1。四、BN可以表达多状态事件,图5是网络中三状态节点X22对应的参数值,可以看出先验分布的bnet1网络参数经过样本学习后,获得节点事件各状态时的发生概率,贝叶斯网络表达多状态事件比故障树模型简单方便。

图2 bnet1、bnet2和bnet3贝叶斯网络参数学习比较Fig.2 Network parameters comparison of bnet1,bnet2 and bnet3 network

图3 三个贝叶斯网络中“逻辑与”节点B1的参数CPTFig.3 Parameters comparison of“logic and”B3 node in three Bayesian networks

图4 三个贝叶斯网络中“逻辑或”节点B3的参数CPTFig.4 Parameters comparison of“OR logic”T node in three Bayesian networks
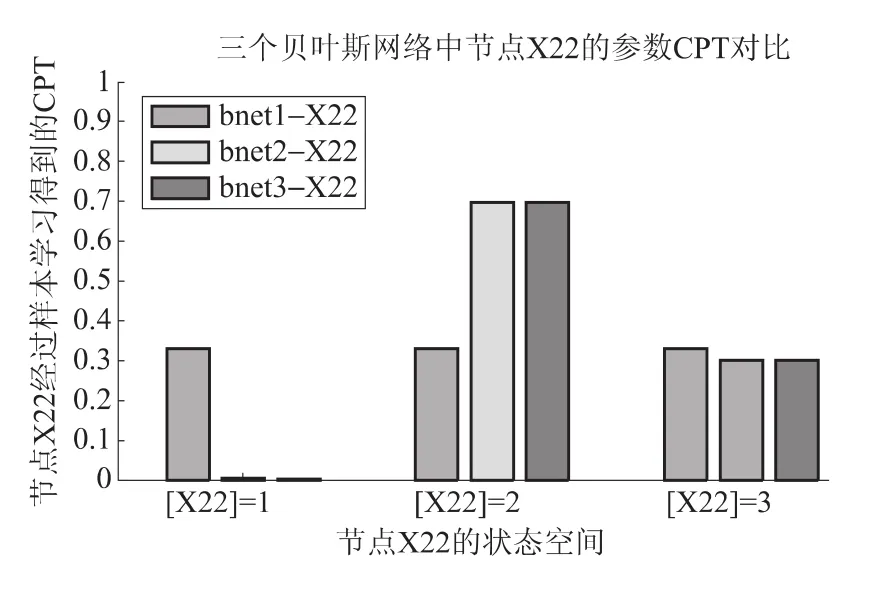
图5 三个贝叶斯网络中多态节点X22的参数CPT值Fig.5 Parameters CPT comparison of multi-fault state node in three Bayesian networks
2.3 屏蔽泵故障贝叶斯网络的推理
贝叶斯网络具有双向推理功能,定量地给出各元件在系统可靠性中所占的地位,本文通过贝叶斯网络推理分析屏蔽泵系统故障的薄弱环节所在、出现最可能的故障模式及其发生概率。
2.3.1 未知证据的贝叶斯网络推理
首先计算在没有证据时各节点全概率,它体现了在证据未知情况下,对各种节点事件的一种置信度(表2),是屏蔽泵故障节点T及其父节点的发生概率。

表2 未知证据时屏蔽泵故障及其父节点事件的概率值Table 2 The failure probability of fielded pump and parent node event in no-evidence case
表2中横项是三个学习网络的推理结果,列项是屏蔽泵故障与各节点的发生概率,可看出无证据时屏蔽泵故障的概率为0.9411,而且对其贡献最大的是振动异常,其次是出口流量不足,而定子烧结对其影响很小。另外,发现网络bnet3的屏蔽泵故障概率比bnet2高,因此,获得新样本后对网络参数进行更新是很有必要。
2.3.2 已知简单证据的贝叶斯网络推理
若现在调研获知叶轮破损,对应根节点X2发生状态为“1”时,此时可以由网络正向推理进一步获得,在该证据时屏蔽泵系统故障和其他节点的故障信息,如表3所示。
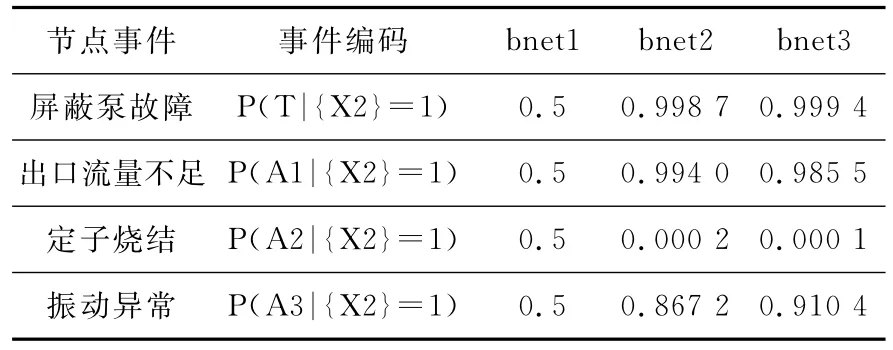
表3 已知evidence{X2}=1证据时屏蔽泵故障及其父节点事件的概率值Table 3 The failure probability of fielded pump and parent node event in evidence{X2}=1 case
从表3发现,经过参数学习后的网络bnet2和bnet3,在已知叶轮破损后,“出口流量不足”事件的发生概率大大提高,并预测到此时屏蔽泵故障发生概率比无证据时大。总结,通过贝叶斯网络可以得到在给定任意节点证据时,各层节点事件的发生概率,找出对屏蔽泵故障影响最大的事件,在实际工作中首先对这些事件进行维修。
2.3.3 屏蔽泵系统故障分析
上述主要比较了通过参数学习获得的三个网络,为了剖析屏蔽泵系统故障,下面对网络bnet2在已知屏蔽泵故障证据(节点T发生)时进行后向推理,分析屏蔽泵系统的故障原因,找到系统的薄弱环节。
(1)如下各根节点对屏蔽泵故障影响排序(号码为各节点的编号),可得屏蔽泵故障主要受节点X3的影响,对应事件是“泵入口压力过低”事件,其次是节点X11和节点X1,对应“电压波动”和“输入电压过低”事件的影响也较大。
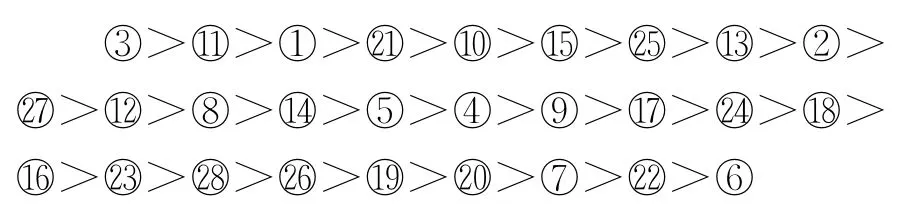
(2)已知evidence{T}=1证据,计算联合节点[X1,X2]和[X22,C2]的概率分布,分别如图6和图7所示。由图6得出,屏蔽泵故障由于节点X1和X2同时故障导致可能性很小;由图6得出,节点X22增加“事件状态3”,该状态对屏蔽泵故障的概率贡献见图7第三个分布,可见是不容忽略的状态。

图6 bnet2网络在evidence{T}=[1]证据时[X1 X2]的联合概率分布Fig.6 The joint probability[X1 X2]of bnet2 in evidence{T}=[1]case

图7 bnet2网络在evidence{T}=[1]证据时[X22 C2]的联合概率分布Fig.7 The joint probability[X22 C2]of bnet2 in evidence{T}=[1]case
(3)表4是bnet2网络在屏蔽泵系统故障时的推理分析,屏蔽泵系统中最大可能的故障模式是:泵入口压力过低、振动异常和出口流量不足导致屏蔽泵故障。

表4 网络bnet2对屏蔽泵系统故障的推理分析Table 4 The inference analysis to fielded pump failure in bnet2 network
3 结论
与故障树分析方法比较,贝叶斯网络具有表达多故障状态和不确定性逻辑关系的能力,本文建立含有多状态节点的屏蔽泵故障贝叶斯网络模型,并在贝叶斯网络工具箱软件中,新增设备故障运行失效率参数的学习机制,通过对网络中参数的学习,获得根节点发生概率为通用数据的网络和进行新样本学习后的网络,最后由网络推理剖析屏蔽泵系统故障原因,屏蔽系统故障分析的结论为:泵入口压力过低、电压波动和输入电压过低是屏蔽泵系统的薄弱环节,振动异常和出口流量不足是屏蔽泵故障的直接原因。综上,贝叶斯网络能够用简洁直观的图形描述系统中各单元部件间复杂的因果关系和多状态故障事件,并在网络节点有新样本信息时,贝叶斯网络的学习机制可更新网络参数,结合先验知识和样本信息,由贝叶斯网络强大的不确定性推理能力,给出详细的概率解释,因此,贝叶斯网络能够作为故障分析方法,为研究系统故障模式和机理提供有效途径。
[1] Pearl J.Probabilistic Reasoning in Intelligent Systems:Networks of Plausible Inference [M].Revised second Printing,Morgan Kaufmann Publishers,Inc 1988.
[2] 王广彦,马志军,胡起伟.基于贝叶斯网络的故障树分析[J].系统工程理论与实践,2004,24(6):78-83.
[3] 周忠宝,董豆豆,周经伦.贝叶斯网络在可靠性分析中应用 [J].系统工程理论与实践,2006,(6):95-100.
[4] Bobbio A,Portinale L,Minichino M,et al.Improving the analysis of dependable systems by mapping fault trees into Bayesian networks[J].Reliability Engineering System Safety,2001,71(3):249-260.
[5] 林士敏,王双成,卢玉昌.贝叶斯方法的学习机制与问题求解 [N].清华大学学报,2000,40(9):61-64.
[6] Cooper Gregory F,Edward Herskovits.A Bayesian Method for the Induction of Probabilistic Networks from Data[J].Machine Learning,1992,l9(4):309-347.
[7] 马静娴,严国奎,刘志军.用贝叶斯方法处理核电站PSA分析中的设备可靠性数据[A].2004年全国机械可靠性学术交流会论文集[C],2004.
[8] 徐宾刚,屈梁生,陶肖明.转子故障贝叶斯诊断网络的研究[J].机械工程学报,2004,40(1):66-72.
