一类点权网络的最小费用流问题*
2012-04-12高明霞贺国光
高明霞 贺国光
(兰州交通大学交通运输学院1) 兰州 730070) (天津大学管理学院2) 天津 300072)
典型的最小费用流问题是指在一个给定的网络中求一个从发点到收点的流值为某一给定常数的流,使其费用最小[1].在这个网络中,流量除了满足节点的守恒条件之外,其调整和增加只受边上容量的限制,对应费用也是由各边费用得到,称这类网络为弧权网络,平常所说的网络皆是指这类弧权网络.对弧权网络中最小费用流问题的求解已经有负回路算法、最小费用路算法和原始对偶算法等有效算法[2].
但有些情况下,网络流量不但受边上容量的限制,还取决于其所流经的节点的容量,称这类网络为点权网络[3],城市道路网就是一类典型的点权网络.如果在城市道路网中进行目标为费用最小的物资输送或车辆调派,除路段通行能力之外,交叉口尤其是信号交叉口的通行能力也是限制物资或车辆流量的重要因素,交叉口处产生的费用也不能忽略.以往考虑节点容量的最小费用流算法如最小点截割法[3]、连续时间网络的最小费用流算法[4-5]等考虑的都是节点的总容量,即一个节点只有一个容量权重.而城市道路网中由于信号配时等原因,即使是同一个交叉口,在不同走向(如左转、直行、右转)的通行能力并不相同,经过交叉口j去往下一个交叉口k的车辆,在j处的延误和通行能力限制如何,取决于该车是如何到达j的,上述算法不具有这样的方向性.
本文将交叉口不同方向的延误和通行能力作为节点权重,建立了包括节点分方向权重和弧权的点权网络来表示城市道路网,并对普通网络最小费用流问题的最小费用路算法做了改进,给出了一个时间复杂性为O(nmf0)的最小费用路算法.其中:n,m,f0分别为网络中节点个数,边的条数和给定起点的流值.求解这类点权网络中的最小费用流问题,其中费用为时间.
1 算 法
1.1 相关符号和变量
用网络中的节点代表交叉口和特定起终点,用弧代表相邻交叉口之间的路段,将城市道路网表示为有向网络G=(V,A,D,C,T,U).式中:V={vi,i=1,2,…,n}为顶点集合,|V|=n;D={dijk,i,j,k=1,2,…,n}为点权集合,表示由节点i经j至k时在j处产生的延误;C={cijk,i,j,k=1,2,…,n}为点权集合,表示由节点i经j至k时在j处的通行能力;A={(i,j),i,j=1,2…,n}为弧集合,|A|=m;T={tij,i,j=1,2,…,n}为弧权集合,表示路段(i,j)的走行时间;U={uij,i,j=1,2,…,n}为弧权集合,表示路段(i,j)的通行能力;节点1和n分别为起点和终点.
除上面的符号之外,定义以下符号和变量:fij为流经路段(i,j)的流量;fijk为流经节点j的流中来自i欲去往k的流量;f0为源点给定的待输送流量;f,f*为网络当前的流及其流量大小;P为流的增广路或最小费用路;p[i]为增广路或最小费用路中节点i的前一个节点.
1.2 算法步骤
算法步骤如下.
步骤0 给网络一个初始可行流f(如零流).
步骤1 构造与当前流对应的残量网络

步骤2 在残量网络中寻找源点至终点走行时间最短的路径P,若不存在这样的路线,则计算结束,网络中不存在流值为f0的可行流,否则转步骤3.
步骤3 沿路径P增广θ个单位的流量,其中θ=min(θ1,θ2,f0-f*),θ1=min(uij-fij,cijk-fijk),if(i,j)∈P+and (j,k)∈P+,θ2=min(fjk,fkji);if(i,j)∈P-and(j,k)∈P-.式中:P+,P-分别代表路径P上前向弧和后向弧的集合.


其中步骤2中最短路径的求解采用标号修正算法逐步逼近最优解,定义为第k次检查标号时起点1至节点i的最短走行时间,算法步骤如下:
1.3 算法时间复杂性分析
由以上步骤可知,算法的主要工作量在于连续地寻找最小费用路并增广,由于每次增广使得流值至少增加一个单位,所以步骤1~步骤3最多循环f0次,所以整个算法的复杂性等于O(f0)乘以最短路算法的复杂性.步骤2中最短路算法的主要工作量在于步骤2.2中方程的循环迭代,在第k次循环中,计算每个只需检查节点j的所有入弧,故步骤2.2的工作量为O(m),总共最多循环n-1次,所以最短路算法的复杂性为O(nm);因此整个算法的复杂性为O(nmf0).
2 算 例
在图1所示的道路网中,节点1代表起点,节点14代表终点,其他节点代表城市道路网中的交叉口,假设所有交叉口皆为信号交叉口,所有路段皆为双向通行.假设起点1处有一定数量的车流要派往终点14,要求车辆总走行时间最短,派送方案可以通过求解1至14的最小费用流确定.为简便起见,算法中只考虑与节点1至节点14流量方向一致的走向,为避免残量网络中出现重复边,对2个走向都与流量走行一致的路段,加入虚拟节点(图2中15~20)代表该路段的中点,即路段两端至虚拟节点的走行时间皆为路段走行时间的一半,则图1表示的道路网络图简化为图2所示的有向网络.节点分方向权重见表1,网络中各弧权重见表2.
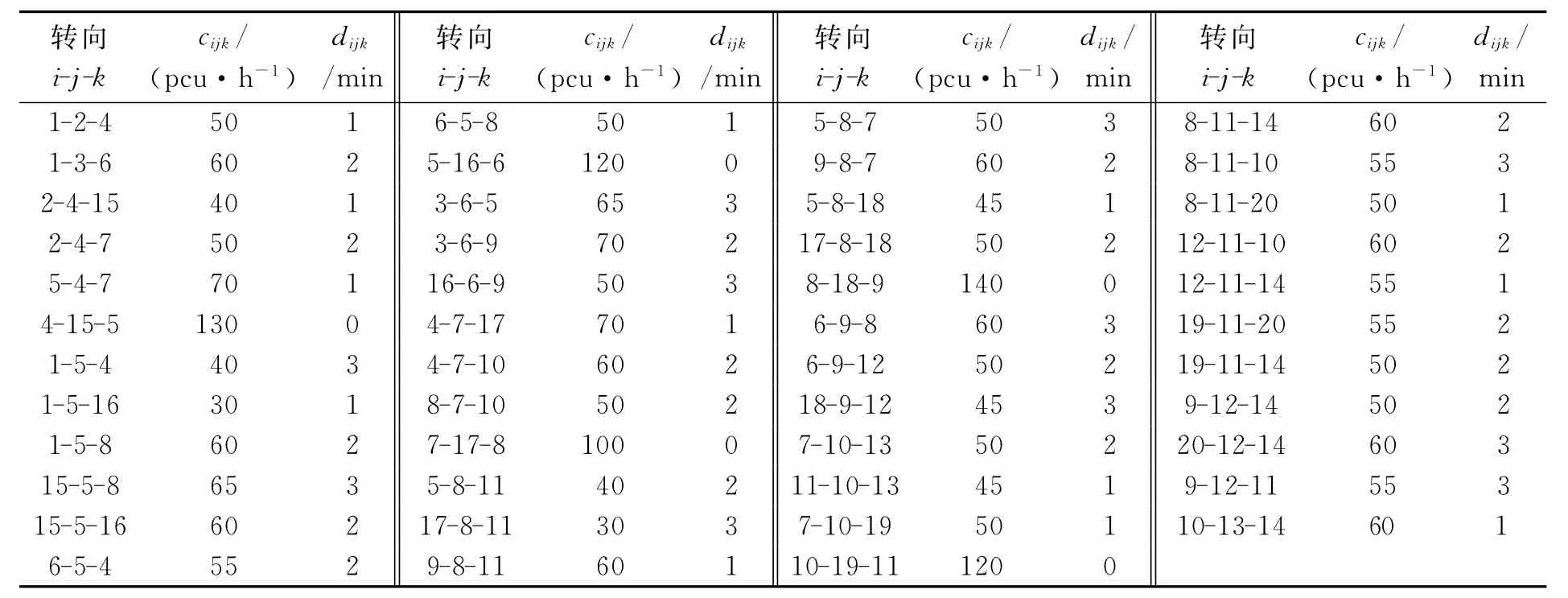
表1 交叉口分方向通行能力与延误(以cijk和dijk表示)
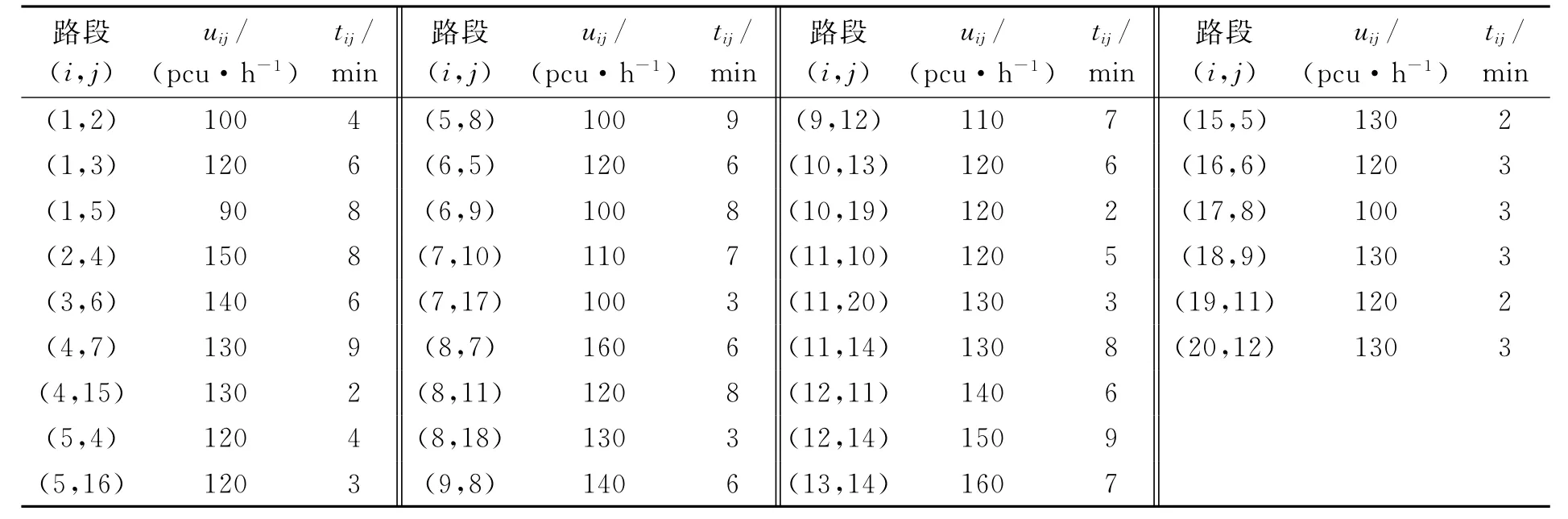
表2 路段通行能力uij和走行时间tij
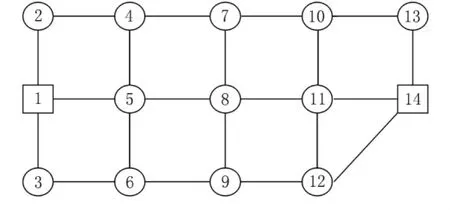
图1 算例的道路网络图

图2 由图1简化的有向网络
假定节点1处待调派的车流量为150pcu/h,运用上述算法求解起终点间的最小费用流,得到派送路线及相应流量和走行时间如表3所列.
3 结 论
如果在城市道路网中进行车辆调派或物资输送,交叉口的通行能力是限制流量的重要因素,交叉口延误占车辆整体走行时间的比重也很大,而且这两项因素具有很强的方向性,以往的最小费用流算法不具有这样的方向性.本文将交叉口不同方向的通行能力和延误作为节点权重建立点权网络,并给出了一个在这类点权网络中求解最小费用流的最小费用路算法,算法复杂性为O(nmf0).其中:f0是参数,通常认为f0可取到最大流流值,所以该算法不是多项式算法.不过在此基础上通过一定的变尺度技术,可以得到该类问题的多项式算法,具体的变尺度方法可参考文献[6].其中交叉口延误可以利用流量数据根据Webster公式等计算[7],交叉口不同方向的通行能力可以根据饱和流率等模型计算[8].

表3 车辆调派路线及相应的走行时间和流量
[1]谢金星,刑文训.网络优化[M].北京:清华大学出版社,2000.
[2]谢 政.网络算法与复杂性理论[M].长沙:国防科技大学出版社,2003.
[3]吴文泷.图论基础及应用[M].北京:中国铁道出版社,1994.
[4]Anderson E J,Nash P,Philpott A B.A class of continuous network flow problems[J].Math.Oper.Res.,1982,7:501-514.
[5]董振宁,孔淑兰.连续时间网络上的最小费用流问题[J].山东大学学报:理学版,2003,38(2):50-54.
[6]Ahuja R K,Magnanti T L,Orlin J B.Network flows:theory,algorithms,and applications[M].Eng1ewood Cliffs,New Jersey:Prentice Hall,1993.
[7]王殿海.交通流理论[M].北京:人民交通出版社,2002.
[8]任福田.道路通行能力手册[M].北京:中国建筑工业出版社,1991.
