高速公路作业区宏观动力学交通流模拟
2012-04-12张翛
张 翛
(山西省交通科学研究院黄土地区公路建设与养护技术交通行业重点实验室 太原 030006)
随着我国高速公路的发展,养护维修工作日益繁重,将会有越来越多的养护维修作业区在高速公路上出现.而道路养护维修作业区的交通管理水平,将直接关系到施工人员和道路使用者的安全、交通效率的高低等问题[1].
正确合理分析高速公路作业区交通流的动态特性就成为作业区交通管理、控制和诱导中的一项基本研究工作.文献[2]探讨了运动学波理论在高速公路作业区交通流分析中的应用.但是,运动学波只能用来分析稳态交通流下的激波的形成机理和传播速度,无法解释交通流的随时间变化的动态行为.本文在建立高速公路作业汇合区交通流的宏观动力学模型的基础上数值模拟了高速公路作业区汇合交通流的动态变化行为.
1 交通流的宏观动力学模型研究进展
由于高速公路交通流具有流动、波动、激波、压缩和扩散等流体性质,经典的宏观交通流模型将车辆看作流体;研究由大量车辆组成的车流集体的综合平均行为,用平均速度u(x,t)、平均密度ρ(x,t)及速度方差θ(x,t)等宏观量满足的方程来描述交通流,其单个车辆的个体行为并不以显式出现.宏观交通流模型主要包括流体力学模型(包括运动学模型和动力学模型)和以气体动力论为基础的动力论模型.
交通流动力学模型包含2个方程:连续性方程反映了车辆数的守恒定律,与LWR理论完全相同;运动方程描述车辆相互作用导致速度变化的动态过程,从而代替LWR模型中的平衡速度-密度关系.文献[2-3]描述了LWR模型,动态宏观连续交通流模型包括Pipes模型[4]、Payne模型[5]、Papageorgiou 模型[6]、薛郁模型[7]和Jiang模型[8].其中Jiang速度梯度模型是各项异性模型的代表,模型可以描述“时走时停”交通现象以及局部堆集效应,其模型控制方程为

式中:c0=Δ/τ≥0,为运动车流小扰动向后的传播速度;τ为扰动向后传播Δ距离所需的时间;T为弛豫时间.
2 作业区汇合交通的面积可变效应
汇合交通通常由2股或2股以上车流汇合而形成,通常情况下,汇合后的车道数小于汇合前的车道数之和,所以汇合处车辆容易减速而形成交通瓶颈.从宏观交通流的角度来看,车辆的这种汇合特性可以看作时车流对前方车道面积缩小做出的反映.从面积可变的角度,阻塞可模拟为流体管道中净流面积的减小.
具体地说,面积可变性对车流的影响与下列因素有关.
1)与车道面积减小的程度有关 定义面积可变系数为

式中:A为上游单元的车道面积(路面宽度);Aahead为其前一单元(下游)的车道面积(路面宽度).上述定义表明面积可变项只对面积(宽度)收缩路段起作用.
2)与车流密度有关 一般地,假设如下交通流状态,其中ρ和v分别为车流密度和速度;A为车道数;C为单车道通行能力.

对于多车道,当车流密度大于单车道密度时,车辆发生合流,要考虑面积改变的效应.且密度越大,对速度的削弱程度越大,阻塞越有可能发生.而当密度很小,接近单车道密度时,面积减小对车流影响不大,不必加入该项.
3)与车流速度的平方成正比 车流速度越大,阻塞越可能发生.这是一种经验规律,也是对面积可变项作量纲分析的结果.
4)与前方车道面积(宽度)有关 同样就面积收缩路段而言,前方车道面积小于考察单元时,引起了车流减速,前方剩余的车道面积越大,由面积收缩造成的减速影响就越小,反之,造成的减速影响越严重.设为A0标准退路宽度,为能通过一辆车的最小道路宽度(<A0),为能并列通过n辆车的最小道路宽度(<nA0),若不考虑自行车流干扰,计算时当<Aahead<,取Aahead=A0;当<Aahead<,取Aahead=2A0,依次类推.
这样在面积可变效应中,既考虑了前方车道面积的影响又保持了面积可变项为加速度量纲.
综上所述,面积变化等效力项可写为
3 高速公路作业区宏观动力学交通流模型
3.1 数学建模
考虑到汇合交通流的微观相互干扰现象,本文在Jiang模型基础上,引入车流占用面积可变项,提出一种新的各项异性的高速公路作业区宏观动力学交通流模型.
交通流运动首先满足车辆数目守恒定律,即连续性方程

在无汇合交织路段依然采用普通的各项异性模型,即
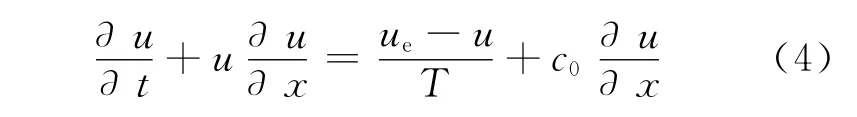
即没有引入占用面积可变项的各项异性的宏观动力学交通流模型.
在有汇合交织路段引入面积可变项式(2).这样,交织路段车辆流动的动量方程为

3.2 离散格式
采用有限差分方法进行数值模拟,连续性方程的离散采用适合交通流物理意义的差分格式为
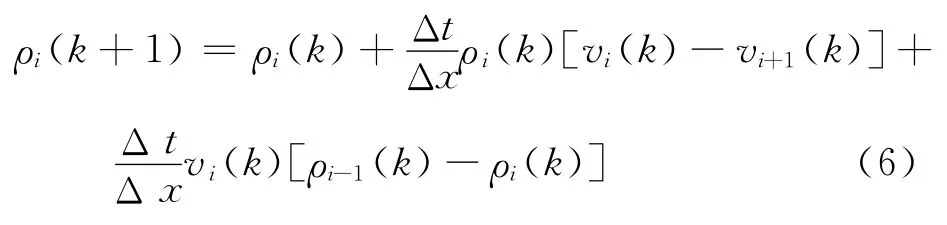
动力学方程采用一阶迎风格式离散,非汇合单元段的离散格式为
1)当路段密度较大时

2)当路段密度较小时
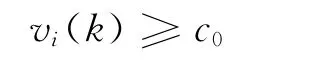

交织单元段的离散格式为
1)当路段密度较大时

2)当路段密度较小时
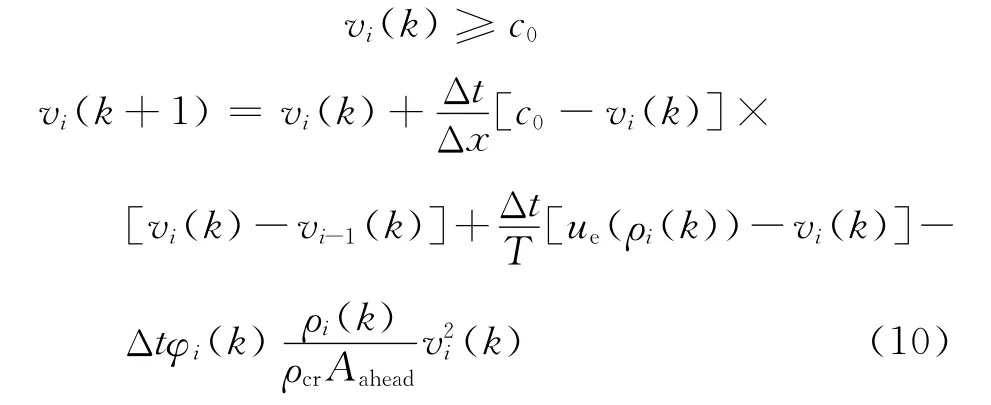
本文采用的平衡速度密度关系为

式中:i为单元段编号;k为时间间隔编号;Δt为仿真时间间隔;T 为松弛时间;vf和ρcr,i分别为第i单元段的自由流速度和临界密度;a和b为平衡方程的回归系数.
3.3 数值模拟
采用如下模拟路段,高速公路普通双车道路段10km,前方作业区因车道关闭形成的单车道路段10km,等距分成100网格,时间步长按计算稳定性要求确定,数值模拟采用的参数为:vf=90 km/h,双车道临界密度ρcr=150veh/km,单车道临界密度ρcr=75veh/km,T=5s,Δt=10s,c0=54km/h,a=0.5,b=2;交织区假设为第49和第50个单元段,采用改进的动量方程的离散格式,其他单元段采用普通路段动量方程的离散格式.
就以下2种Riemann初值条件进行数值模型,以考察交通流出现阻塞即阻塞车流得到疏导时的情况,也即考察该模型及其离散格式能否较好地处理交通激波及交通稀疏波的情况,也考察该模型能否正确模型交织区的交通拥挤现象.

式中:ρu和ρd分别指上、下游车流密度;1和2代表2种初值情况,第一种情况表示上游拥堵而下游畅通,第二种情况表示上游畅通而下游拥堵.数值模拟2种不同情况的目的在于理解汇合交通流模型是否能定性模拟不同情况下车流拥堵消散和传播的物理特性.
初值速度条件采用平衡速度

式中:vu和vd分别指上、下游车流速度,第一种初值条件计算结果见图1.可以看出,本文的汇合交通流模型可以产生稀疏波,而且汇合单元段也可产生高密度现象,这些都跟实际交通流特性一致.
第二种初值条件计算结果见图2.可以看出,本文的汇合交通流模型可以产生激波,而且汇合单元段也可以产生交织引起的高密度现象,这些也是跟实际交通流特性一致的.
4 结束语

图1 第一种初值条件下车流密度时空变化图

图2 第二种初值条件下车流密度时空变化图
在深入了解交通流运动学性质及其研究进展的基础上,得到了一种能够更好地描速高速公路交通流特性的各项异性的交通流模型,在微观分析高速公路作业区交通流的面积可变效应后,在普通路段的交通流模型中引入面积变化等效力项,进而提出了改进的高速公路作业区交通流模型.并给出了模型的离散格式.数值实验表明,模型可基本反映交通流的物理特性;在描述不均匀密度在车流中的传递,车道数目变化对交通流的影响方面,有一定的优势.
但是,本文仅限于初步的数值实验模拟,用来验证提出的高速公路作业区宏观动力学交通流模型的物理意义的合理性,下一步研究可结合我国城市的大通特点,设计实验,选择测点进行实测,以标定模型中参数,使模型较好地符合于实际高速公路作业区交通控制的工程实践.具体有以下几个方面值得进一步研究:(1)面积变化等效力项中参数的识别;(2)汇合交通交织段长度的研究;(3)模型中其他参数的现场识别的研究,如畅行速度、阻塞密度、调节时间.
[1]张 翛,蔡晓禹,孙立军.高速公路作业区交通流的运动学波分析[J].公路交通科技,2007,24(3):98-101.
[2]郭传乐.浅谈改善高速公路交通安全的有效方法[J].山西交通科技,2011(2):78-79.
[3]Richards P I.Shockwaves on the highway[J].Oper.Res.,1956(4):42-51.
[4]Pipes L A.Vehicle accelerations in the hydrodynamic theory of traffic flow[J].Trans.Res.,1969(3):229-234.
[5]Payne H J.A macroscopic simulation model of freeway traffic[J].Trans.Res.Rec.,1979,77(2):68-75.
[6]Papageorgiou M.A hierarchical control system for freeway traffic[J].Trans.Res.,1983(17B):251-261.
[7]薛 郁.交通流的建模、数值模拟及其临界相变行为的研究[D].上海:上海大学上海市应用数学与力学研究所,2002.
[8]Jiang R,Wu Q S,Zhu Z J.A new continuum model for traffic flow and numerical tests[J].Trans.Res.,2002(36B):405-419.
