M arkov模型在药物经济学中的应用
2012-04-09刘美娟刘玉聪孙利华
刘美娟,刘玉聪,孙利华
(沈阳药科大学工商管理学院,辽宁 沈阳 110016)
模型是决策分析的重要工具,用来综合一系列证据和不同来源的知识、数据。在药物经济学评价中运用模型技术,既可反映和概括所研究问题的基本特征,又符合现实,使决策分析变得更科学,其中常用的模型包括Markov模型、决策树分析、Monte Carlo模型。Markov模型在卫生领域的应用始于20世纪80年代,用于模拟慢性病的病程,20世纪90年代后逐渐应用到药物经济学研究中。其基本原理是利用某一变量的现在状态和动向,去预测变量未来的状态及动向,是国外最流行的用于药物经济学分析的模型[1]。Markov模型与其他统计方法如回归分析、时间序列等的不同之处是,它不需从复杂的预测因子中寻找各个因素之间的相互规律,只需考虑事件本身历史状况的演变特点,通过计算状态转移概率预测内部状态的变化[2]。在此着重介绍Markov模型在药物经济学中的应用。
1 M arkov模型
Markov模型是俄国数学家Markov建立的一种分析随机过程的方法。Markov经过多次试验最终发现,一个系统的状态转化过程中,第 n次转化获得的状态常决定于前1次(第 n-1次)试验的结果。对于一个系统,由一个状态转移到另一个状态的转化过程中,存在着状态转化概率,并且这种转化概率可以依据其紧接的前一状态推算出来,而与该系统的原始状态和此次转移前的过程无关[3]。一系列的Markov过程成为Markov链。Markov的基本方程为:
2 M arkov模型在药物经济学中的构建
Markov模型一般用于评估超过试验时间的长期成本和效益,与其他模型相比,能较好地反映疾病的过程,被认为特别适用于慢性疾病研究。它将疾病分成几个不同的健康状态(Markov状态),根据各个状态在一定时间内相互间的转换概率模拟疾病进程和结局,从而估计出疾病发展的结果与费用[4]。Markov模型在药物经济学中构建的基本过程见图1。

图1 Markov模型在药物经济学中构建的基本过程
Markov模型的健康状态:药物经济学评价中,Markov模型是由一组互斥的但又是完备的状态组成。互斥的是指任何两个状态不可能交叠,完备的是指模型中的状态包括了各种可能的状态,不存在任何别的状态。任一个体在某一时点必然处于某一个状态,并且只能处于一个状态。所有这些状态构成了一个状态空间。例如慢性丙型肝炎,可以分为7个状态,即轻度慢性丙型肝炎、中度慢性丙型肝炎、代偿性肝硬化、失代偿性肝硬化、肝移植、肝癌、死亡。
Markov模型健康状态的转移和循环周期:状态可能是时间维度上的变化,这称为状态的转移(transition),离散的Markov模型要研究在一系列的离散周期(cycle)中的状态转移。周期的长度与疾病的特征和要评价的干预/项目有关,可以是1年,也可以是1个月或是1周,等等。状态转移的概念也包括状态没有变化,即下一个周期中仍处于原来状态的情况。一般来说,在某一个周期,患者处于健康状态,在下一个周期中,可能仍然处于这个状态,也可能转移成更差状态,或者健康状态改善变为更好的健康状态。死亡状态是不可逆的,称为吸收态[5]。从一系列的健康状态开始,其过程可以用状态转化图来表示。图2是一个简单的Markov模型的例子,实际的Markov模型要复杂得多,多数疾病不止一种疾病状态,多种疾病状态之间可以相互转换。
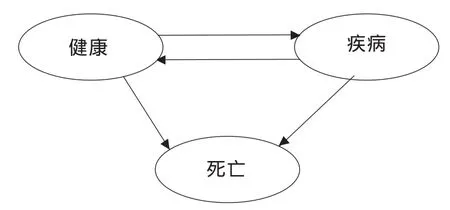
图2 某疾病的Markov简化模型
Markov的状态转移概率:任何一种治疗都存在不确定性,因此,由治疗所产生的健康状态转移是一种随机变化,或是只能以概率来表达这种变化,这就是转移概率(transition probability)。实际上,转移概率就是患者的Markov模型状态之间在一定周期长度下变化的速度。在下一个周期,从一种状态转变为其他状态(包括原来的状态)的转移概率之和必须等于1.00[6]。一般,Markov模型要求估计出各种状态的转移概率,从而得到一个矩阵,称为转移概率矩阵。一般形式如下:

它表示状态空间有 n种状态,P11表示第一种状态在下一个周期保持状态1的概率,P12转移为状态2的概率,等等。一般的Pij表示第 i状态转移为第j个状态的概率。因为第 n种状态一般为吸收态,所以Pn1,Pn2,...Pn,n-i都为0,而Pnn=1。若状态不可逆,则上述矩阵对角线以下的各个元素之和均为0。最简单的情形是这些转移概率在所有周期中都是相同的。一种复杂的情形是,在不同的周期转移概率各不相同。这些状态转移概率数据大多依靠医学文献、公共数据库或依赖专家的判断、观点来获取。
Markov各个健康状态的效用值和每个周期消耗的成本:在每一个状态下,都有一个成本和效用值(成本-效用分析)与之联系,药物经济学中的效用值多代表健康相关的生命质量。成本是实施一种干预手段所要消耗的资源价值,是直接成本、间接成本与无形成本之和。一般形式见表1。
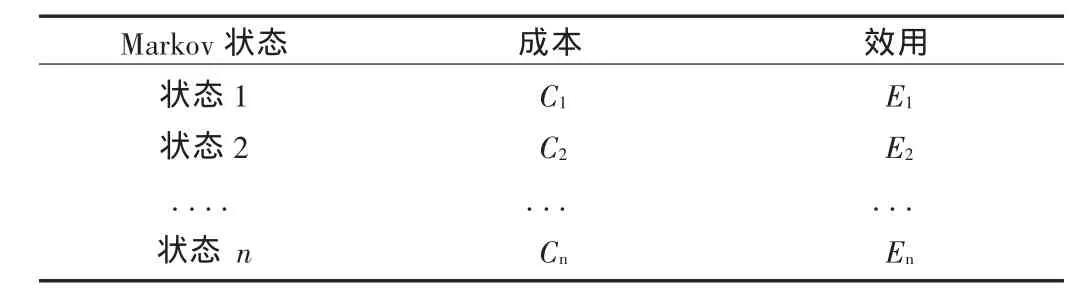
表1 Markov模型各个健康状态的效用值和成本
3 M arkov模型在药物经济学评价中的运算方法
首先把假设的患者队列分配给各初始状态,依据状态转移概率矩阵,计算出Markov模型循环周期的各个状态的分布数量;然后依据每一个状态下的成本和效用值,就可得到药物经济学中的评价指标[6]。
1)计算Markov模型的各个周期健康状态
已知初始状态,依据状态转移概率矩阵,就可以逐步计算出1个周期、2个周期直到 n个周期以后的状态。
设初始状态(即在第0个周期的状况)为 S0,
S0=(S10,S20...Sn0)
则第一个周期的状态 S1为
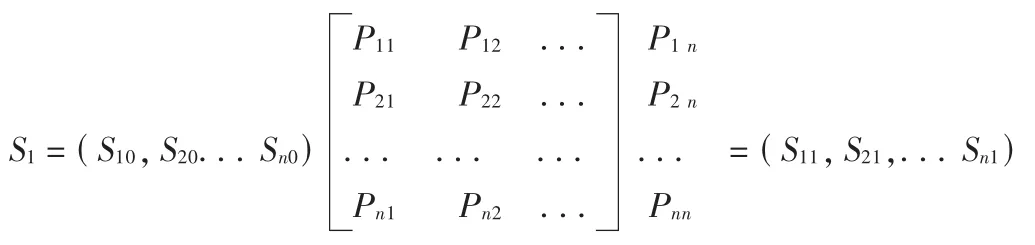
在第2个周期的状态S2为

即使不同周期的转移概率不同,但只要能知道各个周期的转移概率矩阵M1,M2,...,就比较易得到各个周期的状态。这时,只要把不同的概率矩阵带入计算公式就可以了。
2)获得药物经济学中的评价指标
计算出了Markov模型各个周期的健康状态,知道了Markov各个健康状态的效用值和每个周期消耗的成本,就可以估算每个阶段以及评价项目总周期的疾病治疗的成本、效果以及获得的QUAY的情况。具体计算方法如下。
在第1个周期,生命质量调整年的期望值为:
EF1=S11×E1+S21×E2+...+Sn1×En
周期成本的期望值为:
EC1=S11×C1+S21×C2+...+Sn1×Cn
同样,在第2个周期,这两个期望值分别为:
EF2=S12×E1+S22×E2+...+Sn2×En
EC2=S12×C1+S22×C2+...+Sn2×Cn...
在第T个周期,这两个期望值分别为:
EFT=S1T×E1+S2T×E2+...+SnT×En
ECT=S1T×C1+S2T×C2+...+SnT×Cn
这T个周期的累积效用和累积成本分别为:
EF累积=EF1+EF2+...+EFT
EC累积=EC1+EC2+...+ECT
4 结语
Markov模型用来估计疾病发展的时间进程以及治疗措施对患者健康状态的影响,依据每个健康状态和每个周期中患者的比例,估计每个阶段疾病治疗的效果、成本以及获得的QUAY的情况,在药物经济学模拟慢性病中具有广泛的实用性。
[1]张 洁,黄泰康.卫生经济学评价中马尔可夫系列模拟方法介绍[J].中国药物经济学,2008(4):36-41.
[2]吴 晶,黄泰康.马尔可夫模型及其在药物经济预测中的应用[J].中国药房,2006,16(14):1 049-1 050.
[3]陈 洁.药物经济学[M].北京:人民卫生出版社,2006:161-162.
[4]王 倩,金丕焕.Markov模型在卫生经济评价的应用[J].中国卫生统计,2000,17(2):86-88.
[5]毛正中.药物经济评价方法[M].北京:中国统计出版社,2009:274-276.
[6]Andrew Briggs,Mark Sculpher.An Introduction to Markov Modelling for Economic Evaluation[J].Pharmacoeconomics,1998,13(4):397-409.
