基于CATIA求圆锥与圆球相贯线的投影分析
2012-04-07潘子健孟祥宝潘淑璋
潘子健, 孟祥宝, 潘淑璋
(吉林大学机械科学与工程学院,吉林 长春 130025)
基于CATIA求圆锥与圆球相贯线的投影分析
潘子健, 孟祥宝, 潘淑璋
(吉林大学机械科学与工程学院,吉林 长春 130025)
分析了用辅助球面法和换面法求圆锥与圆球各种位置相贯线的投影作图过程,为辅助球面法的求解提供了较多的示例和思路,也为求复杂回转体交线的作图过程提供了借鉴,并通过CATIA三维模型佐证求解相贯线的正确性,进而使求解过程直观、准确、方便。
定心球面法;变心球面法;换面法;相贯线;工程图学;CATIA应用
求回转体表面的相贯线是工程图学课程投影基础部分较难理解的内容之一,其作图方法和过程有许多限制条件。通常有表面取点法、辅助平面法、辅助球面法、辅助柱面法和辅助锥面法等[1-6],前两种方法利用回转体某一投影的积聚性,后3种则要求相贯体之间及其对投影面有特殊相对位置。
相贯线是参与相交两立体表面的共有线,求相贯线投影的实质是求两立体表面上一系列共有点的投影。用辅助球面与相贯两回转体表面相交,当球心同时位于两回转体轴线时,所得交线是分别与其轴线垂直的圆,此两圆的交点就是相贯线上的点,即3面共点原理。基于此分析,只要两回转体轴线相交,就可以考虑使用辅助球面法求其相贯线。
换面法则是将不能在投影面上直接投影成圆或直线(其中包含相贯线上点),但通过向新投影面投影能够得到圆或直线(实形或实长),以便作出相贯线上点的方法。
1 用辅助球面法求相贯线
辅助球面法分为定心球面法和变心球面法两种。由于学时的限制,多数教材只简介定心球面法,变心球面法介绍很少。本文以圆台和圆球相贯为例,分析用定心球面法和变心球面法求解各种位置相贯线的具体作图过程。
1.1 用定心球面法求相贯线
用定心球面法求相贯线是指固定辅助球球心位置,改变辅助球半径与两曲面相交,交线是一系列圆的一种作图方法。
如图1上图所示,圆台轴线和圆球球心构成正平面,在正面投影中可以以圆台轴线与球体对称中心线的交点 O '为固定球心,依次作辅助球面(正面投影为a '、b '、c' 、d ')与圆台相交的水平纬圆分别为h '、e '、f '、g ',与圆球相交分别为侧平圆p '、k '、j '、i ';这些纬圆的正面投影均为直线,其中h '与p '、e '与k '、f '与j '、g '与i '分别相交于1 '、2 '、3 '、4 '点,即分别为辅助球面、圆台和圆球的3面共有点。加上圆台与圆球正面投影转向轮廓线的交点共有6个点,将其顺次光滑地连接起来,就作出了圆台与圆球的正面投影的相贯线,相贯线的另两面投影按照投影规律可以方便求出,这里不再赘述。图1下图是相应投影作图过程的CATIA三维模型。
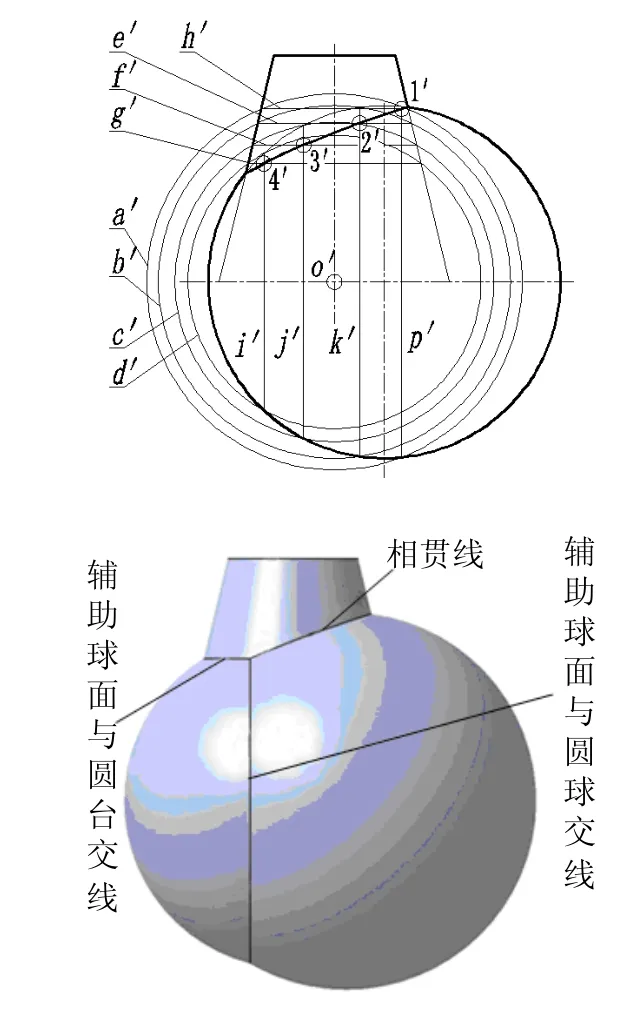
图1 球心和圆台轴线构成正平面的定心球面法投影作图之一
如图2上图所示,圆台与圆球的位置与图1一致。由于圆台轴线与圆球球心构成正平面,与无数条圆球的正平直径(轴线)相交,因此,也可以把辅助球面的固定球心取在圆台轴线的任一位置O'。取任意半径作辅助球面,在V面投影a '、b '、c '、d '与圆台相交的纬圆为h '、e '、f '、g ',与球体相交为纬圆p '、k '、j '、i ',这些纬圆的V面投影都是直线。h 'i '、e 'j '、f 'k '、g 'p'分别相交于1 '、2 '、3 '、4 '点,把这4个点加上圆台与圆球主视转向轮廓线的交点顺次光滑连接便作出相贯线的正面投影。图2下图是相应投影作图过程的CATIA三维模型。
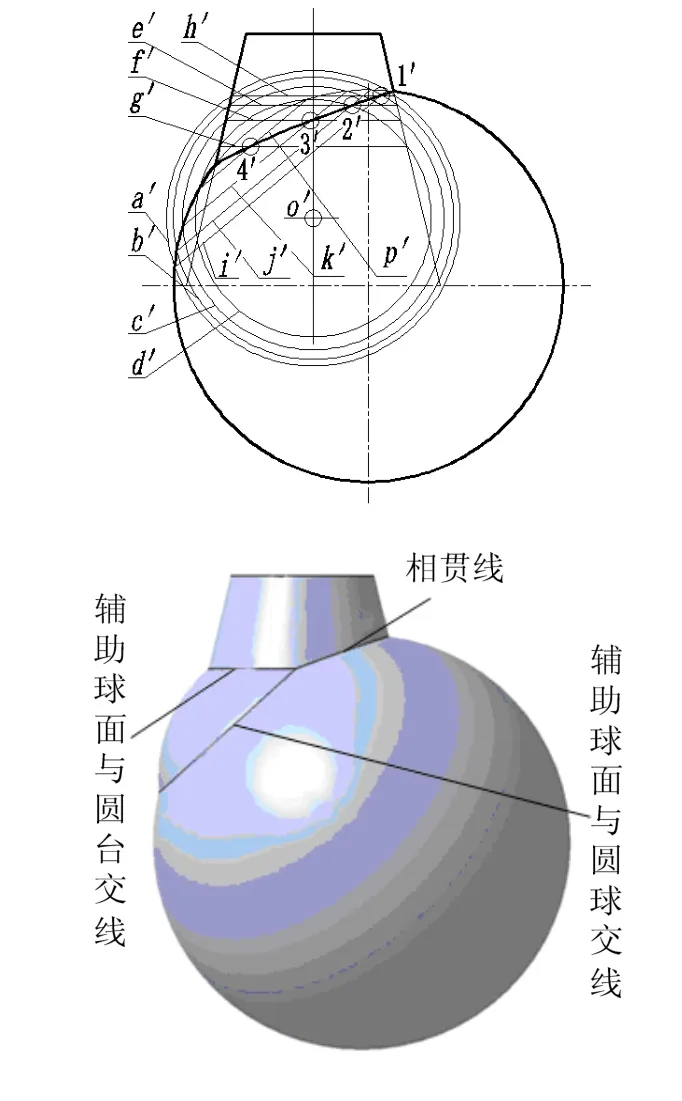
图2 球心和圆台轴线构成正平面的定心球面法投影作图之二
另外,当圆台轴线与圆球球心所构成的平面是铅垂面时,也可以把辅助球固定球心取在圆台轴线与过球心的水平面的交点O处,作图过程需要利用其两面投影,如图3上图所示。
以O点为固定球心作辅助球面,正面投影为a'、b ',水平投影为a、b,辅助球面与圆球交线的水平投影为e、f,与圆台交线的正面投影为c '、d ',根据c '、d '作出水平投影c、d,c与f的交点3、5;d与e的交点2、6为相贯线上的点,根据投影规律,利用纬圆求出这些点的正面投影2 '、3 '、5 '、6 ',再作出两个极限点1、1 '、4、4'(为使图面清晰作图过程省略),把这6个点顺次光滑连接起来即求出圆台与圆球体的相贯线的两面投影。图3下图是相应投影作图过程的CATIA三维模型。
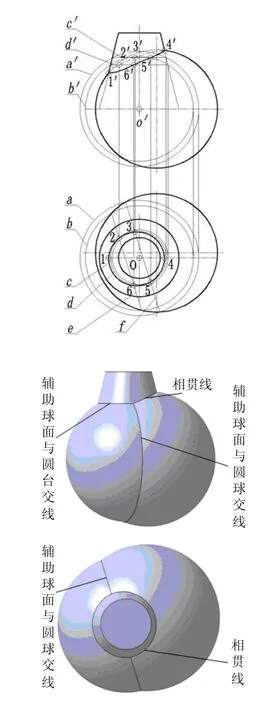
图3 球心和圆台轴线构成铅垂面的定心球面法投影作图
1.2 变心球面法求相贯线
简单地说,用变心球面法求相贯线是改变辅助球球心位置和半径大小,使之与两回转体表面交线是一系列圆的一种作图方法。
如图4上图所示,圆台轴线和圆球球心构成的平面为正平面。任取两段弦a '、c ',作弦a '、c '的中垂线,交圆台轴线于Ob'和Od',以Ob'和Od'为圆心画圆b '、d '与圆台的主视转向轮廓线交于e '、f ',a '、e '相交于2 '点,c '、f '相交于3'点,2 '、3 '这两个点即是相贯线上的点,再作出两立体主视转向线的交点1 '、4 ',把这4个点依次光滑连接便作出相贯线的正面投影(为使图面清晰仅作出两个一般位置点)。相应的CATIA三维模型如图4下图所示。
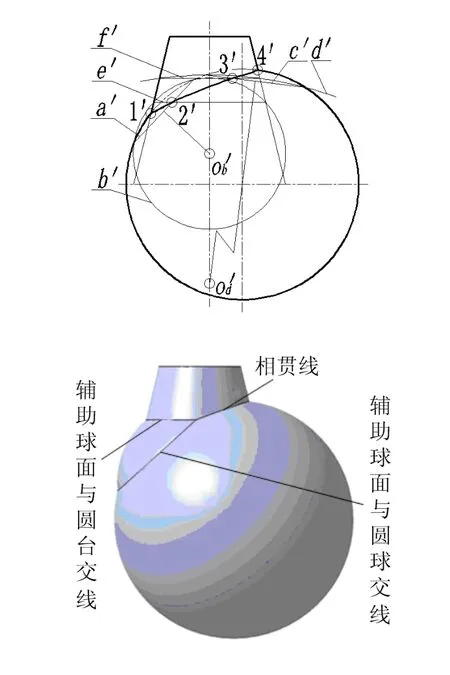
图4 变心球面法求相贯线投影作图之一
如图5上图所示,圆台与圆球的位置与图4一致。分别作正垂面pva、pvb、pvc与圆球相交,交线为正垂面内的纬圆,过O '分别作pva、pvb、pvc的垂线交圆台轴线于Oa'、Ob'、Oc',再分别以Oa'、Ob'、Oc'为圆心画圆a '、b '、c '与圆台转向轮廓线交于d '、e '、f ',它们与pva、pvb、pvc的交点为2 '、3 '、4 ',再作出圆台与圆球体主视转向轮廓线的交点1 '、5 ',将其顺次光滑连接便求出相贯线的正面投影。图5下图是相应的CATIA的三维模型。
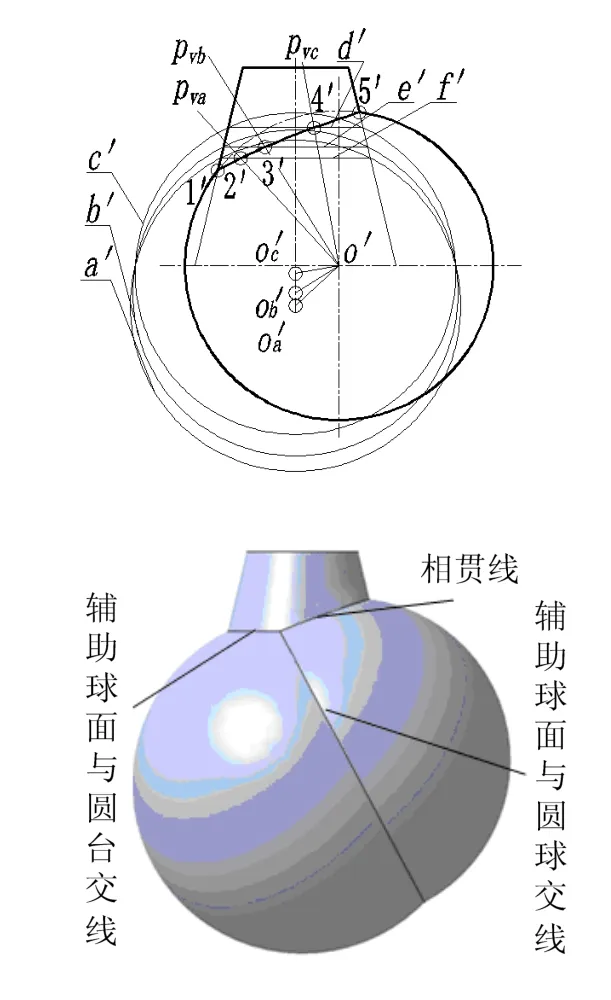
图5 变心球面法求相贯线另一种投影作图之二
2 用换面法求相贯线
以上用辅助球面法求相贯线都是在圆台轴线与圆球球心构成正平面或铅垂面前提下进行的,可以方便地用定心球面法或变心球面法。其中当圆台轴线和圆球球心在构成铅垂面时(见图3),球心只能取在圆台轴线与过球心水平面的交点处,这时用变心球面法求相贯线,辅助球面与两立体的交线在两个投影面的投影都不是直线或圆,无法直接作出相贯线,因此可以采用换面法,使新投影面与圆台轴线与圆球体球心构成的平面(即水平投影的对称平面)平行,作图过程如图6所示。

图6 用换面法求相贯线投影作图
在新投影面作球体投影的弦长a '、b '、c ',作a '、b '、c '的中垂线交圆台轴线于Oa'、Ob'、Oc',以Oa'、Ob'、Oc'为圆心画圆与圆台转向轮廓线相交于纬圆h '、i '、j ',此时a '、b '、c '和h'、i '、j '相交于2 '、(3 ')、4 '、(5 ')、6 '、(7 ')点,再求出相贯线的极限点1 '、8 ',在新投影面上把这些点光滑连接,就求出了相贯线在新投影面的投影。根据相贯线在新投影面的投影可以作出原投影面V、H的投影(作图过程略)。
3 结 束 语
通过以上作图过程可以看到利用辅助球面法求相贯线有其独特的优势,特别适用于复杂回转体相交的情况。本文的工作为复杂回转体相贯线的求解提供了一些方法、思路和借鉴。同时用CATIA三维模型为相贯线投影作图过程增强了直观性。
[1] 魏新贵. 辅助球面法应用条件的分析和讨论[J]. 江苏工学院学报, 1987, (4): 101-107.
[2] 鲁建慧. 用异心辅助球面法求作两曲面的交线[J].黑龙江矿业学院学报, 1994, (2): 61-64.
[3] 易原源. 辅助球面法应用于非回转面的分析和讨论[J].南方冶金学院学报, 1992, (2): 323-331.
[4] 大连理工大学工程画教研室. 画法几何学[M] . 北京: 高等教育出版社, 1992: 134-146.
[5] 合肥工业大学工程图学研究室. 画法几何学[M] .北京: 机械工业出版社, 1999: 116-124
[6] 同济大学, 上海交通大学. 机械制图[M]. 北京: 高等教育出版社, 1997: 130-131.
Projection analysis of intersection of cone and sphere based on CATIA
Pan Zijian, Meng Xiangbao, Pan Shuzhang
( College of Mechanical Science and Engineering, Jilin University, Changchun Jinlin 130025, China )
The projection construction process of intersection of cone and sphere in some spatial locations is analyzed by the auxiliary-sphere method and projection-transformation method. It provides several samples and some clues for the implementation of intersections of basic and complex rotational solids by auxiliary-sphere method. The correctness involved in above is verified by 3D hybrid modeling on CATIA software, in which it makes the construction process pictorial, perfect and convenient.
fixing-center sphere method; shifting-center sphere method; projectiontransformation method; intersection of geometric solids; engineering graphics; CATIA application
TH 126
A
2095-302X (2012)04-0020-04
2011-06-13
吉林省教育厅重点教研资助项目([2005]23号)
潘子健(1965-),男,吉林长春人,讲师,学士,主要研究方向为机械设计与理论、机械CAD。
