面向建筑物重建的相机标定方法研究

余 烨， 刘晓平， 徐 伟， 韩江洪

（合肥工业大学计算机与信息学院可视化与协同计算（VCC）研究室，安徽 合肥 230009）

面向建筑物重建的相机标定方法研究

余 烨， 刘晓平， 徐 伟， 韩江洪

（合肥工业大学计算机与信息学院可视化与协同计算（VCC）研究室，安徽 合肥 230009）

由于灭点具有很多独特的几何属性且大量地存在于建筑物场景中，因此针对建筑物重建，提出了一种基于灭点的相机标定方法。首先通过构造各种几何约束关系，如灭点与相机矩阵间的关系、世界坐标原点和相机矩阵间的关系，逐步实现相机矩阵的度量重建和欧氏重建，获得相机矩阵的值，然后通过分解相机矩阵得到相机的内外部参数。该方法在标定过程中无须借助任何标定物，求解过程简单，标定速度快。实验结果表明，该方法可以满足虚拟现实中建筑物场景重建的需要。

基于图像的建模；计算机视觉；灭点；相机矩阵；针孔相机模型

三维重建技术是计算机视觉、人工智能、虚拟现实等前沿领域的研究热点和难点，是人类在基础研究和应用研究中面临的重大挑战之一。城市场景中的建筑物重建在城市规划、灾害仿真及评估、地图绘制、无线网络规划、虚拟导游等领域都具有广泛的应用，是一项十分具有挑战性的工作。根据数据源的不同，建筑物重建可以分为基于图像的重建[1]和基于点云的重建两大类。

由于图像是普遍存在且最容易获取的一种数据源，因此基于图像的建筑物重建受到了广大研究者的青睐。对于大多数基于图像重建的任务而言，首先应对图像进行标定，以便确定在每一幅图像的拍摄过程中照相机相对于三维场景的方位和取景参数，即确定相机的内、外参数[2]。相机标定是计算机视觉领域研究的一个重要课题，也是基于图像重建中重要的一步。

空间上的一组平行线经过透视投影成像后，在成像平面上交于一点，称为灭点。由于灭点具有很多可以利用的属性[3]，且大量地存在于建筑物场景中，因此，本文利用灭点来进行相机的标定，提出了一种面向三维重建的相机标定方法。该方法利用灭点的几何属性，推导出灭点和世界坐标系原点在图像中的投影与相机矩阵之间的约束关系。利用这些约束关系，对相机矩阵的自由度进行约束，结合灭点的在三维空间中的性质，实现相机矩阵在度量重建和欧氏重建上的标定。由于本文所提出的相机标定方法无需加入任何其它的限制条件，采用的是线性方法，因而具有计算过程简单、标定速度快等优点，满足虚拟现实领域中对建筑物重建的需要。

1 相关研究

在相机标定方面的研究有很多，根据其标定方法的不同大体可以归结为两类：传统的标定方法和自标定方法[4]。传统的相机标定方法需要借助于标准参照物，利用参照物与图像间的对应关系来确定相机模型的参数。这类方法的优点是对相机模型没有限制，具于很高的标定精度；其缺点是标定过程复杂，需要高精度的已知结构信息。由于在建筑物重建的实际应用中，无法使用标定块，因而不能使用这类方法。

不同于传统的标定方法，自标定方法不需要利用标准参照物，即不需要知道准确的三维度量信息，而是试图利用多视图的几何关系，求解基本矩阵，进而计算相机模型的参数。这使得在线、实时地计算相机参数成为可能，同时也带来了一系列问题，如：得到的解不唯一；在图像中含有噪声时，解的值与实际值偏差较大，即解不稳定。如果不借助标准参考物，基于灭点的相机标定方法属于自标定的范畴，这种方法被广泛地应用于三维重建领域。

20世纪 90年代初，B.CAPRILE 和 V.TORRE 首次提出了基于灭点进行相机标定的思想，并总结、证明了灭点的若干几何属性。文献[6]提出了一种基于两个灭点估算相机内、外部参数的方法，该方法的前提是灭点存在、主点位于图像的中心、像素长宽比固定。由于在对相机内参数进行估算时没有充分利用灭点的属性，因而计算过程稍显复杂。文献[7]在对灭点几何属性进行研究的基础上，借助于正方形像素标定物，对相机模型进行了标定，同时利用非线性优化方法对计算结果进行了优化。由于借助了标定物，因此该方法在场景重建中的应用受到了限制。文献[8]提出了一种基于灭点的物体长度测量方法，该方法利用灭点来计算相机的内部参数，通过得出与参考平面垂直的两物体长度之间的比率与相机内部参数的关系，计算物体的实际长度。该方法能在给定两幅未标定图像，且图像平面上只有极少的几何信息的情况下，计算出物体在三维空间中的实际长度，但限定条件严格，要求已知参考面上一条已知直线的投影，以及与此直线正交的灭点。

在国内，基于灭点进行相机标定和建模方面的研究也很多。文献[9]提出了一种利用单个空间平面矩形，结合透视图像的几何属性，求解相机内外部参数的方法。由于在实际使用时相机在图像上的投影并不一定在图像的中心位置，因此在实际使用中该方法会造成一定的误差。文献[10]基于假想的世界坐标系，基于灭点的属性进行了相机的标定，并基于两幅图像进行了物体的重建，但由于忽略了比例参数，会造成计算结果的不稳定。文献[11]利用灭点属性推导出相机中心在世界坐标系下坐标位置的解析表达式，结合两幅图像之间的空间几何约束关系，从空间约束关系中反算出物体各点的空间位置，从而重建出物体几何模型。此方法中，并没有计算相机的外部参数，且对灭点的位置关系存在一些约束。

2 基于灭点的相机标定方法

2.1 焦距和主点的计算

不妨假设图像中 3个主方向的灭点分别为U、V、W，其齐次坐标分别为(u1, u2, 1)T、(v1, v2, 1)T、 (w1, w2, 1)T，其对应的空间齐次坐标为(1, 0, 0, 0)T、(0, 1, 0, 0)T、(0, 0, 1, 0)T。根据文献[5]中提出的灭点的属性“空间3条两两正交直线形成的灭点组成的三角形，其垂心即为相机光轴与成像平面的交点”，则△UVW的垂心即为主点，记为K，其在图像上的像素坐标为 (k1, k2, 1)。记相机的焦距为 f，则根据灭点的属性“与空间3条两两正交直线形成的灭点相关的单位向量也两两正交”[4]，得到

通过上式可以计算出焦距f。

2.2 几何约束关系的推导

点在世界坐标系中的坐标和在图像上坐标间的对应关系可以用下式来表示

其中(x, y, z, 1)T为点在世界坐标系中的齐次坐标，(s, t, 1)T为点在图像上的齐次坐标。由上式可以看出，相机矩阵Pc一共有11个自由度。根据线性代数的知识，求解含有 11个未知量的方程，需要 11个相互独立约束条件才可以得到线性解。因此，本节将讨论如何确定这 11个相互独立的约束关系。

1） 灭点和相机矩阵间的约束关系

将 U点的世界齐次坐标和图像坐标代入式(1)，得到

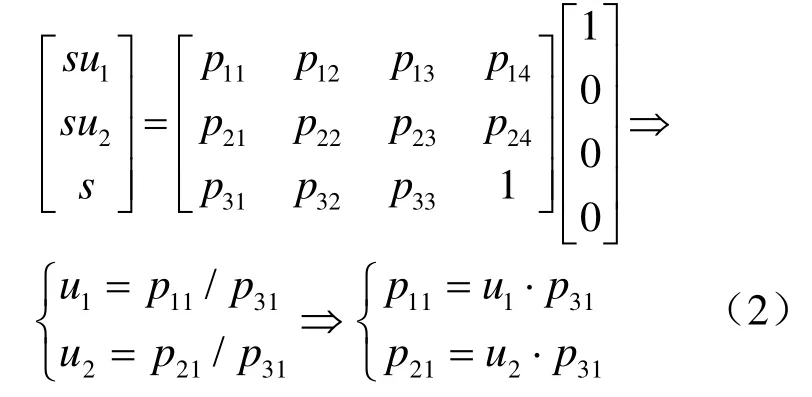
同理，将灭点V和W的世界齐次坐标和图像坐标分别代入式(2)，可以得到

式(2)～(4)表示了主方向灭点的图像坐标和相机矩阵之间的约束关系。从中可以发现，相机矩阵隐含着3个主方向灭点的像素位置，即给出用式(1)所表示的相机矩阵后，就可以利用本节推导的约束关系，得到该图像上3个主方向灭点在的像素齐次坐标，分别为

2） 世界坐标原点和相机矩阵间的约束关系

设世界坐标原点在图像上的投影点为P，图像坐标为(p1, p2)T，由于该点为世界坐标原点，所以其对应的空间齐次坐标为(0,0,0,1)T，代入式(1)得

同样可以发现相机矩阵隐含着世界坐标原点的像素位置，即给出用式(1)所表示的相机矩阵后，就可以利用本节推导的约束关系，得到该图像上世界坐标原点的像素位置为(p14, p24, 1)T。将式(2)～(5)代入式(1)，可以得到相机矩阵的改写形式

上述的3个灭点和世界坐标一共可以列出如式(2)～(5)所示的8个方程，即新增了8项约束条件，因此，相机矩阵的自由度由原来的 11个减少到了3个，即式(6)中所示的p31、p32和p33。

3） 作辅助线引入新的约束

如图1所示，在图像上做辅助线PU、PV和PW。则世界坐标X、Y、Z轴上的空间点在图像上的像素位置分别在直线PU、PV和PW上。在PU、PV和PW上各选一点，记为A、B、C，设其图像齐次坐标分别为(a1, a2, 1)T、(b1, b2, 1)T、(c1, c2, 1)T；并设A、B、C对应的世界坐标分别为X、Y、Z轴上的A'、B'、C'三点，则可以认为A'、B'、C'三点的世界齐次坐标为 (α,0,0,1)T,(0,β,0,1)T, (0,0,ε, 1)T。

图1 相机空间几何约束关系

将A点的空间齐次坐标和图像坐标代入式(1)，得

从式(7)中可以解出 p31α，记

同理，将B点和C点的空间齐次坐标和图像坐标代入式（1），可以解出 p32β、p33ε，记

4） 平行于世界坐标轴方向的线段之间的比例

本小节用来计算平行于主灭点方向，且含有公共顶点的线段之间比例。如图1所示，P '为世界坐标原点，P为世界坐标原点在图像上的所成的像，在图1上过P点作平行于X、Y、Z轴的辅助线，分别交OA、OB、OC于A1、 B1、 C1点。则由△ OPA1～△ OP 'A'、△ OPB1～△ OP'B'、△OPC1～△ OP 'C'可以得到

则

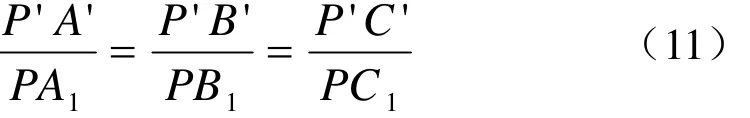
由余弦定理得

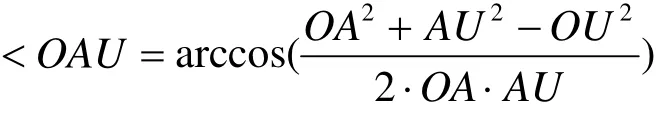
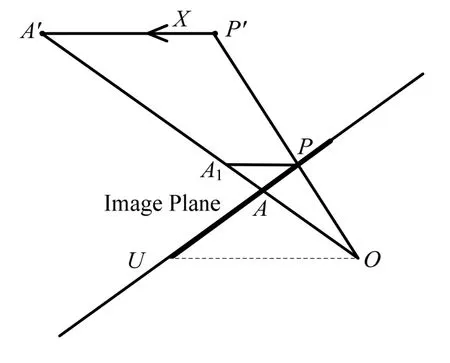
图2 PA1与 P 'A'的长度比例示意图

由于 U是 X方向的灭点，所以OU // P'A'/PA1，进而得到

由正弦定理，可以求出

同理可以求出

将式(12)～(14)代入式(11)，可以得出平行主灭点方向含有公共顶点 P'的线段 P 'A'、 P 'B'、P 'C'之间的比例关系

5） 相机矩阵的度量重建

设上步中计算得出

P'A':P'B':P'C'= α: β:ε=1:r1:r2则可以在相差一个相似变换的基础上重建出该矩阵。将α、β、ε的值等比例记为1、 r1、 r2，代入式(8)～(10)得

则相机矩阵的形式可以确定为

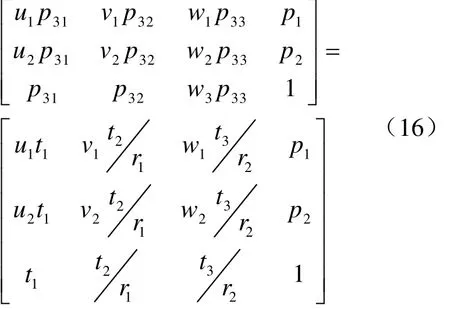
得到了3条空间线的比例关系，等价于又增加了两项约束，经此步后相机矩阵只剩下一个自由度，即在相差一个比例约束条件下，已经完成了标定。此步得出的相机矩阵是在度量空间上的重建，如果直接将此机矩阵用于三维重建，则求出的坐标和现实坐标相差一个固定的比例变换。

6） 相机矩阵的欧氏重建

由于在虚拟现实系统中的建模，只需要模型尺寸的比例关系正确即可，不需要得到具体的尺寸信息，因此，可以假设 P 'A'的长度为 lpa，这样最后一个自由度也被确定了下来。则可以得到P 'B'、 P 'C'的长度为r1⋅lpa、 r2⋅lpa。代入式（8）～（10）得到相机矩阵中

p33= t3r2⋅lpa，则相机矩阵的形式可以确定为

通过最后一个比例约束，相机矩阵的 11个自由度都被确定了下来，从而得到了我们所需要的解。此相机矩阵可以直接用于基于图像的重建中，如果需要进一步求解相机参数，可以采用对此矩阵进行分解的方法获得。

7） 相机内外部参数的确定

在此步骤中，对相机矩阵进行分解，以确定相机的内外部参数，实现相机的标定。首先，对相机矩阵进行变化如下

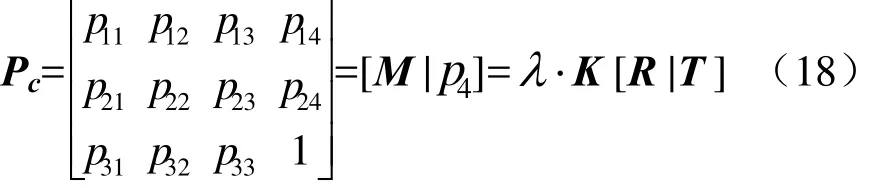
其中M为相机矩阵Pc的左三列所组成的矩阵，p4为相机矩阵Pc的第4列数值的列矩阵，K为相机内参数矩阵，T为相机平移矩阵，R为相机旋转矩阵

λ为非零的比例因子。

所以由式(18)可以得到 M =λ⋅KR，由于 R是正交矩阵、K为上三角矩阵，所以对于上式可以利用QR分解法得出内参数矩阵K、旋转矩阵R及比例因子λ。由 p4= λ⋅KT，可以求出旋转矩阵T。由此，可以确定相机的内外部参数。

3 实验结果与分析

首先，对该方法的有效性进行分析。

利用本文中提出的相机标定算法来求解相机矩阵，结合针孔相机模型[12]，对图像上建筑物的三维空间信息进行还原，从而实现建筑物的重建。由于本算法是基于灭点理论的，且需要保证图像中有3个两两垂直方向的灭点存在，因此，在拍摄图像时，需要保证建筑物的面不能和投影平面平行。以合肥工业大学图书馆为例，对其进行重建，如图3所示：(a)、(b)为源图像，(c)、(d)为重建后的效果。用A、B、C、D等对建筑物各顶点进行标注（如图3(a)所示），可以看出，目标图像和源图像上各点的位置关系相同。因此，该算法能恢复物体上各点之间的位置关系。

以AD的长度为基准，记为1，计算实际建筑物上各边的比例长度l1及重建后建筑物各边的比例长度 l2，并进行比较，计算其误差率从表1中可以看出，重建后物体上各边的比例长度和实际物体的基本相同。因此，此算法可以恢复场景中物体的长度比 例关系。

图3 合肥工业大学图书馆的重建

表1 建筑物中各边的长度比值

其次，对该方法的鲁棒性进行分析。

采用分辨率为1024×768的图像进行实验，首先计算出相机矩阵，然后对该相机矩阵分解得出相机的内外参数。通过3组实验，得到3组不同的相机内参数( fx、fy、s、u0、v0)和外参数(θx、θy、θz、tx、ty、tz)的值，如表2所示。然后对象素点加入零均值高斯噪声，进行扰动，噪声级从0.0像素开始，以0.2像素的步长均匀增加到2.0像素，在每个噪声级上进行 1000次试验，计算出相机的内外参数的均值和标准差（其中，内参数焦距的均值和标准差的变化情况如图4所示）。实验结果表明，本文提出的相机标定方法在噪声增大时，也可以得到比较好的结果，即该方法对图像上的噪声具有一定的鲁棒性。

表2 相机的内外参数

图4 实验结果

4 结 束 语

基于灭点的相机标定方法克服了传统标定方法中需要借助于定标参照物来进行相机标定的限制，在虚拟现实系统中具有很大的实用价值。本文利用灭点的属性，推导出一系列几何约束关系，如：灭点、世界坐标原点的像素位置和相机矩阵之间的约束关系等，在此基础上，提出了一种在单幅图像上利用灭点进行相机标定的方法。在标定过程中，通过引入新的约束，不断限制相机矩阵的自由度，从而完成了相机矩阵的在度量空间和欧氏空间下的重建，最后通过分解相机矩阵得到相机的内外部参数。由于采用的是线性的方法，因为具有计算过程简单、标定速度快等优点，可以满足虚拟现实系统中建筑物重建的需要。

为了实现三维复杂建筑物场景的重建，本文的进一步研究方向是研究具有球形、柱形或一些不规则形状的复杂建筑物存在时，其场景的恢复和真实感重建。

[1] 束 搏, 邱显杰, 王兆其. 基于图像的几何建模技术综述[J]. 计算机研究与发展, 2010, 47(3): 549-560.

[2] 刘 钢, 彭群生, 鲍虎军. 基于图像建模技术研究综述与展望[J]. 计算机辅助设计与图形学学报, 2005, 17(1): 18-27.

[3] 余 烨, 刘晓平. 基于灭点的三维物体重建[J]. 系统仿真学报, 2008, 20(15): 4069-4072．

[4] 邱茂林, 马颂德, 李 毅. 计算机视觉中相机定标综述[J]. 自动化学报, 2000, 26(1): 43-55.

[5] Caprile B, Torre V. Using vanishing points for camera calibration [J]. International Journal of Computer Vision, 1990, (4): 127-140.

[6] Guillou E, Meneveaux D, Maisel E, et al. Using vanishing points for camera calibration and coarse 3D reconstruction from a single image [J]. The Visual Computer, 2000, 16: 396-410.

[7] Liu Ying, Wu Yuanxin, Wu Meiping, et al. Planar vanishing points based camera calibration [C]// Proceedings of the International Conference on Image and Graphics, 2004: 460-463.

[8] Foroosh H, Cao Xiaochun, Balci M. Metrology in uncalibrated images given one vanishing point [C]// IEEE International Conference on Image Processing, 2005: 361-364.

[9] 袁国栋, 秦开怀, 胡 伟. 基于单幅透视图像确定相机参数的几何方法[J]. 计算机研究与发展, 2006, 43(11): 1933-1938.

[10] 余 烨, 罗月童, 等. 一种基于灭点的相机标定方法[C]//计算机技术与应用进展2007, 2007: 66-70.

[11] 刘晓平, 徐 伟, 余 烨. 一种基于双幅图像的物体三维重建[J]. 中国图象图形学报, 2009, 14(7): 1453-1457.

[12] 刘培珺, 石教英, 孙 鑫. 基于平面的建筑物表面模型重建算法的研究[J]. 计算机辅助设计与图形学学报, 2004, 16(8): 1045-1050.

Research on camera calibration used for building reconstruction

Yu Ye, Liu Xiaoping, Xu Wei, Han Jianghong
( VCC Division, School of Computer & Information, Hefei University of Technology, Hefei Anhui 230009, China )

Vanishing point has many geometry attributes and exists abundantly in building scenes, based on this, a camera calibration method is proposed using vanishing points, which is especially used for building reconstruction. Lots of geometry constraints are discovered, such as the constraint relationship between vanishing points and camera matrix, the origin of world coordinate system and camera matrix. Then through matrix reconstruction and Euclid reconstruction, the camera matrix is calculated. Through decomposition of this matrix, the inner and outer parameters of the camera are achieved. In this method, no calibration object is needed; besides, it also has the advantage of simple calculation process, high calibration speed. Experiments show that it can meet the needs of building reconstruction in virtual reality system.

image based modeling; computer vision; vanishing point; camera matrix; pinhole camera model

TP 391.9

A

2095-302X (2012)04-0076-07

2010-11-16

国家自然科学基金资助项目（61070124）；安徽省自然科学基金资助项目（11040606Q43）；中央高校基本科研业务费专项资金资助项目

余 烨（1982-），女，安徽安庆人，讲师，博士，主要研究方向为建模、虚拟现实与可视化。