深水钻井船波浪载荷预报

郭兴乾

（中国船舶及海洋工程设计研究院 上海 200011）

深水钻井船波浪载荷预报

郭兴乾

（中国船舶及海洋工程设计研究院 上海 200011）

以两艘钻井船为例，分别计算其波浪载荷传递函数和波浪载荷长期预报值，将计算结果与规范计算值比较，且对其中一艘钻井船计算其不考虑月池开孔时的波浪载荷预报，试图找出钻井船与常规船型的差异，为结构设计人员在钻井船设计方面提供一定的借鉴。

钻井船；波浪载荷；长期预报

0 引言

钻井船在其寿命期内遭受的外力主要有结构自重、环境载荷、作业载荷和偶然性载荷，环境载荷分波浪载荷、风载荷和流载荷。对船体结构强度而言，环境载荷中的波浪载荷最复杂且最关键。波浪载荷的确定，对钻井船强度评估起着关键的作用［1］。

通过对常规船舶波浪载荷的研究，国际船级社协会（IACS）给出建议公式，以计算波浪载荷沿船长方向产生的波浪弯矩和波浪剪力。对于非常规船舶，波浪载荷的预报主要依据数值预报和模型试验两种技术手段。模型试验由于周期长、费用高，故难以普遍应用。数值预报波浪载荷是借助于水动力分析理论及分析软件，完成船体任意剖面处波浪载荷的预报。

本文旨在通过三维水动力理论，对两艘钻井船进行波浪载荷直接预报。将计算结果与规范计算值进行比较，且对其中一条钻井船计算其不考虑月池开孔时的波浪载荷，从而找出钻井船与常规船型的差异，为钻井船的前期设计与快速反应提供一定的借鉴。

1 波浪载荷计算原理和方法

波浪载荷由波浪运动产生，而波浪运动是由许多具有随机相位的规则波叠加而成。因此，船在随机不规则波中的响应由单位波幅波中的响应（传递函数）和波浪谱来确定。

水动力分析中，通常假定浮体所处的海洋是均匀、不可压缩、无粘和无漩的理想流场。按照流场的简化程度，可分为二维切片理论、二维半理论以及三维水动力理论，其中以二维切片理论和三维水动力理论在工程上应用最为广泛。切片理论建模简单、计算效率高，但计算精度相对较低。三维水动力理论基于三维线性势流理论，适用于任意形状的船舶和海洋结构物。其计算精度高，能够获得较二维切片理论更为精确的湿表面水动压力分布［2］。

1.1 规则波中船体运动与载荷计算

规则波中以任意航向定速航行的船舶在时刻的六个自由度的位移为：

式中：ηi为1，2…6；

αi为位移幅值；

ω0为遭遇频率；

φi为相位角。

遭遇频率由航速V、浪向角β、波浪频率ω等确定。

六个线性耦合的运动微分方程为：

式中：Mjk为船舶的广义质量矩阵；

Ajk为附加质量矩阵分量；

Bjk为势流阻尼矩阵分量；

Cjk为静力复原矩阵分量；

Fj为扰动力幅值；

求解此方程，即可得出六个自由度的运动。由此可进一步求出船体某一剖面上的波浪诱导载荷。与船体运动的表达式类似，t时刻船体某一剖面的波浪载荷为：

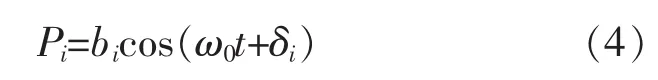
式中：i=1，2…6。

1.2 不规则波中船体运动与载荷计算

一般情况下，海面上的波浪不是规则波，它通常表现为随机的不规则波，所以应采用概率统计的方法计算波浪诱导的船体运动及波浪载荷响应［3］。

首先应求出波浪诱导船体运动和载荷的传递函数，然后通过船舶航行海区的海浪谱计算出船体波浪运动和载荷的响应谱，最后用波浪统计预报方法得出船体波浪运动和载荷的统计值，波浪统计预报方法分为短期预报和长期预报。

1.2.1 短期预报

短期海况可视为均值为零的平稳正态随机过程。此时船体对波浪的响应，可看作是线性时不变系统。由随机过程理论可知，在海浪的作用下（输入），其响应——波浪载荷（输出）亦将是均值为零的平稳正态随机过程。输入与输出之间关系可以通过以下公式给出［4］：

式中：Sζ（ω，H1/3，Tz，θ）为海浪谱密度；

SW（ω，H1/3，Tz，V，β+θ）为波浪载荷（可以具体是垂向波浪弯矩与剪力等）的谱密度，也可称为响应谱密度；

H（ω，V，β+θ）为系统传递函数（又称频率响应函数）的模，常称为幅频特性、响应幅算子、或增益因子，其值为单位规则波幅下的载荷响应幅值；

ω为波浪圆频率；

V为航速；

θ为组合波与主浪向的夹角；

β为航向角；

H1/3为有义波高；

Tz为波浪的特征周期。

对于一个均值为零的平稳正态随机过程，在窄谱（窄谱系数小于0.4）假定下，其幅值X服从Rayleigh分布。对应的概率密度为

式中：E为2倍的波浪载荷方差m0

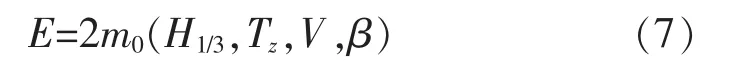
相应的概率分布函数为

如果给定一个超越概率，可以计算出此概率下相应的响应值。

由谱密度函数的性质及式（5），可知方差m0为

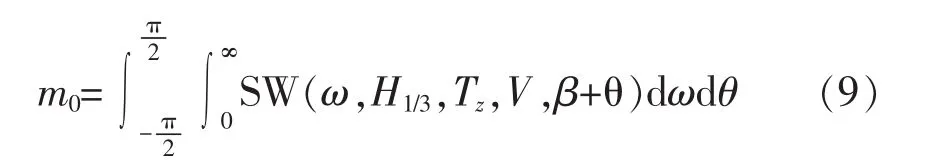
1.2.2 长期预报

长期预报通常是对一种或者几种典型的装载状态分别进行。因此，在给定的装载状态下，输入变量是海况、航向角和航速。

由短期预报可知，在海况为（H1/3，Tz）i中，船舶以航向角βi为航速Vk运行时，其波浪载荷幅值X大于某个可能值x0的概率，即Rayleigh分布函数

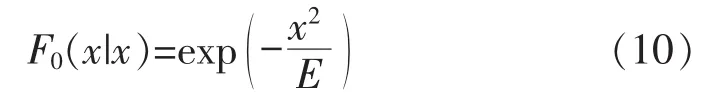
波浪诱导运动和载荷可以看作是很多短期Rayleigh分布的总和，并且由各种不同海况、不同航行状态所组成的短期分布彼此相互独立。那么，长期概率分布将是各短期概率分布的加权组合，即波浪载荷幅值X大于某一定值x0的超越概率为

因为航速对线性波浪载荷影响不大，故计算时V可取为定值，即航速出现的概率pk（V）=1。海况出现的概率pi（H1/3，Tz）取决于船舶实际运行海域的海浪统计资料。航向角出现的概率pj（β）按在0°~360°之间均匀分布的原则确定。通常规定船舶一生中遭到的波浪载荷循环数n=108，计算时可以取概率水平为

如果作业海域不定，那么一般推荐使用北大西洋波浪散布图，该图覆盖了北大西洋最危险的第8、9、15、16号海区。在进行变量的长期统计预报时，以超越概率10-8水平所对应的统计值作为设计值，该值大致对应于20年一遇波浪的设计值。

2 计算实例

2.1 波浪载荷计算

本文以两艘不同尺度钻井船为例，分别进行波浪载荷直接计算，两船主尺度见表1。

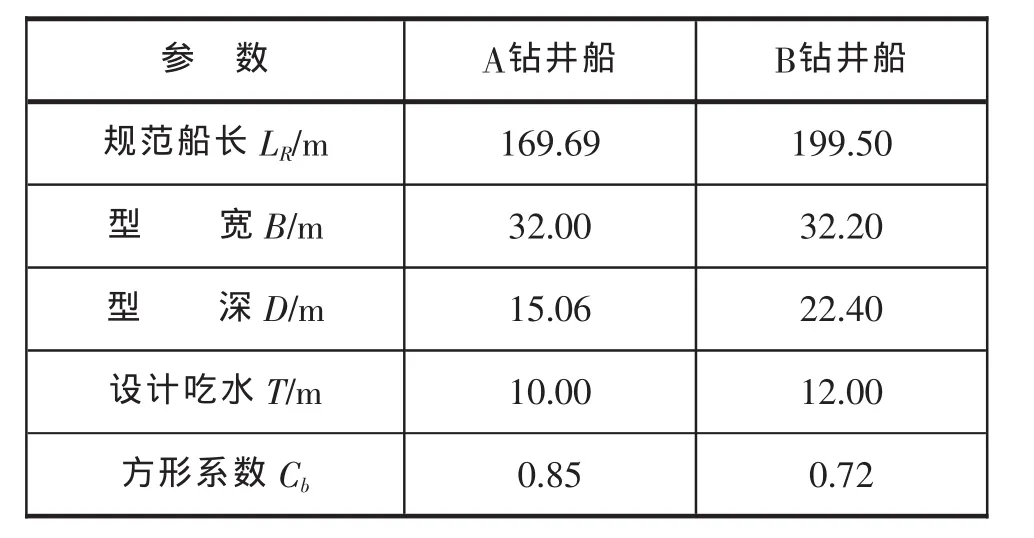
表1 钻井船主尺度

计算采用DNV船级社开发的SESAM/WADAM［5］和SESAM/POSTRESP［6］程序。该程序基于三维绕辐射势流理论，完成两艘钻井船的运动响应与波浪载荷预报。根据钻井船的几何外形尺度以及质量分布，建立钻井船的水动力模型和质量模型。图1和图2分别为A钻井船的质量模型和水动力模型。根据需要校核的剖面位置，选取了21个剖面位置进行波浪载荷计算预报。考虑B船为国外公司的设计专利技术，本文仅在后面列出其波浪载荷预报结果，以便结构设计人员参考。

图1 A钻井船质量模型

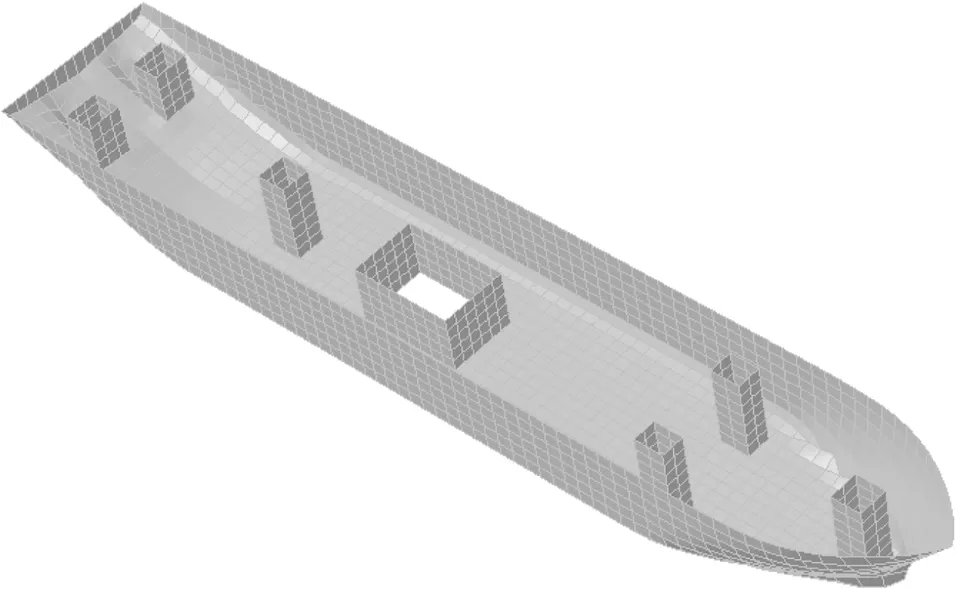
图2 A钻井船水动力模型

A、B两船作业海域不确定，因此选取北大西洋波浪散布图进行长期预报，超越概率取为10-8（20年一遇），波浪谱选用P-M谱。

计算中，浪向角取0°~180°，间隔15°等概率作用在船体上。频率范围为0.05~2.0 rad/s，间隔0.05 rad/s。

2.2 波浪载荷预报结果

通过计算结果可以看出：A钻井船在11号剖面处的垂向波浪弯矩最大（下文中，波浪载荷均指垂向波浪载荷）；B钻井船在11号剖面处垂向波浪弯矩最大。A、B钻井船波浪载荷预报结果分别见下页表2及表3。

2.3 波浪载荷预报值与规范计算值比较

为了直观显示两艘钻井船的直接预报值和规范计算值［7］的差异，故采用图表的方式列出两种方法计算的结果，如图3~图6所示。

表2 A钻井船波浪载荷预报值

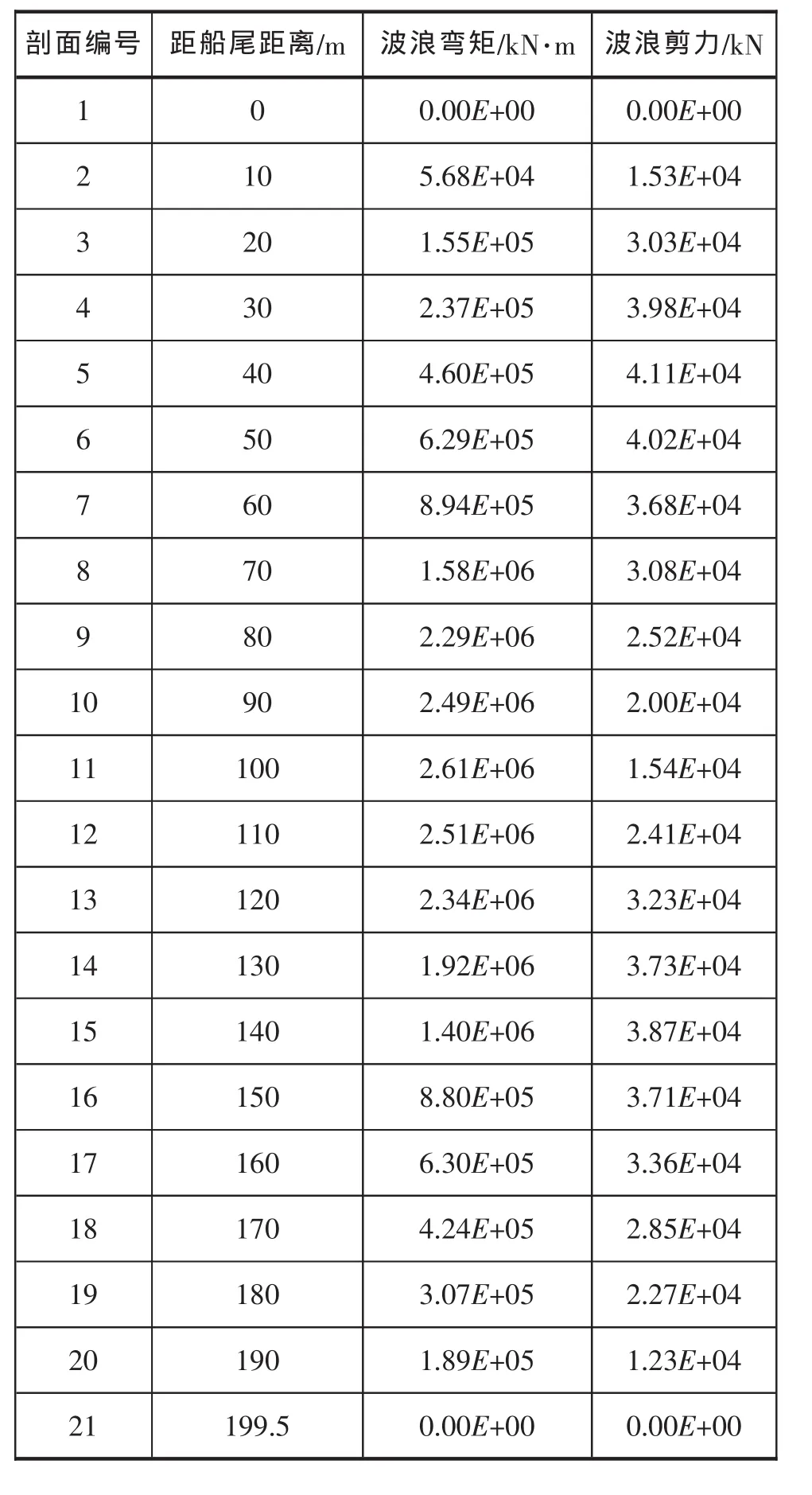
表3 B钻井船波浪载荷预报值

图3 A钻井船波浪弯矩预报值与规范值

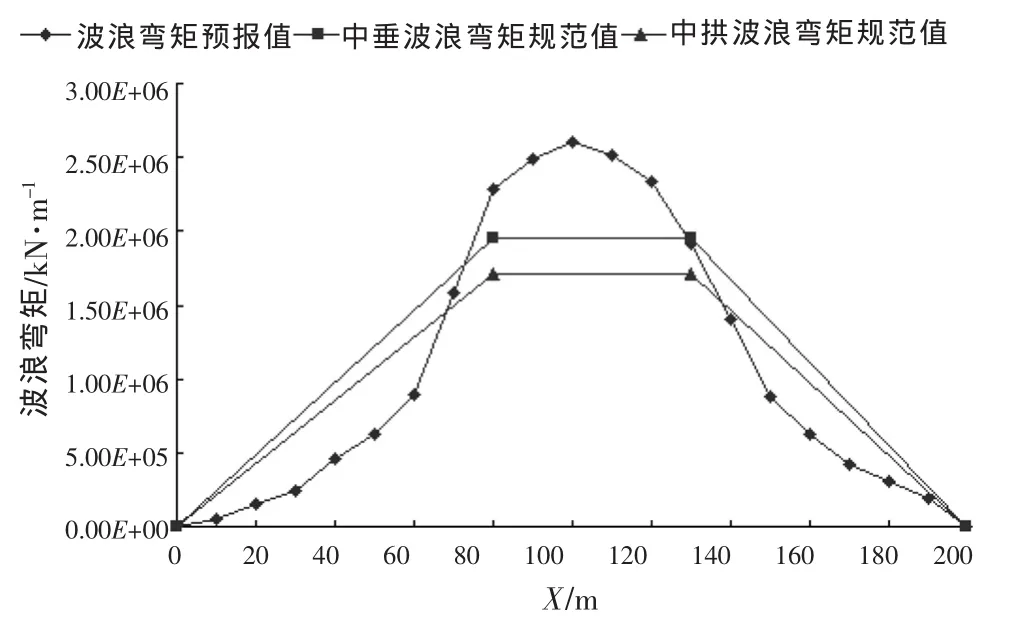
图4 B钻井船波浪弯矩预报值与规范值

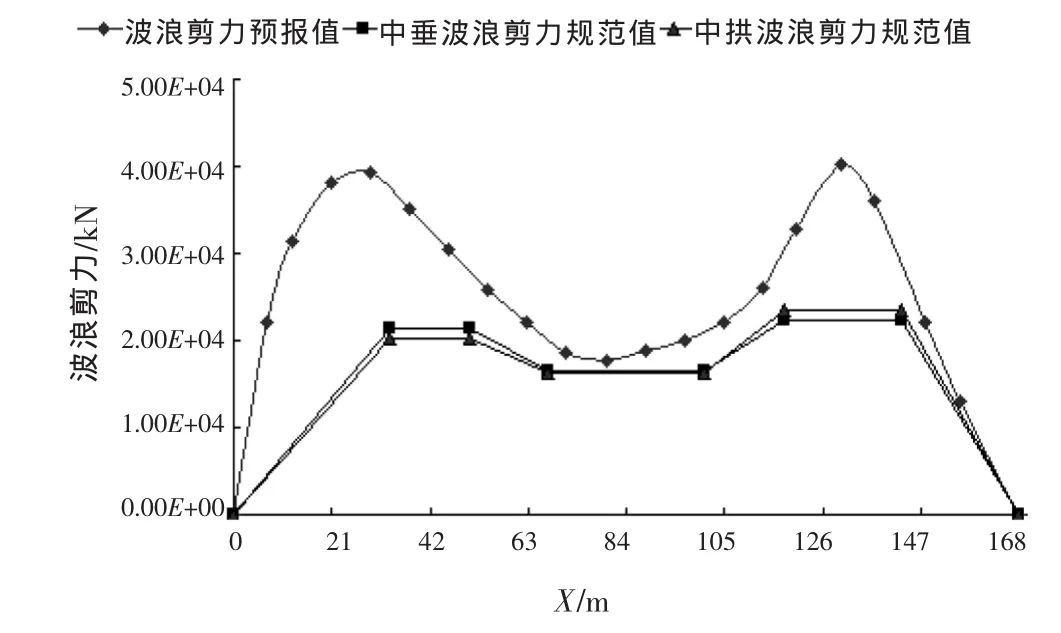
图5 A钻井船波浪剪力预报值与规范值

图6 B钻井船波浪剪力预报值与规范值

由图3~图6可以看出，两艘钻井船的直接预报最大值均大于规范计算最大值，其比较结果如表4所示。

表4 波浪载荷预报值与规范值比较

2.4 月池开口对波浪载荷的影响

除布置不同外，钻井船波浪载荷与常规船的区别还在于钻井船从甲板至船底的月池开孔。为了反映月池开孔对波浪载荷的影响，本文以A钻井船为母型，计算了其不考虑月池开口时的波浪载荷，并与原计算值比较。为方便区分，此处将不考虑月池开口的船定义为A1钻井船。不考虑月池开孔则会导致浮力增加、吃水减少。为保证波浪载荷计算比较的基础基本一致，计算中采用保持吃水不变，增加的浮力通过全船分布的质量点来平衡，并且保持重心位置不变。

影响结构设计的关键波浪载荷是波浪弯矩和波浪剪力，因此本节仅列出波浪弯矩和波浪剪力。A钻井船和A1钻井船的波浪载荷预报值比较见表5。

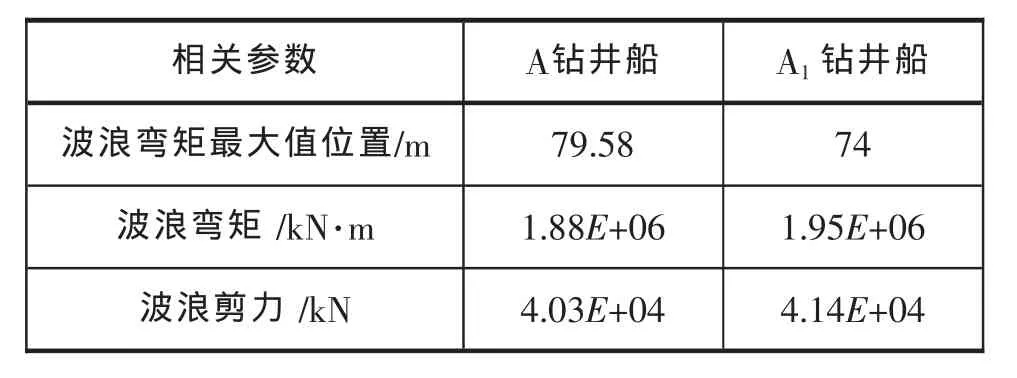
表5 月池开口对波浪载荷预报值影响比较

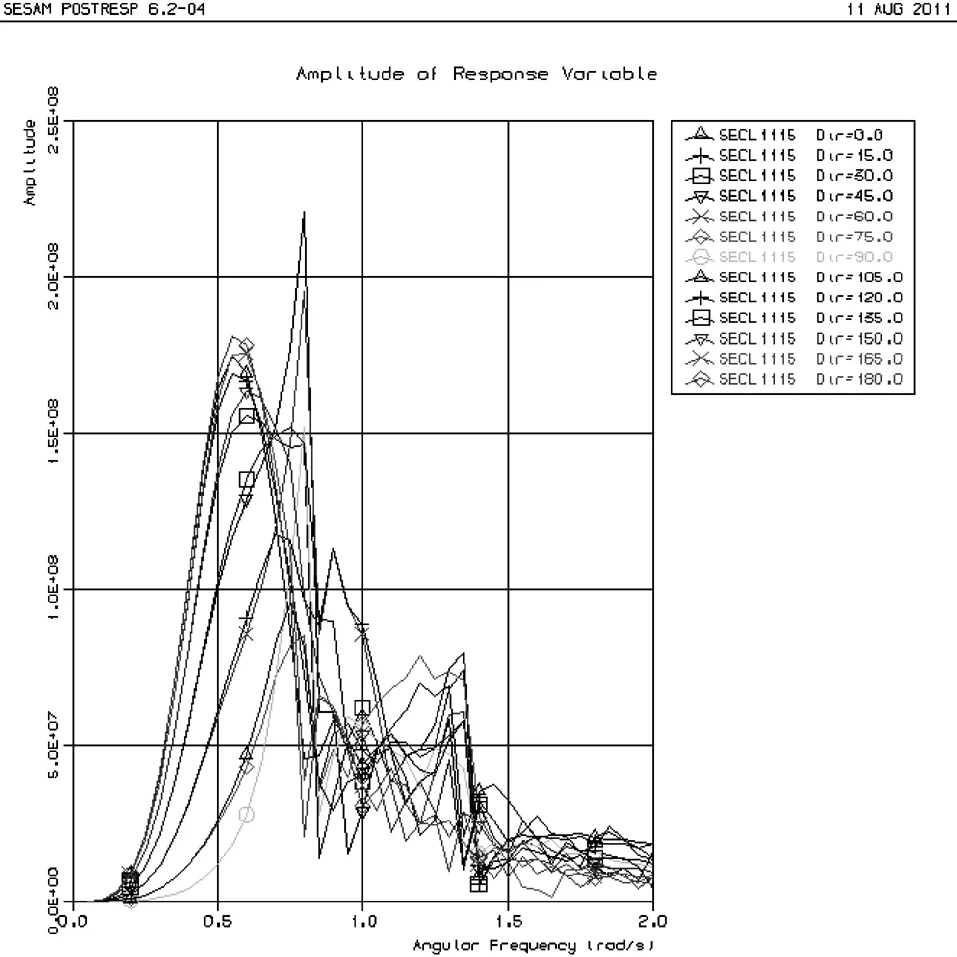
图7 A钻井船11号剖面处波浪弯矩传递函数

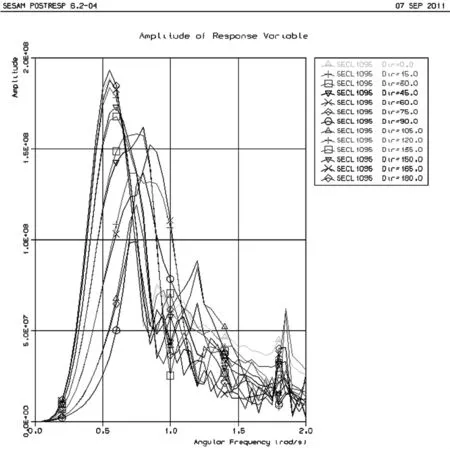
图8 A1钻井船9号剖面处波浪弯矩传递函数

波浪弯矩传递函数如图7和图8所示。

由表5可知，A1钻井船波浪弯矩的最大值位置相对A船向船尾方向移动了5.58m，A1钻井船波浪载荷预报值都比A钻井船大。由图7和图8可知，A钻井船RAO峰值出现的浪向角为45°，A1钻井船RAO峰值出现的浪向角为180°。

3 结论

波浪载荷作为总纵强度计算中的重要载荷，方案前期对其合理的预估是确定横剖面及钢料重量预估的关键。对于钻井船，由于其总体布置特殊，甲板设备众多，IACS推荐的规范计算公式不能很好反映其波浪载荷的分布。因此，本文试图从工程角度出发，通过对已有的两艘钻井船进行波浪载荷直接预报，并与规范计算值比较，可知预报值比规范值大。另外，通过对一条无月池开孔船波浪载荷的计算，可知不考虑月池开孔时，其RAO峰值出现的位置以及浪向角都与原钻井船不同。这些结论可以为结构工程师在钻井船前期设计时快速、有效反应提供一定的借鉴。

［1］张海彬，赵耕贤.水动力分析在海洋结构物设计中的应用［J］.中国海洋平台，2008（1）：1-6.

［2］吴小平.基于切片理论的波浪载荷直接计算［J］.上海造船，2010（4）：21-25.

［3］刘应中，缪国平.船舶在波浪上的运动理论［M］.上海：上海交通大学出版社，1987.

［4］戴仰山，沈进威，宋竞正.船舶波浪载荷［M］.北京：国防工业出版社，2007.

［5］DNV.WADAM-Wave Analysis by Diffraction and Morison Theory.SESAM User Manual［S］.Norway：Det Norske Veritas.2008.

［6］DNV.POSTRESP-Post process or for Statistical Response Calculations.SESAM User Manual［S］.Norway：Det Norske Veritas.2007.

［7］DNV.DNV Rules for Classification of Ship［S］.Norway：Det Norske Veritas.2003.

W ave loads prediction of deep water drilling ship

GUO Xing-qian
（Marine Design&Research Institute of China，Shanghai200011，China）

The transfer function of wave induced loads and the corresponding wave induced loads of two drilling ships are calculated in this paper.The prediction results are compared with the wave loads based on IACS requirements.Furthermore，the wave induced loads of one drilling ship without moon pool opening are calculated in order to find out the differences between drilling ships and general ships.It is helpful for drilling ship structural design.

drilling ship；wave loads；long term prediction

U661.4；U674.38+1

A

1001-9855（2012）03-0040-06

2011-09-15；

2011-10-17

郭兴乾（1987-），男，汉族，哈尔滨工程大学在读硕士，主要从事船舶结构分析工作。