有限元弹性动力分析与优化在某气门机构中的应用

孙先国，刘浩，倪计民

（1．同济大学汽车学院，上海200092；2．舍弗勒集团发动机部，上海201804）

有限元弹性动力分析与优化在某气门机构中的应用

孙先国1,2，刘浩2，倪计民1

（1．同济大学汽车学院，上海200092；2．舍弗勒集团发动机部，上海201804）

对某发动机气门机构建立了混合刚体-弹性体的参数化非线性有限元模型，进行了弹性动力学计算。通过回归方程对模型进行了优化，降低了摇臂的质量，在保证摇臂强度的同时改善了凸轮-滚子的接触性能，从而降低了磨损，提高了耐久性。

气门机构有限元法弹性动力回归优化

1 前言

以往的气门机构分析，多是将气门机构系统简化成单质量或多质量集总参数模型[1-5]，然后进行运动学和动力学分析。这种方法的优点是建模方便，计算快速，理论分析方便。另一种方法是将部件看成没有变形的刚体，并通过自由度耦合将各部件联接起来，组成一个多刚体系统[6-7]。通过矢量力学或分析力学，建立起规则统一的动力学方程组并求解。

随着气门机构向轻量化和高速化方向的发展[8-10]，部件柔度和惯性力的加大，部件的弹性变形可能给气门的运动输出结果带来误差，因此有必要计入这种变形对计算精度的影响[11]。计入变形的影响后，还能够在计算出动力学响应的同时得到部件的应力谱。

目前比较流行的包含弹性体多体系统的建模方法是相对坐标法。这种方法首先在弹性体上建立一个浮动坐标系，将弹性体的运动分解成浮动坐标系的牵连运动和其相对于浮动坐标系的变形运动的叠加。弹性变形则按无大范围运动时理想边界条件下的整体变形或模态函数进行离散，其中假设模态法在实际工程中得到了广泛的应用，成为很多商业动力学软件的理论基础[12-14]。假设模态法将整个弹性体的变形场表示为一组模态函数和模态坐标的线性组合。因为计算之前需要先进行模态分析，所以只能考虑小变形的情况，而且模态函数的选取有一定的随意性。

以Shabana[15]为代表的一派学者提倡将弹性体的大位移以及弹性变形都用相对总体坐标系的单元节点坐标描述，不区分物体的刚性运动和变形，对二者都按照连续介质力学的方式统一处理，在此基础上发展出能处理部件在任意范围内的大运动、大变形的非线性动力学模型，称之为绝对坐标法。相对坐标法可以看作是多刚体动力学框架内的推广。绝对坐标法实际上是一种有限元法，通过有限元网格离散的同时计算部件的刚体运动和变形（应力），而且可以直接计算弹性体之间的接触－冲击及滑动，这是假设模态法难以做到的。理论上非线性有限元的工具都有可能用来进行多体动力学分析。

有关用集总参数法或多刚体模型和假设模态法的刚－弹耦合模型的气门机构动力学计算例子已经有很多，但应用非线性有限元法对气门机构进行弹性动力分析尚少见相关的文献。

ABAQUS是一款基于非线性连续介质理论的通用非线性有限元软件，本文试图在ABAQUS软件的基础上，建立起适合计算气门机构的混合刚体－弹性体非线性有限元动力学模型。

2 模型处理

某发动机的气门机构模型如图1所示。有限元动力学模型的自由度比较多，如何正确反映模型的主要特点又尽可能地缩小模型的规模，是建模的首要考虑。比如刚度大的部件可以简化成刚体，有限元模型尽量使用壳单元和梁单元，避免使用实体单元等。

图1 总体几何模型

2.1 凸轮

凸轮结构的刚度比较大，为降低模型规模，凸轮简化成刚体，刚体的整体运动通过参考点控制（图2）。参考点即为坐标原点（0，0，0）。由于假设凸轮绕参考点作等速转动，不需要输入转动惯量。

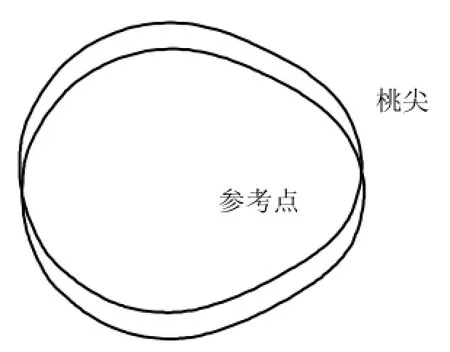
图2 凸轮刚体模型

2.2 滚子

滚子也即滚子轴承，整体刚度大，零件多，为了降低模型规模，滚子也简化成刚体（图3）。滚子的质量是16.8 g，对旋转轴的转动惯量是442 g·mm2。

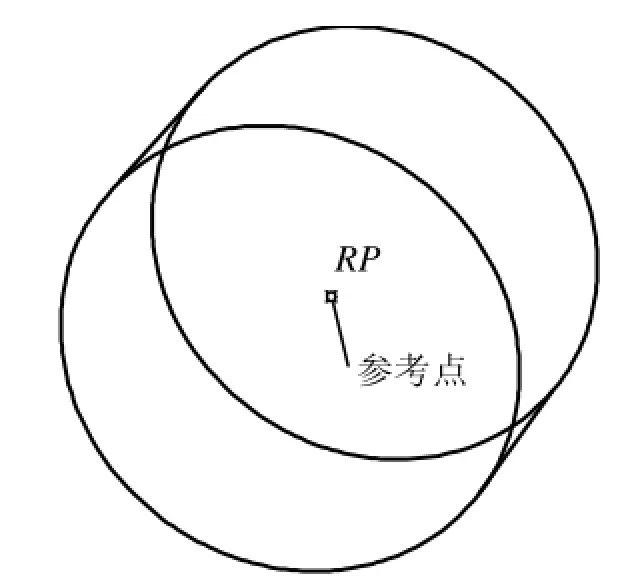
图3 滚子刚体模型

2.3 摇臂

摇臂是气门机构系统中承受凸轮和弹簧动载荷的部件，刚度不高，应使用弹性体模型（图4）。摇臂是钣金件，适合用壳单元模拟，并可以方便地通过定义壳厚h将摇臂模型参数化，摇臂壳厚为3 mm。

图4 摇臂有限元模型

摇臂使用通用缩减积分壳单元S4R，S4R单元可以根据定义的壳厚度自动选择薄壳或厚壳公式。限于篇幅，S4R通用壳单元的有限元格式本文不再详述，相关内容可以参考相关文献[16]。

2.4 气门与气门弹簧

气门虽然也有一定的变形，但本文气门不是关注的重点，仅取与摇臂接触的顶面做成刚体面，气门简化成参考点上的集中质量，如图5所示。

图5 气门与气门弹簧模型

除了气门外，弹簧上座、气门锁夹的质量也都集中到气门参考点上，三者质量之和为42.1 g。

弹簧对气门机构的动力学响应有重要影响[17-18]，等距螺旋弹簧刚度可计算如下[19]，式（1）中各项参数见表1。

式中，

K——弹簧刚度，N/mm；

G——气门弹簧剪切弹性模量，MPa；

d——钢丝直径，mm；

D——弹簧中径，mm；

n——有效圈数。

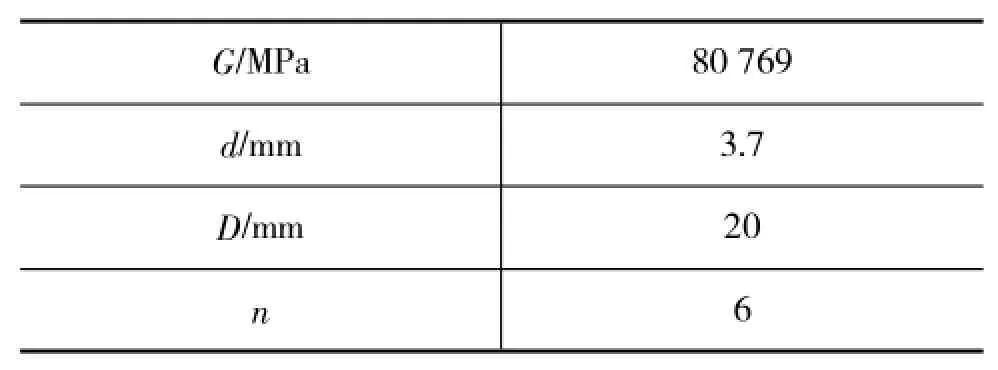
表1 弹簧参数

根据式（1）计算得弹簧刚度K=39.5 N/mm，与摇臂类似，可以通过定义d将弹簧模型参数化。

为了模拟弹簧的颤振效果，将弹簧分成11段，质量点之间以弹簧－阻尼联接，见图5。

每点的质量可以计算如下[20]：

其中，ρ为弹簧密度（同表2），其余同式（1）。

取1.85Mi的弹簧质量集中到气门参考点上（图5），其余质量点均取Mi。

文献[1]经试验研究建议，等距螺旋弹簧阻尼比δ取0.01～0.011。本文取0.011，弹簧阻尼可计算如下：

K、M、c分别为弹簧的总刚度、总质量和总阻尼。由于各个质量点是串联的关系，各质量点之间的弹簧阻尼要取总体刚度和阻尼的11倍。

3 模型设置

3.1 材料特性

气门机构各部件均由钢材组成。凸轮、滚子、弹簧、气门分别简化成刚体和集中质量，无需输入弹性材料参数。摇臂材料是16MnCr5，材料的特性参数见表2。

表2 摇臂材料参数

3.2 接触连接

凸轮－滚子（图1）、摇臂－气门（图5）之间的接触使用基于罚函数法的有限滑动、面－面接触公式[21]，摩擦系数为0.01。液压间隙调节器（HLA）不是关注的重点，可以简化成固定的接地点。摇臂右侧球面与接地点建立弹性连接（图6），耦合全部自由度。弹性连接将一组节点与一个参考点相连，由参考点控制被连接节点的几何运动。与刚性连接不同的是弹性连接允许被连接节点之间有相对位移，而且参考点所受载荷会根据被连接点的相对位置加权分配到各个节点上[21]。

图6 摇臂与接地点的连接

由于摇臂简化成壳单元，摇臂与滚子的接触面（图1）也退化成一圈节点（图7），两侧分别与位于圆心的参考点建立弹性连接，耦合全部自由度。

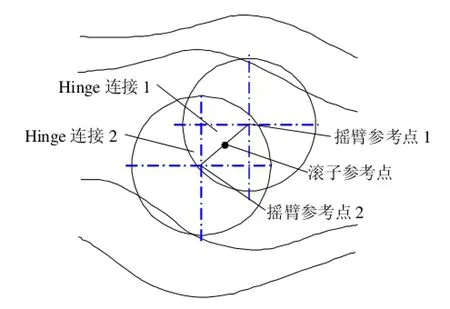
图7 摇臂与滚子的连接

ABAQUS的CONNECTOR单元提供了各种模拟2个点之间相对运动关系的方法；其中Hinge连接可以模拟2个点之间仅有一个自由度的相对转动[21]，符合滚子与摇臂之间的运动关系。

3.3 载荷工况

求解分以下几个步骤：

1）沿弹簧作用方向移动弹簧参考点（图5），使弹簧产生一个初始预紧力，同时凸轮－滚子、摇臂－气门建立接触关系。

2）转动凸轮参考点，带动凸轮以及滚子摇臂工作，假设凸轮轴转速是3 000 r/min（对应曲轴转速6 000 r/min）等速旋转。

3）凸轮工作时，固定凸轮参考点和摇臂接地点除转动方向的所有自由度，固定弹簧参考点。

4 模型计算

4.1 计算方法

考虑无阻尼结构动力学方程

式中，

M——质量矩阵；

K——为刚度矩阵；

F——是外力向量；

U——是位移向量。

方程（4）的初始条件

对t+Δt时刻，将方程（4）、（5）表示为如下形式

以上是HHT隐式积分格式[22]，其中β=1/4 (1-α2)，γ=1/2-α，-1/2≤α≤0。HHT法是Newmark法的推广，当α=0等同于Newmark法，二阶精度，无条件稳定。HHT法的优点是通过参数α自动在方程（4）中引入一个数值阻尼，并可以通过α方便地控制其大小。

由于网格离散形成的非光滑表面，有限元动力学模型在计算接触－冲击的时候会带来没有意义的高频响应。HHT法通过微小的数值阻尼就可以抑制高频噪声，而对低频的求解没什么影响，因此很适合用来求解有限元动力学问题。

4.2 气门的动态响应

取α=-0.414 21，每周计算360步，时间步长为5.5×10-5s。气门参考点的升程、速度、加速度曲线如图8所示，凸轮-滚子和气门-摇臂的接触力如图9所示。

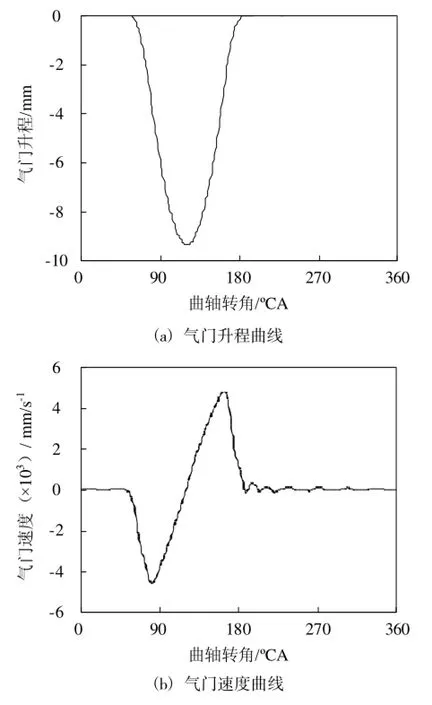
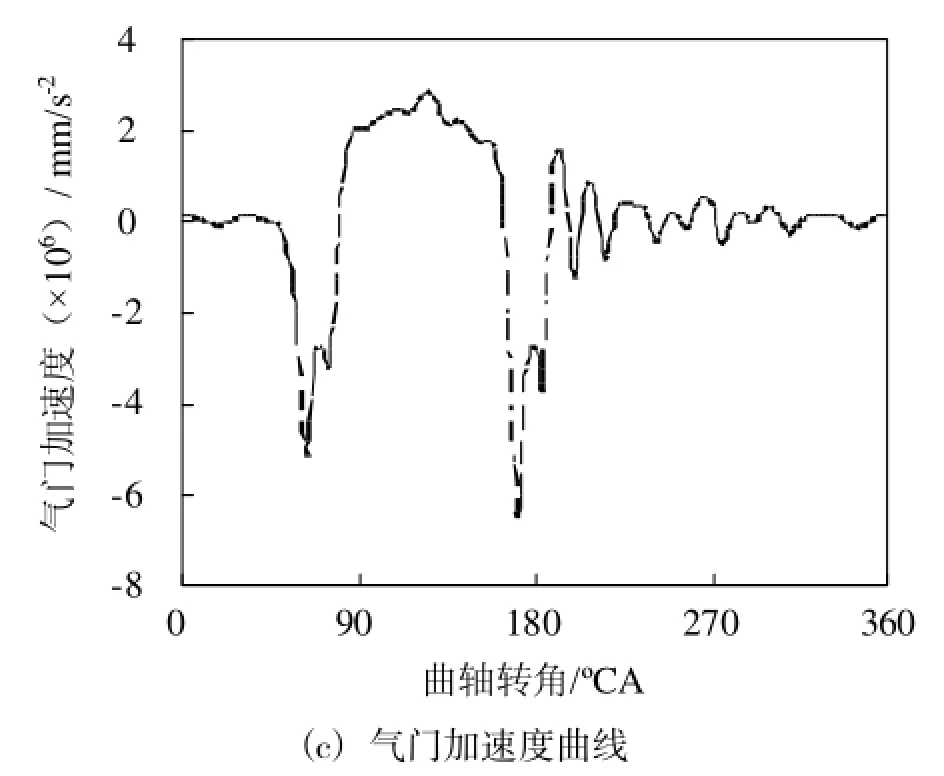
图8 气门响应特性

由图8可以看出，由于弹簧阻尼的作用，随着凸轮升程的结束，速度、加速度都会迅速衰减至稳定状态，符合实际的工作情形。由图9可以看出，接触力都有明显的波动效应，升程结束后迅速衰减。如果接触力小于0，气门和摇臂之间会出现飞脱，凸轮在旋转的同时气门升程却没有变化，气门不能正常工作，产生接触损失。本文中接触力在一个凸轮周期内都大于0。

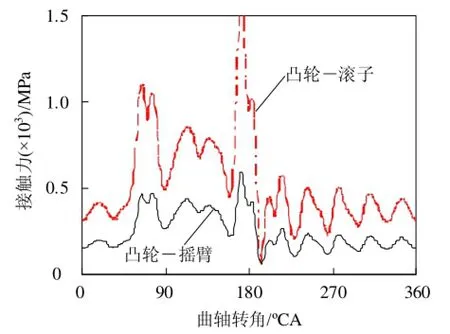
图9 凸轮－滚子和气门－摇臂的接触力

4.3 摇臂的强度计算

有限元弹性动力分析能在求解动力学积分的同时对包含单元的弹性体直接计算出每一步的应力，最大凸轮接触力时刻应力分布如图10所示。A是最大的应力集中点，在工作周期内A点的应力谱如图11所示。

可见A点应力谱和凸轮接触力非常相似，说明凸轮接触力是影响摇臂强度最重要的因素。厚为3 mm的摇臂模型A点应力最大值为103 MPa。

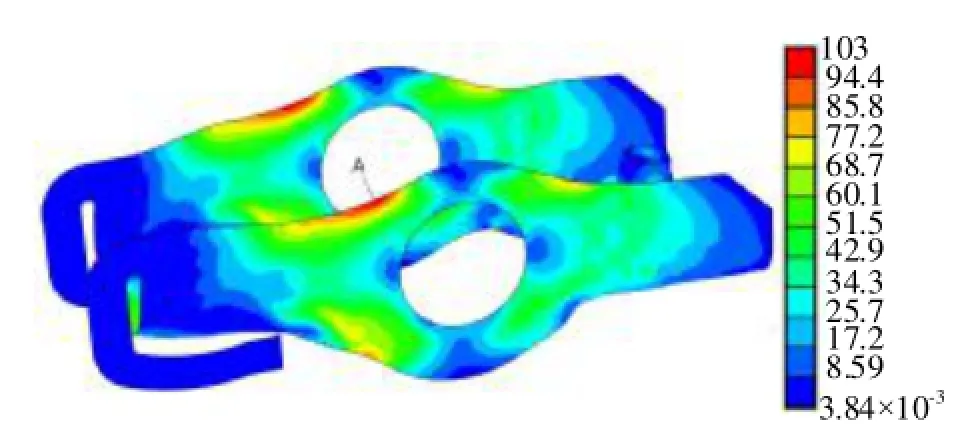
图10 摇臂应力分布

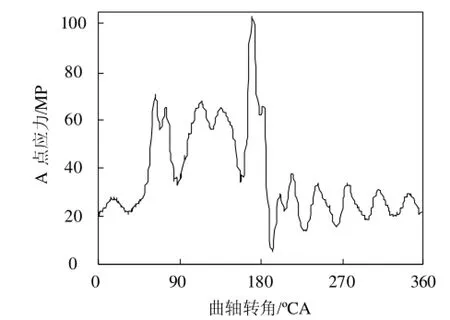
图11 A点应力谱

凸轮－滚子的接触应力Scon是气门机构性能最重要的评价指标之一。2个外圆柱之间的线接触可以按赫兹接触公式计算[23]。

式中：

F——接触力；

W——接触线宽度；

ρ1，ρ2——接触点处凸轮与滚子的曲率半径；

μ1，μ2——凸轮与滚子的泊松比；

E1，E2——凸轮与滚子的弹性模量。

表3中ρ1是最大接触力时刻凸轮的曲率半径，可以通过三点定圆法计算得到。凸轮－滚子最大接触力为1 514 N，根据式（9）相应的接触应力为921.9 MPa。

根据设计规范（表4），摇臂强度和接触应力满足要求，摇臂强度良好。但接触应力偏高，有必要对模型进行进一步优化。

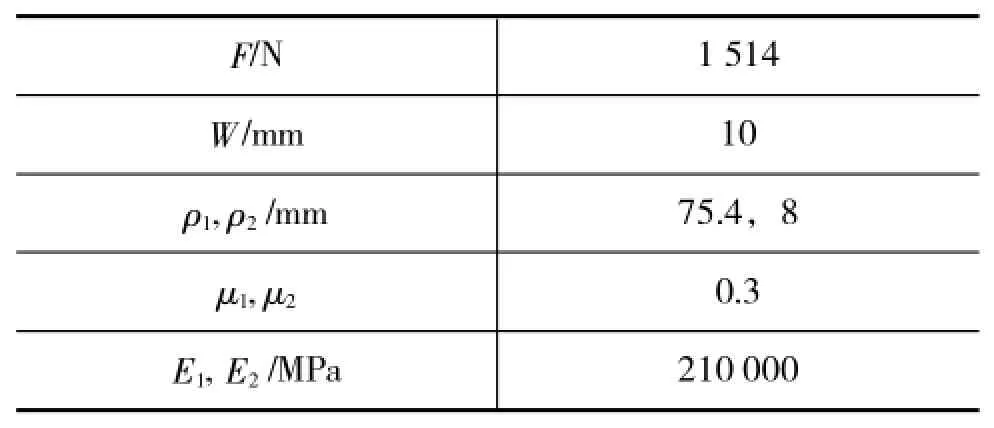
表3 接触输入参数

表4 设计规范（MPa）

5 模型优化

5.1 设计方案

使用壳单元摇臂模型和多点质量弹簧模型的优点之一就是可以方便地通过定义相关几何尺寸对模型参数化以便优化分析。选取摇臂厚度h和钢丝直径d作为设计变量，设计空间分别为h[2.1，3.0]和d[3.47，3.7]，厚度h取7个点，直径d取6个点，在二维空间上均匀布置，共42个方案，任一方案均是参数（h，d）的组合。

根据前述有限元模型和参数设计方案，摇臂A处最大应力和凸轮－滚子接触应力如表5和表6所示；摇臂A点应力和接触应力的响应面如图12所示。

表5 摇臂A点应力（MPa）

表6 接触应力（MPa）

图12 凸轮－滚子接触应力

从图表中可以看出无论是摇臂强度还是凸轮－滚子接触强度的响应面都接近平面，没有明显的凸面或凹面，并且单调。

5.2 回归优化分析

响应面法是基于回归理论的优化方法。根据一定数量的测试结果，建立输出参数和输入变量的经验方程，通过求解回归方程达到优化设计的目的[24]。多项式响应面模型是应用比较广泛的一种近似模型，通常使用二元二次模型[25]

实际应用中如果没有明显的凸面或凹面（图12），可以略去式（10）中的高阶项，简化为平面模型

使用Excel软件自带的多元线性回归工具分别对摇臂强度和接触强度结果进行回归分析[26]，得到摇臂强度Slever和接触强度Scon的回归方程

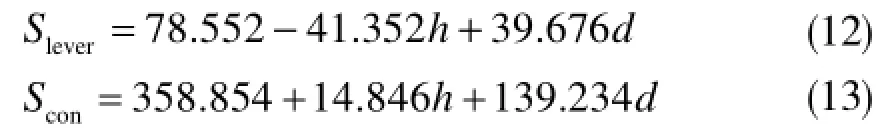
气门机构优化的目的是降低凸轮－滚子之间的接触强度使其进入“良好”区域，同时保证摇臂的强度在可接受区域内，也就是Slever≤125，Scon≤900。

将Slever=125，Scon=900代入式（12,13），可以得到摇臂厚度h=2.364，钢丝直径d=3.635。该计算结果只是由回归方程得到的理论值，考虑到摇臂实际的加工制造和弹簧元件选型的限制，取h为2.4 mm，d为3.6 mm，代入式（12,13），得Slever=122.1 MPa，Scon=895.7 MPa，符合设计要求。

将优化后的参数（2.4,3.6）重新代入模型，计算得到A点应力为119.8 MPa，凸轮－滚子接触应力为891.1 MPa，与前述回归方程计算结果的误差分别为1.88%和0.51%。凸轮－滚子接触力、气门加速度和摇臂－气门接触力对比如图13至图15所示。

图13 滚子接触力对比

图14 气门加速度

6 结论

针对某发动机气门机构建立了非线性参数化有限元模型，进行了隐式动力学分析，得到了摇臂和气门的强度及动力学响应，并对结果进行了优化分析。

图15 气门接触力

经回归优化设计后的气门机构摇臂厚度由3 mm降到2.4 mm，减重达20%；凸轮－滚子间的接触应力由921.9 MPa降到了891.1MPa，同时摇臂应力也满足设计规范。接触应力的降低有利于提高部件的疲劳耐久性和减少磨损。

由图13及式（12）和式（13）可以看到，摇臂强度和接触强度都是弹簧钢丝直径d的单调函数，d减少，摇臂强度和接触强度也都会降低。在前述优化结果的基础上，模型还有进一步优化的潜力，但前提是保证气门与摇臂的接触力大于0。

本例只是选取了摇臂在凸轮周期内的峰值应力校核摇臂强度。如果对摇臂应力谱用雨流计数法[27]之类的载荷统计工具，可以计算出摇臂在一个工作周期内所有的应力循环，结合疲劳分析理论得到更精确的强度寿命，这也是今后进一步开展工作的方向。

1尚汉冀．内燃机配气凸轮机构：设计与计算[M].上海：复旦大学出版社，1988．

2刘忠民，俞小莉，沈瑜铭．配气机构动力学模型的比较研究[J]．浙江大学学报，2005：39卷（12）．

3杨明轩.高速凸轮机构动力学模型研究[J]．机械，2007：（7）．

4 Husselman M．Modeling and Veriflication of Valve Train Dynamics in Engines[D]．Stellenbosch University，2005．

5 Desai H D，Patel V K．Computer Aided Kinematic and Dynamic Analysis of Cam and Follower[C]．London：Proceedings of the World Congress on Engineering，WCE 2010，2010：June 30-July 2．

6王晓，张保成．基于多体系统仿真的内燃机配气机构动力学分析[J]．内燃机，2008（1）．

7 Cofaru C，Sandu G，Jelenschi L，Multibodyanalysis of the finger follower valvetrain system[J]．Transilvania University of Brasov,2010．

8倪计民．内燃机原理[M]．上海：同济大学出版社，1997．

9张正有．发动机配气机构发展综述[N]．重庆工学院汽车学院，2002．

10路琼琼，李智，雷晶．内燃机配气机构技术现状及发展[J]．机械，2009年，36（4）．

11张策．机械动力学[M]．北京：高等教育出版社，2000．

12赫永刚．基于多体系统的配气机构动力学特性研究[D].浙江大学机械与能源工程学院，2006．

13杨辉．刚－柔耦合动力学系统的建模理论与实验研究[D]．上海交通大学，2002．

14 Dalpiaz G，Rivola A．A model for the elasto-dynamic analysis of a desmodromic valve train,tenth world congress on the therory of machines and mechanics[J]．Finland：Oulu,1999：June 20-24．

15 Shabana A A.Computational continuummechanics[M]. Cambridge University Press，2008．

16 Abaqus Theory Manual.Dassault Système,2011．

17傅红良，林运．气门弹簧特性对配气机构的影响[J]．柴油机设计与制造，2007（3）.

18徐小明，蒋炎坤，刘志恩．基于分离变量法的发动机配气机构弹簧动力学模拟[J]．柴油机，2007：（29）4．

19季文美等．机械振动[M]．北京：科学出版社，1985．

20 Seidlitz S．Valve train dynamics-A computer study[C]．SAE 890620．

21 Abaqus Analysis Manual.Dassault Système,2011．

22 Hilber H M，Hughes T J R，Taylor R L．Improved Numerical Dissipation for Time Integration Algorithms in Structural Dynamics[J]．Earthquake engineering and structural dynamics，Vol.5,283-292,1977．

23Johnson K L著．接触力学[M]，徐秉业等译．北京：高等教育出版社，1992．

24贵劲松，康海贵．结构可靠度分析的响应面法及其MATLAB实现[J]．计算力学学报，2004，21（6）．

25付凌晖，王惠文．多项式回归的建模方法比较研究[J]．数理统计与管理，2004，23（1）．

26艾自胜等．Excel在曲线拟合中的应用[J]．苏州大学学报（医学版），2008，28（5）．

27徐灏．疲劳强度[M]．北京：高等教育出版社，1988．

The Application of FEM Elastic-dynamic Analysis and Optimization in a Valve Train

Sun Xianguo1,2,Liu Hao2,Ni Jimin1
（1 Automobile Academy,Tongji University;2 Engine Dept.,Schaeffler Group,China）

An elastic-dynamic analysis of a valve train is carried with parametric nonlinear rigid-flexible FEM mode,and then the mode is optimized by regression equation.As a result,the mass of the lever is reduced,and the contact performance between cam and roller is improved when the strength of the lever is safe at the same time,so the fatigue durability is improved and the wear of cam and roller decreased.

valve train,FEM,elastic-dynamic,regression optimization

10.3969/j.issn.1671-0614.2012.04.002

来稿日期：2012-08-07

孙先国（1981-），男，高级工程师，主要研究方向为机械结构有限元分析。