惯导系统传递对准技术研究及海试验证

齐广峰，王悦阳

（1.海军装备部，西安 710043；2.中航工业西安飞行自动控制研究所，西安 710065）

传递对准是指在载体航行过程中，以载体上已经工作在导航状态的高精度惯导系统(简称主惯导)的导航信息为基准，实现对载体上需要对准的导航系统(简称子惯导)的初始对准[1-2]。具体做法是，刚进入传递对准时，子惯导以当前时刻收到的主惯导位置、速度、姿态为初始导航参数，开始进行导航计算。而实际上子惯导的真实姿态、航向与主惯导的姿态、航向并不完全相同，存在安装误差，因而直接用主惯导的姿态、航向作为子惯导的初始姿态、航向会造成子惯导的初始数学平台偏角，从而造成子惯导的导航误差[3]。通过准确建立子惯导的导航误差数学模型，在传递对准过程中，以主惯导的导航信息为基准，通过卡尔曼滤波计算估计出子惯导的导航参数误差及陀螺漂移、加速度计零位等元件误差并加以修正[4-5]，实现子惯导的运动中对准。

在传递对准过程中，为了增加系统误差的可观测性，确保传递对准精度，通常要求对载体作机动运动，如要求载体作加速运动或作S型运动[6]等。但是由于试验船无法实现要求的机动运动，因而对于惯导系统传递对准而言，要在规定的对准时间内满足对准精度要求，对系统传递对准方案提出了更高的要求。

针对上述问题，我们设计了一种传递对准方案，该传递对准技术具备如下的优点：①在传递对准过程中，不专门要求载体作机动运动，就可在运动过程中完成传递对准计算；②在较短的对准时间内达到较高的传递对准精度；③能有效抑制扰动运动对传递对准精度的影响。

系统在试验船上完成了数十次的传递对准试验。达到的对准指标是：传递对准时间7 min，水平对准精度3"，方位对准精度3.3'。

1 系统方案设计

1.1 坐标系选择

1)载体坐标系(O−XYZ)。

载体坐标系为：选择惯性敏感元件(陀螺、加速度计)敏感轴交点为坐标原点O，X轴指向载体左翼，Y轴指向载体、纵轴，Z与X、Y 成右手系。

2)导航坐标系。

选择导航坐标系为东(E)、北(N)、天(U)坐标系。

1.2 系统状态方程和量测方程

1.2.1系统状态方程

选取到达状态变量X为[7-8]：

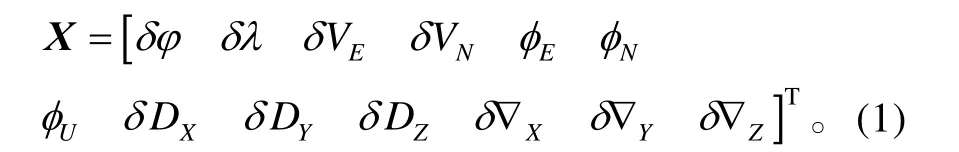
式(1)中：δϕ、δλ分别为纬度误差、经度误差；δVE、δVN分别为东向速度误差、北向速度误差；φE、φN、φU分别为数学平台东向、北向、天向偏角；δDX、δDY、δ DZ分别为X、Y、Z 向陀螺漂移；δ∇X、δ ∇Y、δ∇Z分别为X、Y、Z 向加速度计零位。

系统状态方程为：

式(2)中：W是系统噪声，为零均值高斯白噪声；

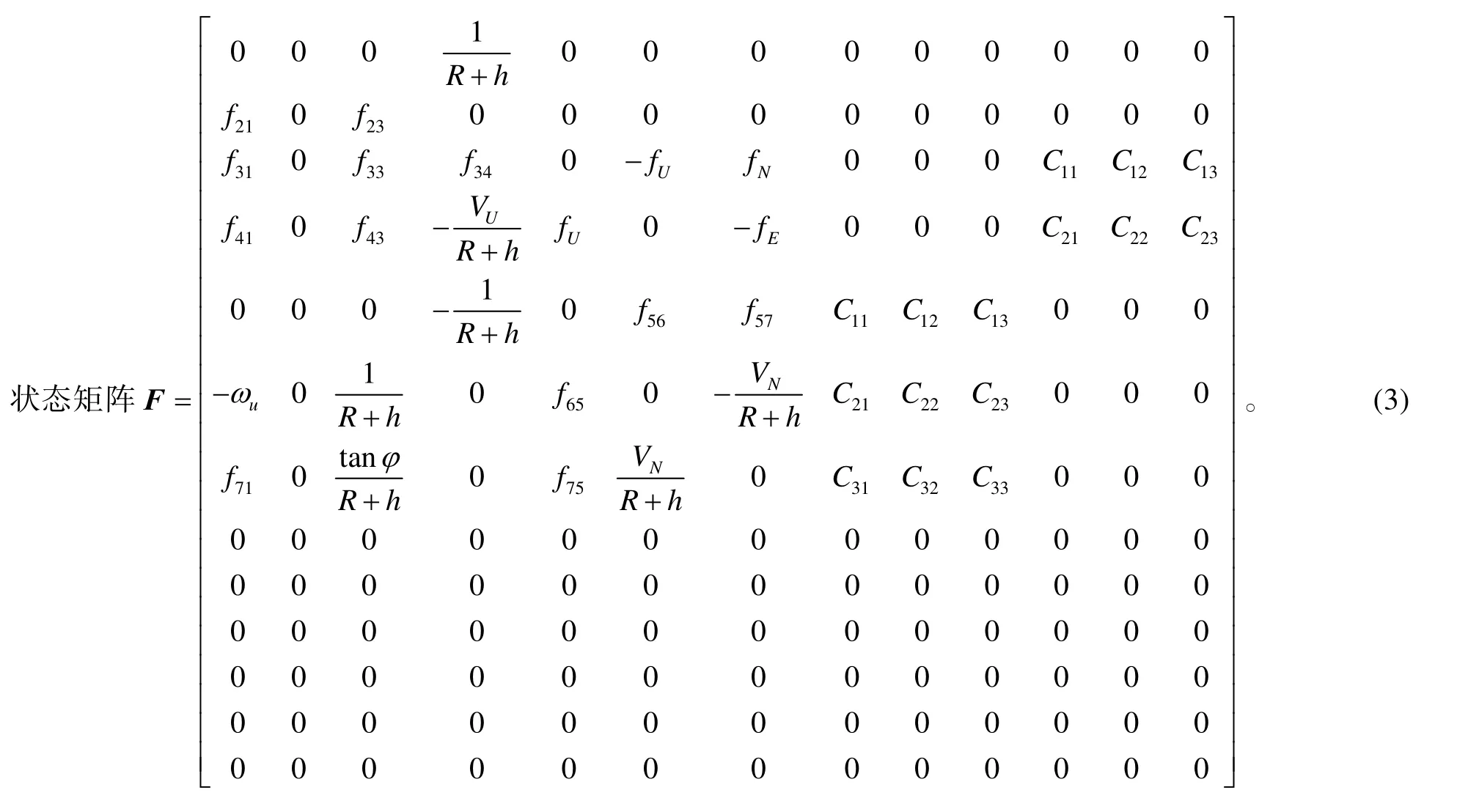
式(3)中：R是地球半径；h是载体高程；

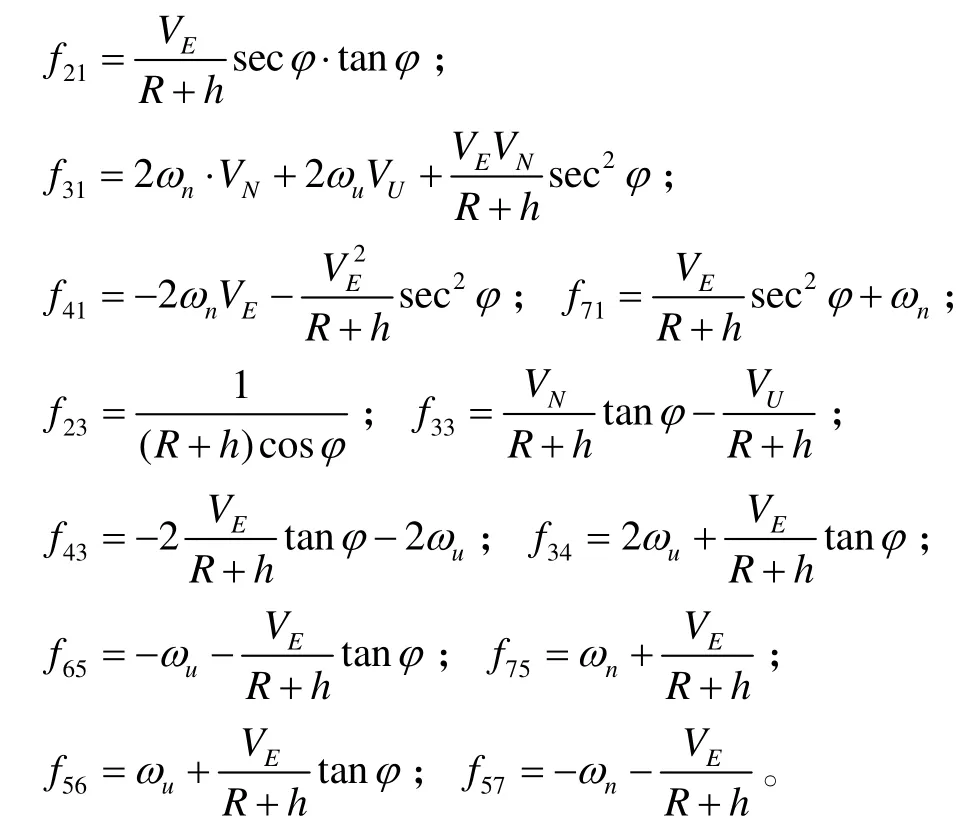
1.2.2系统量测方程

选取位置、速度作为卡尔曼滤波器[9]量测变量，量测方程如下：

式(4)中：V是量测噪声，为零均值高斯白噪声。

量测矩阵H为：

1.3 传递对准计算框图

传递对准计算框图如图1所示。

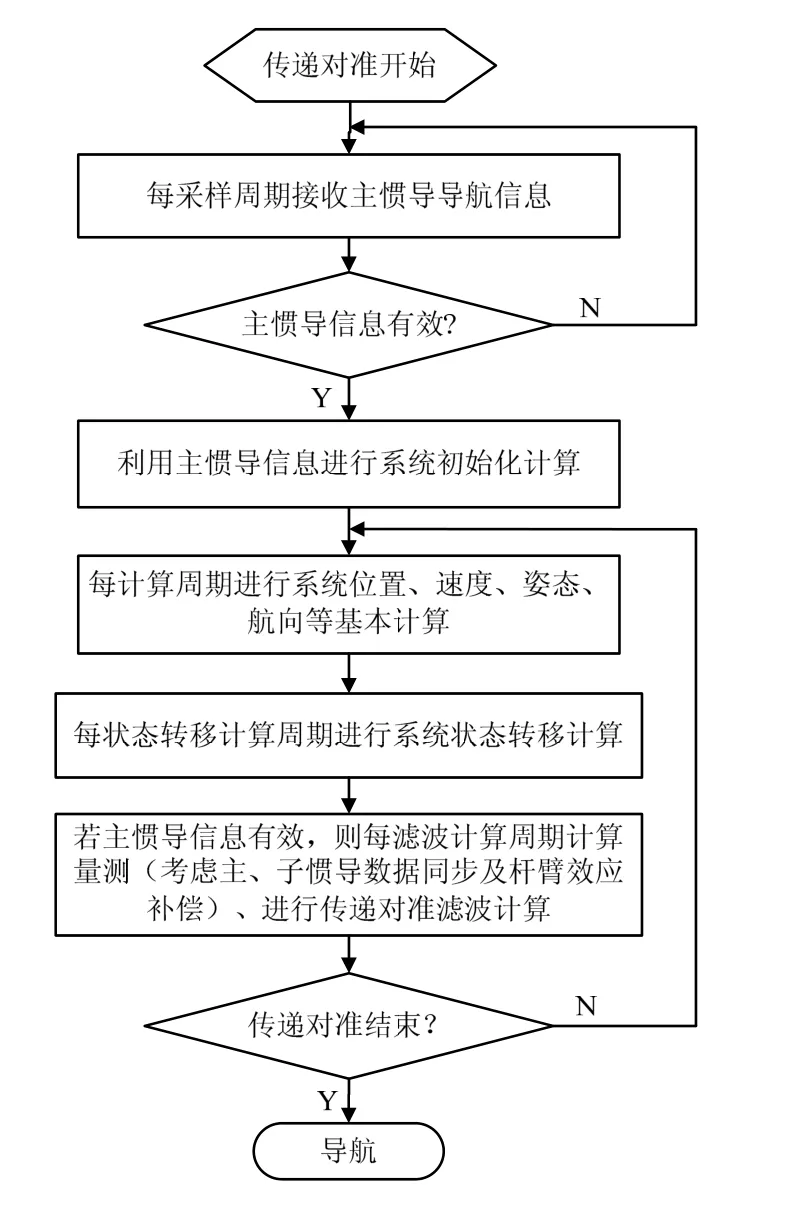
图1 传递对准计算框图

2 传递对准仿真计算

2.1 仿真计算条件

在仿真计算中，取平台东向、北向、天向初始偏角分别为3°、3°、7°。

2.2 仿真计算结果

按照2.1的仿真计算条件进行传递对准仿真计算，得到传递对准的第1、2、3、4、5、6、7 min时刻平台东向、北向、天向偏角估计误差，见表1。传递对准7 min 内平台东向、北向、天向偏角估计误差变化过程见图2a)～c)。

表1 传递对准过程中平台偏角估计误差

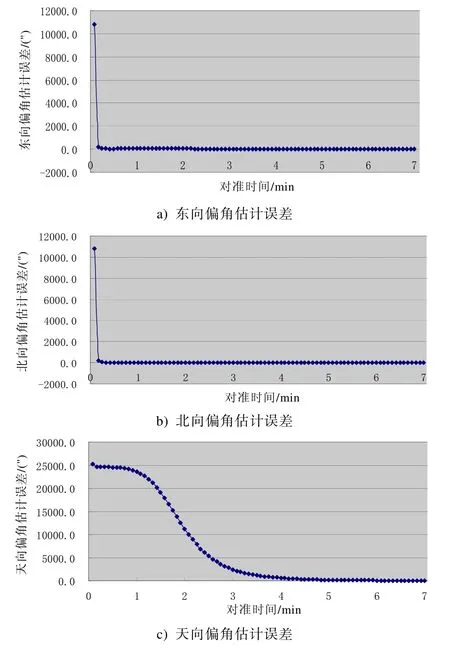
图2 传递对准7 min 内平台偏角估计误差

3 传递对准海试验证

海上试验时，参试的主惯导、子惯导及试验设备在试验船的同舱室安装，主惯导安装在基座上，子惯导安装在基座附近的舱室地板上。

3.1 试验方法

在试验船运动过程中，利用主惯导提供的导航信息为参考[10]，对子惯导进行运动中传递对准。传递对准7 min后，子惯导转入纯惯性导航状态。

在纯惯性导航过程中，分别以主惯导和卫星导航系统的导航信息为基准，对子惯导系统的传递对准精度进行评估[1，11]，得到各次传递对准的精度。

3.2 试验结果

3.2.1 传递对准精度

各次传递对准结束后，分别以主惯导及GPS为基准，计算惯导系统的导航误差，根据惯导系统的导航误差估计，得到传递精度，分别见表2、3，表中对准时间均为7 min。

表2 以主惯导为评估基准得到的传递对准精度

表3 以卫星为评估基准得到的传递对准

根据表2、3 统计计算得到对准时间为7 min时传递对准精度如下。

1)与主惯导比较。

东向数学平台偏角精度(RMS)为3.16"；北向数学平台偏角精度(RMS)为1.86"；方位数学平台偏角精度(RMS)为0.035º；与主惯导的航向差(RMS)为0.065º。

2)与GPS 比较。

东向数学平台偏角精度(RMS)为7.13"；北向数学平台偏角精度(RMS)为6.89"；方位数学平台偏角精度(RMS)为0.050º；与主惯导的航向差(RMS)为0.065º。

3.3.2 纯惯性导航精度

分别以主惯导、卫星导航系统为基准，计算子惯导完成7 min 传递对准后，在纯惯性导航状态的位置、速度精度，见表4、5。与GPS相比较计算位置误差[1]时，扣除了由于主惯导位置误差而造成的子惯导初始位置误差。

表4 以主惯导为评估基准得到的纯惯性导航精度

表5 以卫星导航系统为评估基准得到的纯惯性导航精度

根据表4、5，统计得到导航精度如下。

1)与GPS 比较的导航精度。

a) 1 h 导航精度时：位置误差CEP为0.69 n mile/h；东向速度误差RMS为0.43 m/s；北向速度误差RMS为0.44 m/s。

b) 1.5 h 导航精度时：位置误差CEP为0.70 n mile/h；东向速度误差RMS为0.38 m/s；北向速度误差RMS为0.41 m/s。

2)与主惯导相比较的导航精度。

a) 1 h 导航精度时：位置误差CEP为0.50 n mile/h；东向速度误差RMS为0.32 m/s；北向速度误差RMS为0.33 m/s。

b) 1.5 h 导航精度时：位置误差CEP为0.53 n mile/h；东向速度误差RMS为0.29 m/s；北向速度误差RMS为0.30 m/s。

4 结论

在实际使用中，子惯导载体的航向相对于主惯导的航向偏差可精确测量得到，因而可以将子惯导传递对准的初始航向误差控制在几度范围内。因此，本文设计的激光捷联惯导系统传递对准方案在传递对准过程中不需要对试验船提任何机动运动要求。仿真分析和海上试验结果均表明：论文设计的方案达到了较高的传递对准精度及纯惯性导航精度，为系统今后实际使用奠定了良好的基础。

[1]张宗麟.惯性导航与组合导航[M].北京:航空工业出版社,2000:197-198;241-243.

[2]秦永元.惯性导航[M].北京:科学出版社,2006:211-212.

[3]刘毅,刘志俭.捷联惯性导航系统传递对准技术研究现状及发展趋势[J].航天控制,2004,22(5):50-55.

[4]徐仕会,冯培德,雷宏杰.惯性导航系统扰动基座对准仿真研究[J].计算机仿真,2008,25(11):88-90.

[5]顾冬晴,秦永元.船用捷联惯导系统运动中对准的UKF 设计[J].系统工程与电子技术,2006,28(8):1218-1220.

[6]黄昆,杨功流,刘玉峰.舰载姿态加角速度匹配传递对准方法研究[J].中国惯性技术学报,2006,12(1):17-21.

[7]戴洪德,陈明,周绍磊,等.一种新的快速传递对准方法及其可观测度分析[J].宇航学报,2009,30(4):1449-1454.

[8]谭红力,黄新生,岳冬雪.捷联惯导大失准角误差模型在快速传递对准中的应用[J].国防科技大学学报,2008,30(6):19-24.

[9]HAO Y,XIONG Z,WANG W,et al.Rapid Transfer alignment based on unscented kalman filter[C]//Proceedings of the 2006 American Control Conference.2006:2215-2220.

[10]樊荣.捷联惯性导航系统初始对准方法研究及其仿真[D].南京:南京理工大学,2006.

[11]戴洪德.舰载机捷联惯导系统动基座对准技术研究[D].西安:西北工业大学,2008.