任意拓扑结构的耦合振荡器阵列及其在共形阵中的应用

凌 祥，胡志慧，姜志森

（1.海军航空工程学院电子信息工程系，山东 烟台 264001；2.海军装备研究院，上海 200436）

随着微波集成电路技术的发展，有源集成天线成为近年来一个很重要的研究领域。有源集成天线将有源器件和天线单元集成起来，使得其既具有传统辐射单元的功能，同时又具备了信号和波形处理能力，如混频、放大[1]。1993年，R.A.York首先提出了基于有源集成天线阵列的波束扫描新方法[2]，这种新的相控阵天线不需要移相器，具有低成本、小型化、易集成的优点，特别是在毫米波段，由于无须高性能的移相器，使得该技术更具优势。图1是他提出的一维线阵的原理图，相邻振荡器通过耦合线进行互相耦合，通过对称地控制阵列边界单元的自由振荡频率，可以在阵列中实现线性的相位分布，用于无移相器的波束扫描。这种阵列利用振荡器之间的耦合来实现波束扫描，因而也被称为耦合振荡器阵列。

York和随后的众多学者对一维和二维平面阵列的理论进行了深入研究[3-6]，并设计了实验阵列对原理进行验证。Ted Heath等人还设计了25单元的二维耦合振荡器阵列天线用于L1波段的GPS中[7]。

机载、弹载和星载相控阵天线由于飞行器的限制，更适合采用共形阵列天线，将天线单元安装在飞行器的表面上，使阵列天线表面与飞行器表面相吻合，既可以克服波束扫描范围窄，天线增益和测角精度随扫描角的增加而降低的缺陷，同时还可以改善飞行器的空气动力学性能。而耦合振荡器阵列天线体积小、集成度高、并且不需使用移相器，因此在共形相控阵中具有较好的应用前景。

图1 一维耦合振荡器阵列天线原理图

到目前为止，York等学者研究的耦合振荡器阵列都是平面模型，而共形相控阵的单元都是分布在曲面上的，曲面耦合振荡器阵列的波束扫描方法与平面阵列差别很大，必须建立曲面耦合振荡器阵列模型，找到曲面阵列相位控制的新方法，这样才有可能实现共形阵列。

本文提出了一种任意拓扑结构的曲面耦合振荡器阵列模型，讨论了幅度方程对阵列稳态性能的影响。采用图论的方法讨论了当自由振荡频率任意分布的情况下，相位方程定点唯一存在性的条件，并分析了其稳定性和单元间相位差的范围。最后，对圆柱形阵列天线进行了仿真，表明本文提出的任意拓扑结构的曲面耦合振荡器阵列有可能用于波束扫描，并且可以看到York等人的平面耦合振荡器阵列波束扫描方法是本文方法的一个特例。

1 任意拓扑结构的曲面耦合振荡器阵列

共形阵列天线波束扫描时，当天线波束最大值在(θ0,φ0)方向上时，每个天线单元的相位加权Δ φi0必须为[8]：

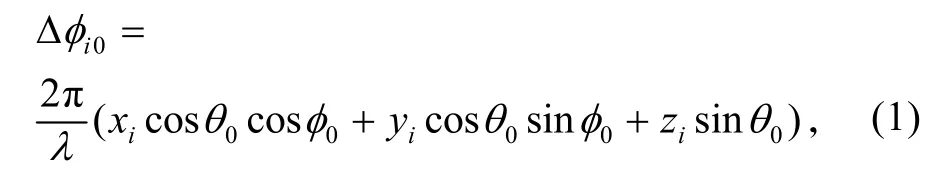
式中，(xi,yi,zi)为第i个单元在空间中的坐标。由于每个单元的相位加权不是线性分布的，平面耦合振荡器阵列模型难以用于共形阵列，因而首先建立任意拓扑结构的曲面耦合振荡器阵列模型，见图2。M为一曲面，圆点代表了振荡器，虚线代表耦合线。

图2 具有任意拓扑形式的曲面耦合振荡器阵列

对利用任意N 端口互耦网络连接N个正弦振荡器组成的阵列(如图1或图2)的分析方法是相同的，都可分2步进行：首先，用Y 参数来表达和分析耦合网络；然后，对振荡器进行建模，进而得到各振荡器振荡幅度及相位满足的一般微分方程组。平面阵列的幅度和相位方程推导过程在文献[2]中作了详细介绍，这里直接给出结论：

式(2)中：i=1,2,…,N；Ai是振荡器瞬时幅度；αi是自由振荡幅度；ωi为自由振荡频率；ϕi为振荡器的瞬时相位；μ是描述振荡器增益的经验值；Q为振荡器品质因素；Φij和εij分别为振荡器单元之间的耦合相位和耦合系数，当εij=0振荡器之间不耦合，每个振荡器处于自由振荡器状态，振荡幅度为Ai=αi，频率为ωi。

对任意耦合形式的阵列而言，它的相邻耦合单元不定，将其中第i个振荡器的所有相邻单元的序号组成一个集合，并记为Si。为简单起见，假设耦合相位 Φij=0。对第i个振荡器而言，定义来自第j个振荡器的耦合强度 ρi=εijAj，该参数影响阵列能否同步。在分析时可设定一个常数作为每个振荡器共同的耦合强度，这样既降低了对方程分析的难度，同时在阵列设计时也是可以实现的。改写方程(2)可得任意耦合形式的振荡器阵列幅度、相位方程

由于我们对相位方程更为关心，希望能够在一定条件下对幅度方程进行近似简化。因此，首先来定性地分析幅度方程对阵列稳态的影响。

将幅度和相位组成复数Ei=Aiejϕi，同时引入一个复数参数Ec，定义如下：

Ec可以被看作是阵列状态参数，用来考察阵列的幅度和相位是否实现了同步[9]，图3中的星号代表复数Ec。假设有N=16的振荡器阵列，其自由振荡频率 ωi在锁相带宽内随机分布，品质因素Q=10，令ρ=0.1。

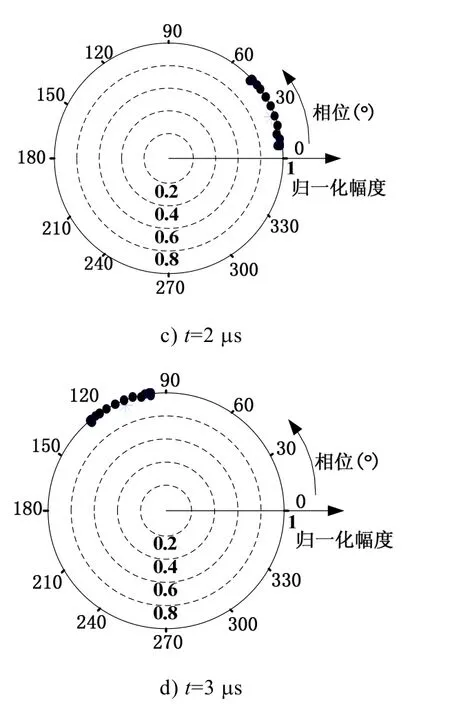
图3 增大耦合强度后的阵列相位幅度分布变化图

从图3中可以发现，每个振荡器的幅度很快达到一致，但虚线圆的半径稍大于振荡器自由振荡幅度iα，这是由于振荡器之间的耦合强度增大所造成的。从c)、d)两张图看到振荡器之间的相位也被锁定了，因为这两张图只是旋转了一个角度。也可以从 Ec的分布来考虑，图中的星号总是沿着虚线圆运动，说明 Ec也达到了稳定状态。

振荡器阵列的幅度通常比相位更早达到稳定，即使在相位失锁状态下，较小的耦合强度也能使幅度都达到一致。因此，在实际电路中，如果能保证振荡器单元尽可能一致，那么在阵列相位锁定状态下，可以忽略幅度对阵列状态的影响。为了使阵列达到相位锁定状态，ρ 必须大于某一值ρlock，ρlock的确定将在下面讨论。

由于振荡器输出信号带宽远小于其中心频率，即ωi的变化范围较小。因此，可以改写(3)中的相位方程，得到

2 相位方程稳定性分析

利用图论方法对耦合振荡器阵列定点稳定性进行分析，可以把耦合振荡器阵列看成是一个图G，阵列中的振荡器单元是图中的顶点V，而振荡器之间的耦合线可以看成是图的边E。假设有N个振荡器，M条耦合线，即图含有N个顶点、M条边。图可以用矩阵来表示[10]，图的邻接矩阵 A=(aij)，是一个N×N矩阵，其定义为

邻接矩阵表明了图中哪些顶点之间有边存在，是相邻的。另一个重要的矩阵是关联矩阵 B=(bij)，是一个N×M矩阵，其定义为

利用矩阵来改写耦合振荡器的相位方程(5)，ϕ和ω分别为N×1的阵列相位向量和自由振荡器频率向量，

当方程(6)处于稳态时，

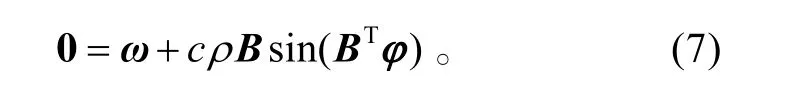
首先要判定的是该稳态方程是否有解，再来分析解的稳定性如何。利用Banach 不动点原理可以证明[11]，当耦合强度满足式(8)时，方程(7)存在唯一的解且振荡器之间的相位差范围为

式(8)中：λ2(BBT)和λN(BBT)分别为BBT的最小非零特征值和最大特征值，为范数。

式(8)给出了阵列相位锁定时，耦合强度ρ 必须达到的最小值ρlock。

式中，C为N×N的系数矩阵(雅可比矩阵)，

根据方程(6)，可以得到雅可比矩阵C，

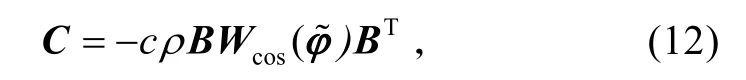
在分析定点的唯一存在性时，已知稳态时相邻单元之间的相位差的取值范围为那么，向量中的任一元素都大于0。根据图论中的定理[10-11]，TBB是一个半正定的对称阵，由此得知矩阵C的特征值均为负(含一个0 特征值)。根据线性稳定性定理，对应的微小扰动δ 将以指数形式快速地衰减，阵列的稳态相位分布ϕ～是线性稳定的。

3 数值仿真

圆柱形相控阵是目前研究得较多的一种共形相控阵，仿真时我们采用如图4a)所示的圆柱形拓扑结构的5×5耦合振荡器阵列，耦合方式采用最邻近耦合法，每个振荡器都接有一个辐射单元，并且振荡器的自由振荡频率分别可控。圆柱面的圆心角α=60°，阵列中俯仰面单元中心间距 dy=0.5λ0，水平面单元中心沿圆柱表面间距 dx=0.5λ0。

图4 5×5的圆柱形耦合振荡器阵列

假设主瓣位于俯仰方向θ=20°，水平方向φ=50°(主瓣水平方向扫描的中心位置在φ=30°)时，仿真步骤如下：

1)首先按照式(1)计算出每个振荡器单元需满足的相位分布 ϕs(单位为角度)，

式中，ϕs就是稳态时阵列所要求的相位分布，其水平单元(每一行内)相位差是不同的，而俯仰单元(每一列内的)的相位差是恒定的，这是由于俯仰方向上的振荡器分布在直线上。

2)根据式(7)，并假设cρ=1，可计算得到自由振荡器频率的分布ωs(为相对频率，围绕着0分布，已减去平均值)。

式中，ωs的均值为0，这说明阵列在进行波束扫描时，工作频率不变。阵列俯仰方向上边界单元的自由振荡频率呈反对称分布，这与York 等人提出的平面耦合振荡器阵列波束扫描方法是一致的，说明平面阵列的波束扫描方法是本文曲面阵列相位控制方法的一个特例。

3)将阵列中的自由振荡频率按ωs分布，对相位动力学方程组(4)进行仿真，图5只列出了第一行和第一列单元的相位随时间演变图，可以看到稳态相位与ϕs完全一致。

图5 阵列第1行和第1列单元相位随时间演变图

图6为仿真得到的圆柱形耦合振荡器阵列主波束位于θ=0°，φ=30°和θ=20°，φ=50°时的天线远场方向图。

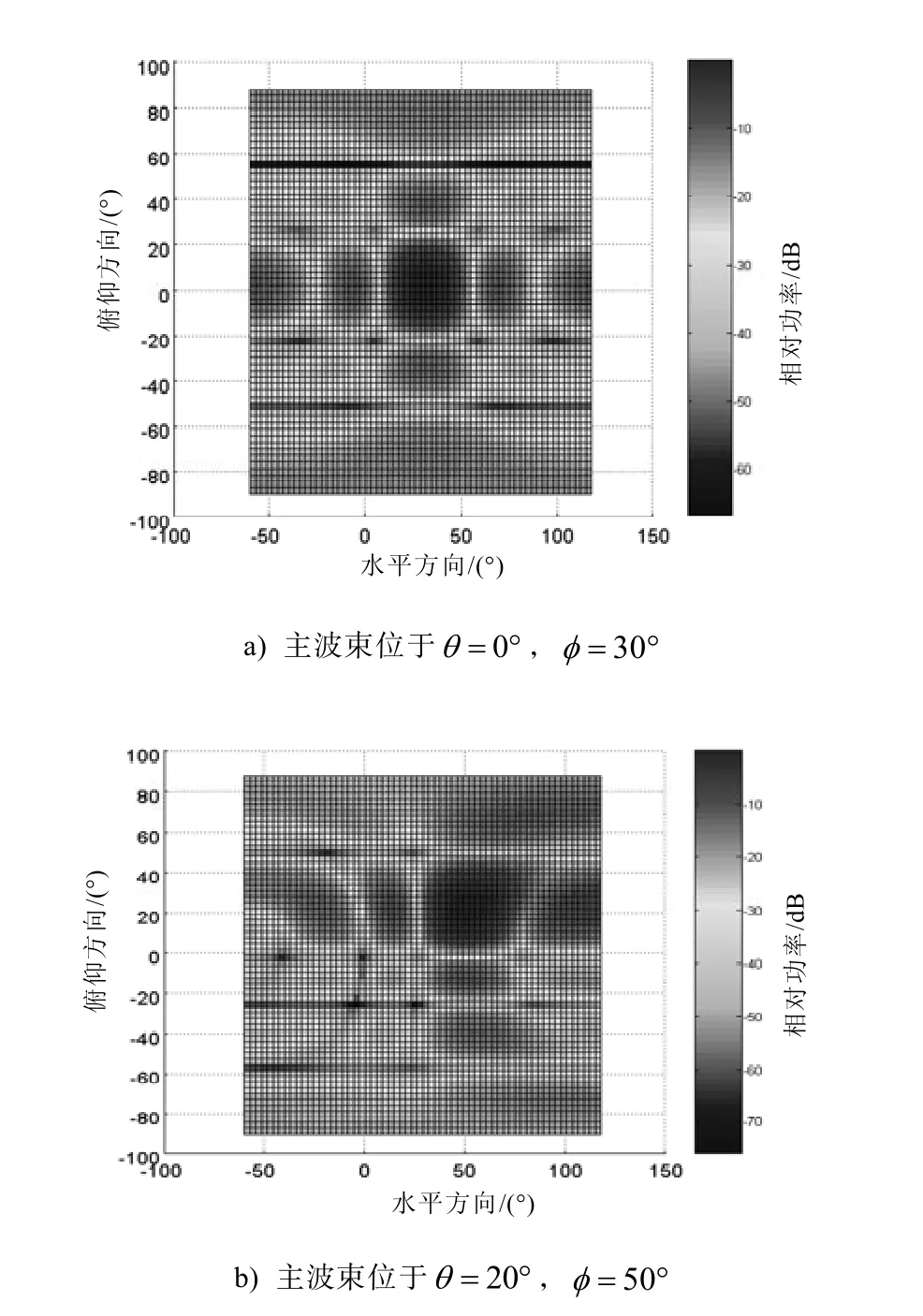
图6 圆柱形耦合振荡器阵列天线方向图

4 结论

本文研究了具有任意拓扑结构的曲面耦合振荡器阵列。通过分析发现当阵列中振荡器自由振荡频率任意分布时，如果单元间耦合强度满足一定条件，那么稳态时相位方程存在唯一的解，并且是稳定的，阵列单元间的相位差稳定在之间，说明任意拓扑结构的耦合振荡器阵列有可能实现共形相控阵天线的空间波束扫描。

[1]KAI CHANG,ROBERT A YORK,PETER S HALL,et al.Active integrated antennas[J].IEEE Transactions on Microwave Theory and Techniques,2002,50(3)∶937-944.

[2]YORK R A.Nonlinear analysis of phase relationships in quasi-optical oscillator arrays[J].IEEE Transactions on Microwave Theory and Techniques,1993,41(10)∶1799-1809.

[3]RONALD J POGORZELSKI.A 5-by-5 Element coupled oscillator-based phased array[J].IEEE Transactions on Antennas and Propagation,2005,53(4)∶1337-1345.

[4]RONALD J POGORZELSKI.On the steady-state phase distribution in a hexagonally coupled oscillator array[J].IEEE Transactions on Antennas and Propagation,2005,53(12)∶4058-4064.

[5]TED HEATH.Simultaneous beam steering and null formation with coupled[J].Nonlinear Oscillator Arrays.IEEE Transactions on Antennas and Propagation,2005,53(6)∶2031-2035.

[6]RONALD J POGORZELSKI.Phased arrays based on oscillators coupled on triangular and hexagonal lattices[J].IEEE Transactions on Antennas and Propagation,2004,52(3)∶790-800.

[7]TED HEATH,ROBERT KERR.Two-dimensional nonlinear oscillator array antenna[C]//IEEE AC paper#1070∶Version 6.2004∶1-12.

[8]张光义.相控阵雷达系统[M].北京∶国防工业出版社,1994∶59-66.

[9]RICARDO A OLIVA,STEVEN H STROGATZ.Dynamics of a large array of globally coupled lasers with distributed frequencies[J].International journal of Bifurcation and Chaos,2001,11(9)∶2359-2374.

[10]叶其孝,沈永欢.实用数学手册[K].北京∶科学出版社,2002∶799-816.

[11]ALI JADBABAIE,NADER MOTEE,MAURICIO BARAHONA.On the Stability of the Kuramoto Model of Coupled Nolinear Oscillators[C]//American Control Conference.2004∶4296-4301.