运用图示技巧处理高中地理教学中的难点
2012-03-22广东省东莞市第六高级中学523420覃纯乐
广东省东莞市第六高级中学(523420) 覃纯乐
运用图示技巧处理高中地理教学中的难点
广东省东莞市第六高级中学(523420) 覃纯乐
地理学科的空间性特点决定地理高考试题的最大特色是“无图不成题”或者“无图考图”。这就要求学生能够正确解读地理题目中的图形信息,但这正是大部分学生感到困难之处,从而成为制约其解题的一大瓶颈。在高中地理教学中,我们常常会遇到各种逻辑推理强、空间跨度远、理解难度大的一些问题,由于学生心理地图没有构建好,因而图文分家,地物分家,死记硬背,费时多、效率低,稍记即逝的现象严重。其主要原因是:头脑中没有形成清晰的地图表象,空间概念模糊不清,学习如无源之水,无本之木。因此,重视构建学生心理地图,利用地图发展学生思维,帮助学生巩固知识,是提高课堂教学效率的有效途径之一。笔者在几年的教学中不断实践研究,认为可以运用以下几种图示技巧来解决高中地理教学中的难点。
一、“直角三角形法”——直观呈现正午太阳高度角
正午太阳高度角问题在高中地理各类考试中常有出现,不少学生对太阳高度的理解颇有困难,遇到计算题更是丢分严重,常用的正午太阳高度计算公式是H=90°-∣φ-δ∣(H为所求地点的正午太阳高度,φ为所求地纬度,δ为直射点纬度,夏半年取“+”,冬半年取“-”)或:H=90°-纬度差(所求地与太阳直射点的纬度距离)。然而套背公式容易出现错漏。在这类问题中,我们可以通过“直角三角形法”即可轻松解决。
方法如下:
①绘制一条直线表示地平线(也可以看成一条经线),在线的两端分别标出“南北”方向;
②垂直于地平线画出太阳直射光线;
③标出观测者的位置并画出太阳光线,该光线与地平线的夹角即为当地的正午太阳高度角(用H表示);
④两条太阳光线的夹角用θ表示(θ为直射点与观测点的“距离”,即纬度差)。(见图1)
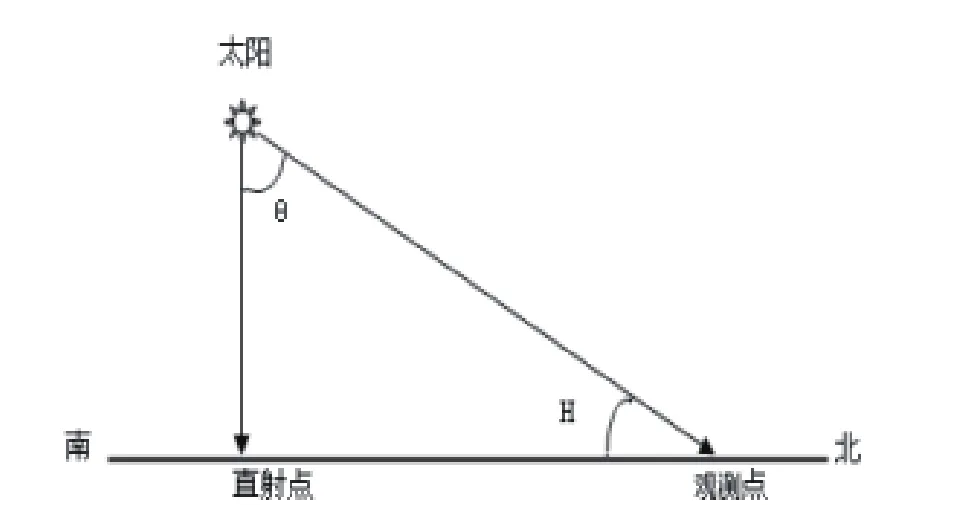
图1
例题1:
下图中L表示北半球某地太阳高度角的日变化状况。读图,回答下题。
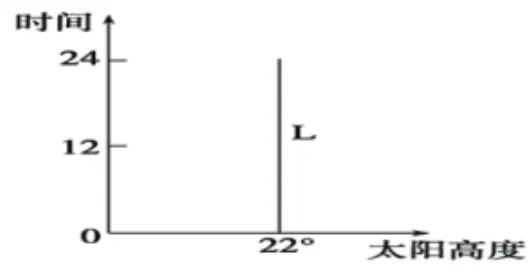
图2
此日某中学校园内(约36.5°N)的正午太阳高度角约是
A.32.5° B.75.5° C.45.5° D.66.5°
解题思路:
①分析L得出此日内北半球某地太阳高度在一天内没有变化,说明该地是北极点;
②从图2中读出北极点的正午太阳高度角为22°,利用“直角三角形法”可推出当日太阳直射的纬度是22°N;
③再次利用“直角三角形法”即可求出当日此校园内正午太阳高度角是75.5°。(见图3)
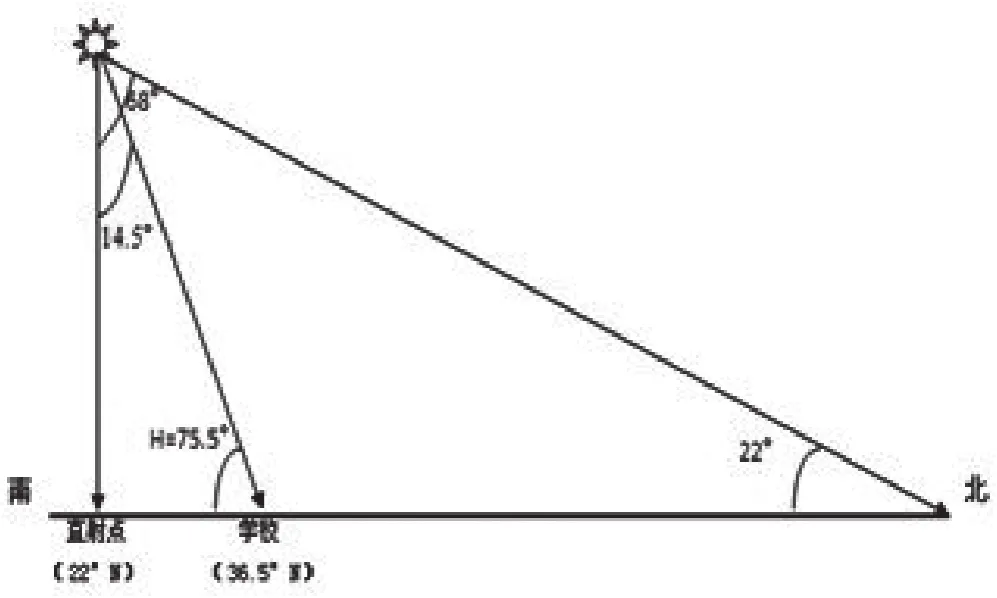
图3
例题2:
哥伦布航海期间,每天都用船上的象限仪观察北极星,只要数据为28°,他就坚信自己航向正确。读“哥伦布航海线路图”和“所使用的象限仪图”,完成下题。
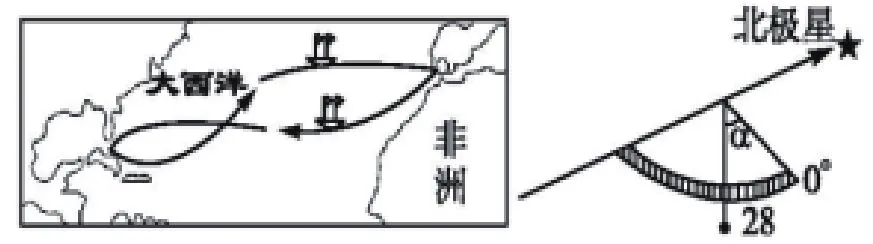
图4
按哥伦布的最初计划,他将一直沿
A.4°34'N航行 B.28°N航行
C.41°34'N航行 D.62°N航行
解题思路:
此题是利用象限仪观察北极星的高度角,我们可以参照求正午太阳的高度的方法来解此题。步骤如下:
①把北极星看成永远直射北极点的“太阳”;
②象限仪的读数即为观测者观测北极星的仰角;
③θ=90°-H=62°,即观测者距离北极点的纬度差为62°,观测者的纬度为28°N,此题得解。
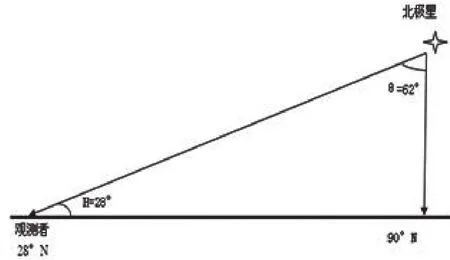
图5
二、“特殊经线”导航——提高空间定位能力
重视地图教学,关注地理区域的空间问题,区域地理在教学中很大程度上是通过区域地图来展现的,即区域地图是区域地理的重要载体。因此区域地理从根本上看就是要建立区域空间位置的概念,提高解决区域空间问题的能力。根据经纬线判断空间位置是地图空间定位的重要途径之一,也是解决其他综合地理问题的前提。在经纬网中,多数学生对特殊纬线(如:赤道、回归线和极圈)的空间位置较为熟悉,而对经线的空间位置生疏,从而影响地理空间位置的正确定位。因此,教学中应研究经线的位置特征,突出经线的定位价值。
1.世界地图:
以 0°经线为起点,往东共有6条特殊经线(包括0°经线、3条东经线、2条西经线),必穿过某个大洲的中部或大洲边界的附近(或重要地形区,如图6所示)。

图6
以0°经线为起点自西向东依次为:0°经线——穿过欧洲、非洲的西部;90°E经线——穿过北亚的西部、孟加拉湾; 120°E经线——穿过北亚的中部、中国东部沿海、台湾海峡、马来群岛中部、澳大利亚大陆西部;150°E经线——穿过北亚的东部、澳大利亚大陆东部;120°W经线——穿过北美洲的西部;60°W经线——穿过北美洲的东部、南美洲的中部。
2.中国地图:
中国地图也有六条定位价值很高的特殊经线——80°E、90°E、100°E、110°E、120°E和130°E经线,它们或穿过重要地形区的中部或边界,如图7所示:
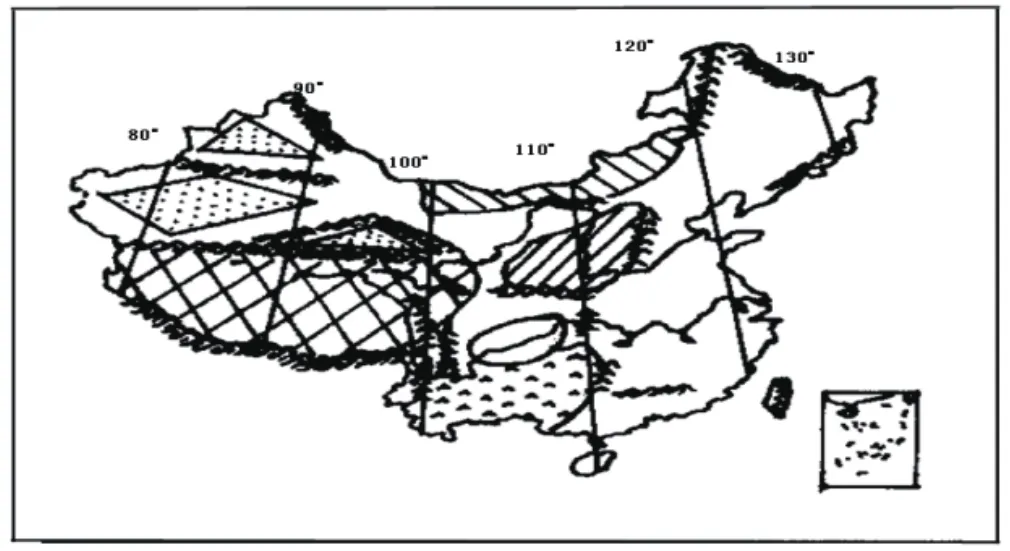
图7 中国主要地形区略图
80°E经线穿过准噶尔盆地和青藏高原西部边缘;90°E经线穿过准噶尔盆地、塔里木盆地东部边缘,又穿过柴达木盆地西部边缘和青藏高原中部;100°E经线穿过柴达木盆地和青藏高原东部边缘,又穿过内蒙古高原和云贵高原西部边缘;110°E经线穿过内蒙古高原和黄土高原中部,又穿过四川盆地和云贵高原东部边缘(还穿过海南岛);120°E经线穿过内蒙古高原、华北平原和长江中下游平原东部边缘,又穿过东北平原西部边缘(还穿过台湾海峡);130°E经线穿过松嫩平原和三江平原分界线附近。因此,世界地理和中国地理都各有六条具有很强的定位价值的经线,结合常用的特殊纬线,便可帮助学生在大脑中建立清晰的“脑图”,利用这个由特殊经线和特殊纬线构成的经纬网,许多空间定位的问题便可迎刃而解。
三、“数码排序”推力——还原地理动态过程
高中地理中有许多反映具有连续循环运动特征的图式,如“三圈环流示意图”等,这类图式往往比较复杂、空间跨度大,很多学生感到无从入手。“数码排序”的图示处理技巧可以解决这个问题,将连续循环运动的动态过程按其内在逻辑联系用数码进行编序,地理事物动态的运动过程便可“还原”出来。它对于帮助学生理顺地理事物运动过程的逻辑联系,启发学生思维有很大帮助。
“三圈环流”是高中自然地理知识的重难点,是学生丢分的“重灾区”。可将“三圈环流”进行数码排序——①表示赤道地区因受热膨胀上升气流;②表示赤道上空因受水平气压梯度力作用而流向高纬的气流;③表示气流②受地转偏向力影响而堆积在30°附近的上空,越堆越多从而被迫下沉的气流;④表示气流③达到地面后受水平气压梯度力作用而流向赤道地区的水平气流;⑤表示气流③达到地面后受水平气压梯度力作用而流向高纬的水平气流;⑥表示极地因冷却收缩而下沉的气流;⑦表示气流⑥达到地面后受水平气压梯度力作用而流向低纬的水平气流;⑧表示较暖的气流⑤和较冷的气流⑦在60°附近相遇而形成的上升气流(极锋)。这样,复杂的三圈环流图便有条理地展现出来,然后根据空气的水平运动和垂直运动推导出气压带和风带的分布规律。这种“数码排序图”的最大优点是能帮助学生强化地理过程的理解 (注:图中的数码排序是为了让学生学习方便,并不代表地理过程的必然顺序,如图8所示)。
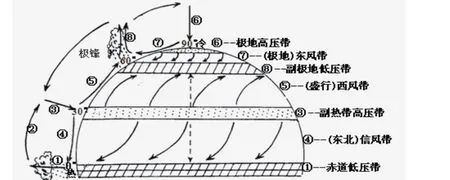
图8
四、“曲面拓扑”模拟——模拟等值线空间特征
在等值线“局部闭合圈”问题中,若相邻两条不同数值等值线出现一个局部闭合圈,则这个闭合圈的数值或等于相邻等值线的大值,或等于相邻等值线的小值;如果等于大值,那么局部闭合圈中间的数值更大,反之则更小(口诀是:高高低低或大大小小)。让学生理解这个规律难度很大,我们可以用形象具体的图示分析法来帮助学生理解掌握,做法是:以地形等高线为例,假设平面A(即地面)倾斜,则对应的等高线空间排列为相互平行的100m和200m等高面(如图9)。
使B区域拓扑变形为一个地形隆起,且超过一个等高距,则该隆起的部分与200m的等高面相交,形成200m的等高线闭合圈,其对应的等高线空间排列为相互平行的100m和200m等高线之间出现200m的等高线闭合圈(如图10)。相反,B区域向下凹陷且超过一个等高距,则会出现100m的等高线闭合圈(如图11)。
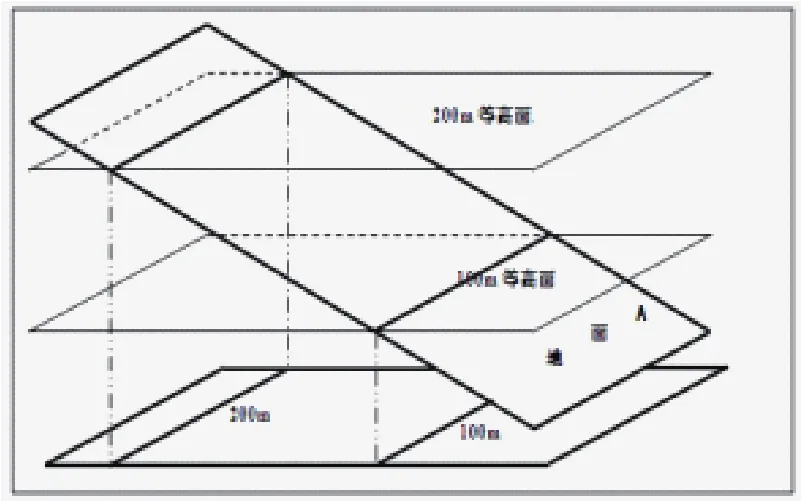
图9 等高面投影图
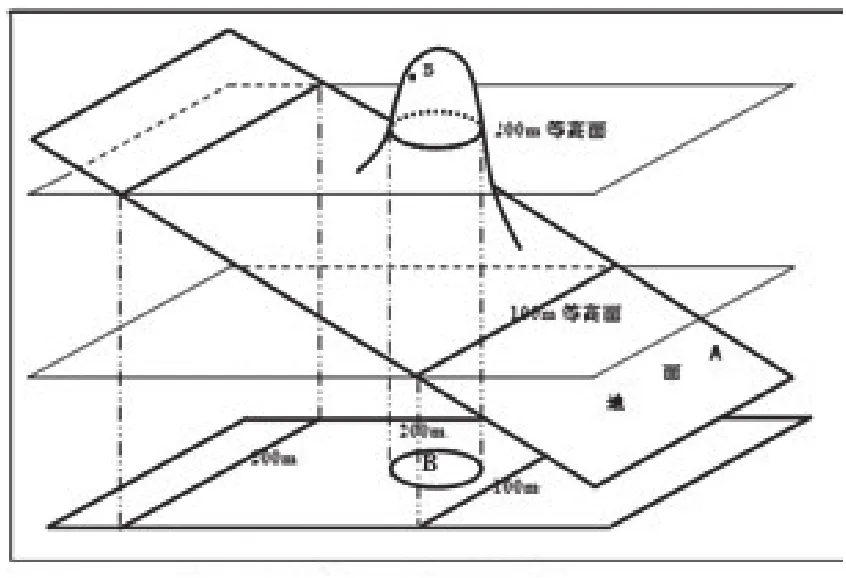
图10 等高面投影图
这种规律也适用于其它等值线分析。
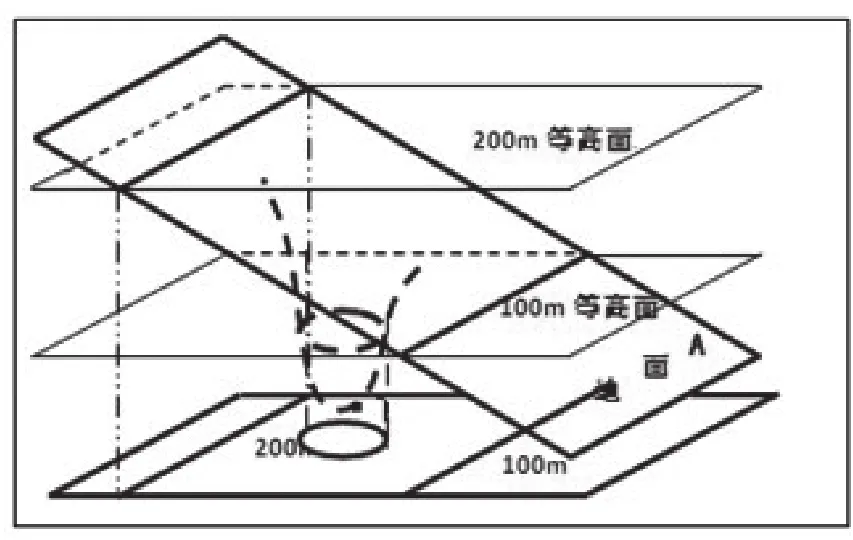
图11 等高面投影图
五、“理想模式”分析——建立地理规律模式
在实际教学中我们应该将繁杂的知识简单化、模式化和规律化,通过“理想模式” 分析,建立地理规律模式,真正体现地理学科的科学价值、实用价值,这样既可以提高学生学习地理的兴趣,又能提高学生驾驭地理知识的能力。
地理区域问题大多都是理想模式规律的区域化和复杂化,因此理想模式分析是地理分析的重要基础。对于地理分布和运动等复杂的知识系统进行优化处理,做到在“舍次取主、化繁就简、裁弯取直”的理想状态下进行模拟分析,使得分析出的理想模式图内容上逻辑严密,形式上简明美观,便于学生理解,为其它地理分析奠定基础。例如世界气候类型的形成和分布状况可设计为如图12所示的模式图。
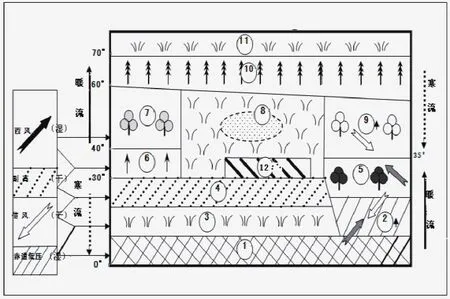
图12
假想大陆为一个长方形(以北半球为例),将大气环流、洋流、地形起伏等因素在图中相应位置标注,然后根据地理位置综合分析,这种较为简明并有成因线索的理想模式学生更容易理解掌握,一并掌握了自然带的分布规律。
