基于鲁棒控制理论的卫星姿态控制

刘海龙，李 隆，史小平

（哈尔滨工业大学航天学院，哈尔滨150001）

0 引 言

本文的研究对象是具有大惯量，且带有单翼大型挠性太阳能帆板的三轴稳定卫星，为了实现对日定向，需要太阳能帆板绕俯仰轴旋转，从而影响卫星的三轴稳定，需要对卫星的姿态进行主动控制。

在对系统控制器进行设计时，为考虑其主要矛盾，在设计时往往使用系统的简化模型或对模型进行线性化处理，从而引进了系统的未建模动态。而由于卫星中的燃料消耗以及太阳能帆板的转动等因素则会造成卫星转动惯量的变化，从而使得系统具有参数不确定性。此外，重力梯度力矩、太阳光压力矩、飞轮安装误差造成的力矩、挠性附件耦合力矩以及驱动太阳能帆板转动时的驱动力矩等，作为干扰源也为系统引入了不确定性［1－2］。

本文基于H∞控制理论，针对系统中存在的不确定性进行了控制器的设计，并对系统进行了仿真研究，结果表明采用H∞控制器较传统PID控制器具有更好的鲁棒稳定性和抗干扰性。

1 模型的建立

1.1 反作用飞轮下的动力学方程

在卫星姿态控制系统中，反作用飞轮参与下的卫星动力学方程可由如下方程描述［3］：

式中I＝ ［Ix，Iy，Iz］T，Ω＝ ［Ωx，Ωy，Ωz］T分别为飞轮的转动惯量和转速；Tx，Ty，Tz为外力矩。

考虑到卫星轨道角速度的数值较小，如果忽略其影响，即忽略三轴耦合作用的影响，并且这里假定卫星的角速度也很小，此时，则可忽略二阶小量及滚动、俯仰、偏航轴之间的耦合作用，式 （1）可化简为：

1.2 卫星姿态控制系统的简化模型

由式 （2）可知，带飞轮的系统动力学方程，经合理假设和线性化处理可简化为三轴解耦的形式。从而将3个回路视为单输入单输出系统分别进行设计。本文以俯仰控制回路为例进行设计，对于滚动控制回路和偏航控制回路可按类似的方法进行设计［4］。下面给出俯仰控制回路的系统框图，见图1。

由图1可见，卫星姿态的俯仰轴控制回路主要由4部分构成：能提供卫星俯仰轴姿态信息的姿态敏感器、俯仰轴回路控制器、反作用飞轮及挠性卫星的动力学环节组成。

其中，卫星刚体部分的传递函数用G0（s）表示，即：

式中Iy为卫星本体绕俯仰轴的转动惯量。

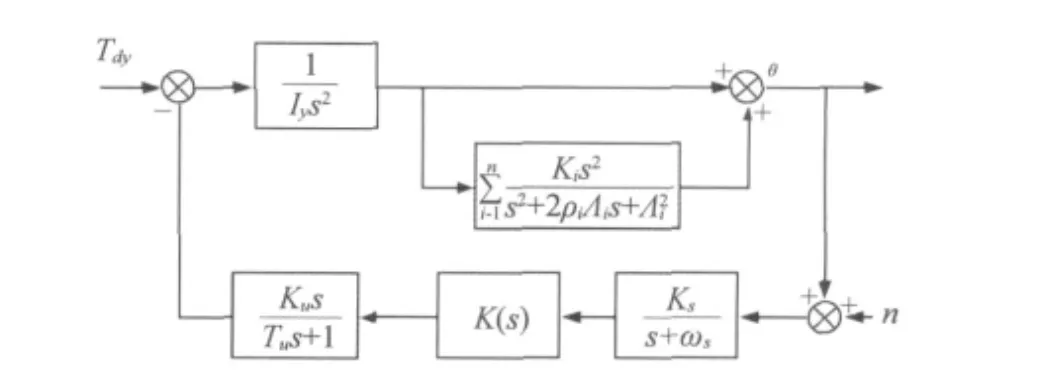
图1 俯仰轴控制回路简化框图Fig.1 Simplified block diagram for the pitch control loop

卫星的挠性环节部分可以视为在非约束模态下，由挠性结构的各阶模态相叠加组成，其动力学特性由式 （4）给出：

式中n为挠性结构模态的阶数；Ki，ρi，Λi分别为挠性结构第i阶模态所对应的模态增益，模态阻尼比及模态频率。

姿态敏感器的传递函数为：

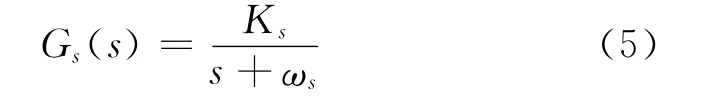
式中Ks为敏感器的增益；1／ωs定义为敏感器的时间常数。

工作在转速模式下的反作用飞轮经过简化处理，其传递函数可表示为：

式中Ku和Tu分别为反作用飞轮的增益和时间常数。

在本文的设计当中，将卫星的挠性环节视为乘性不确定性处理，而除控制器以外的其它各环节则组成了所谓的名义被控对象，用G （s）表示，即：

2 标准H∞控制模型的建立

考虑图1中的俯仰轴控制回路简化框图，设被控对象具有乘性不确定性［5］，即：

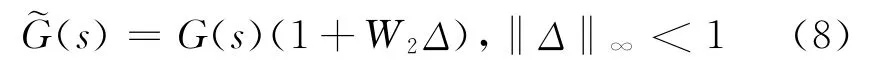
如图2所示，考察摄动界函数为W2（s）的干扰w1的干扰抑制问题。

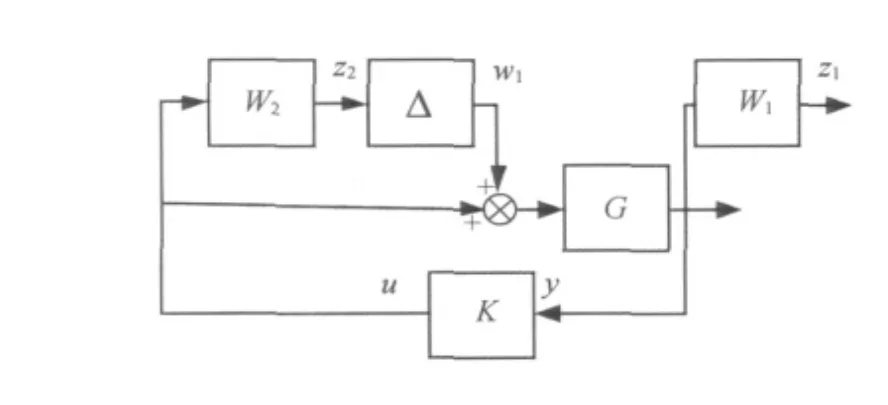
图2 姿态系统的干扰抑制问题Fig.2 Interference suppression problem of attitude system

在图2中，摄动Δ的输入为z2，输出为w1；z1为评价输出；y，u分别为控制器的输入和输出；W1，W2为加权函数。

首先，为保证系统的鲁棒稳定性，应满足式（9）所示的不等式：

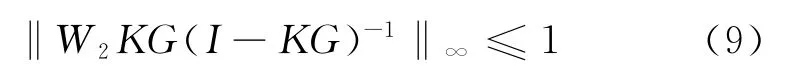
其次，为实现对干扰的抑制，需满足式 （10）所示的不等式：

定义 S＝（I－KG）－1，

分别称为系统的灵敏度函数和补灵敏度函数，满足S＋T＝I。则式（9）与式（10）所对应的H∞优化问题为：

为满足DJKF解法中对广义被控对象秩的要求［6］，本文在控制器的输入端引入一个很小的扰动w2，可取W3＝10－6。且在选取加权函数W2时，应注意使其分子与分母阶次相同，从而保证其状态空间实现中含有直通项D12。

此时可求得系统的广义被控对象为：

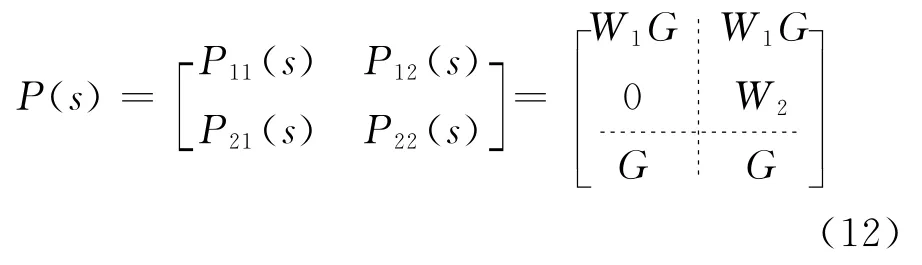
上述干扰抑制问题可等效为如图3所示的标准H∞控制问题，其中虚线框内为广义被控对象。

图3 标准H∞控制问题框图Fig.3 Standard H∞control problem block diagram

至此，已经建立起标准H∞控制问题框图，为下节通过选取加权函数进行控制器的求解做好了铺垫［7－8］。

3 控制器的求解

本文使用文献 ［9］所提供的卫星参数进行系统设计和仿真，各卫星参数为：

由以上参数可以求得名义被控对象为：

所使用飞行器挠性参数见表1。

挠性部件的各阶模态增益、模态阻尼比及模态频率可由理论计算得到，其中：

式中i为挠性模态阶数，也即表1中的行数。

经计算可得挠性部件各阶模态的参数。

表1 飞行器挠性参数Table 1 Flexible parameters of spacecraft

W1是代表系统干扰抑制性能的加权函数，本文的设计中要求控制器应包含有伺服补偿器也即积分环节，故W1应包含积分环节。为了照顾控制器中频段的频率特性，使积分环节不致影响其中频段特性，假设要求在0.2rad／s处积分规律应开始衰减掉［10］，所以综合以上分析，可选定加权函数为：

式中0.000 1是为了保证虚轴上无极点也即其对应的Riccati方程可解而引入的微小摄动；a为可调参数，通常来讲，在满足H∞次优设计问题的范数约束条件下，a一般取较大的值，以提高系统的干扰抑制性能。

W2是代表系统乘性不确定性的加权函数，要求具有低频增益小，高频增益大的特点。为减少设计的保守性，选取的W2应基本覆盖挠性结构摄动后的频率特性，本文要求所选W2可覆盖自然频率在±20%摄动下的频率特性，取为：

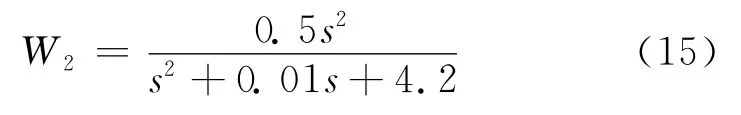
W3是为了满足P21（s）对秩的要求而引入的微小摄动，故W3应取一个微小的量，本文取为：

本文取a＝500，对应的γ＝1.006 9，此时求得的H∞控制器为：

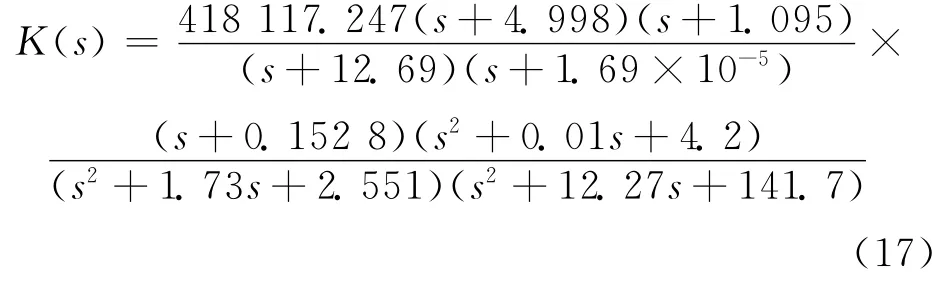
考虑到控制器中由式 （17）引入的摄动项0.000 1对控制器的影响，将控制器分母（s＋1.69 ×10－5）改写为s，则最终得到的控制器为：

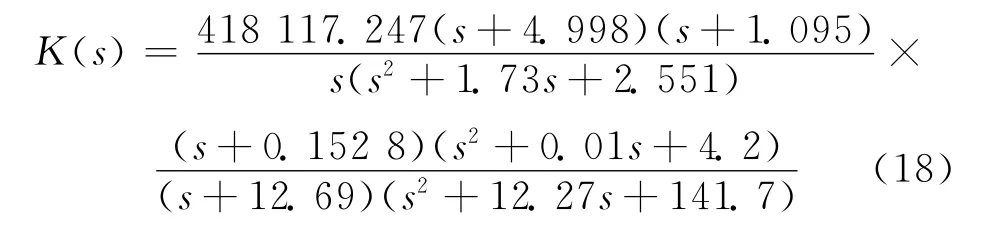
4 仿真分析与对比研究

4.1 奇异值分析

图4为表示系统灵敏度函数S与W1P关系的奇异值曲线，关系式‖W1GS‖≤γ代表系统的鲁棒性能，即对干扰的抑制能力。故应有关系式¯σ［S（jω）］＜γ¯σ［（W1（jω）G（jw））－1］成立，由图4可见，实线在虚线下方，满足¯σ［S（jω）］＜γ¯σ［（W1（jω）G（jw））－1］，这表明所设计的控制器满足了系统对鲁棒性能的要求。

图5为表示系统补灵敏度函数T与W2关系的奇异值曲线，关系式‖W2T‖≤γ代表了系统的鲁棒稳定性，即系统在乘性摄动下仍具有鲁棒稳定的特性。故应有关系式¯σ［T （jω）］＜γ¯σ［（W2（jω）－1］成立。由图5可见，实线在虚线的下方，满足¯σ［T （jω）］＜γ¯σ［（W2（jω）－1］，这表明所设计控制器满足了系统对鲁棒稳定性的要求。

4.2 鲁棒控制器与PID控制器比较

本文取最大外干扰力矩为：

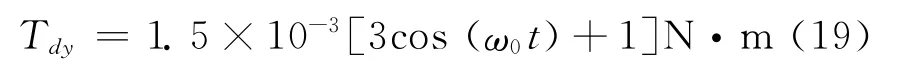
式中ω0为轨道角速度，设ω0＝0.001 08rad／s。仿真初始条件选为：θ（0）＝0.5°，θ·（0）＝0.01°／s。

图6和图7分别给出了鲁棒控制器作用下俯仰角和俯仰角速度的调节曲线。

选定PID控制器参数为Kp＝200，Ki＝2.32，Kd＝1 000。

图8和图9分别给出了PID控制器作用下俯仰角和俯仰角速度的调节曲线。

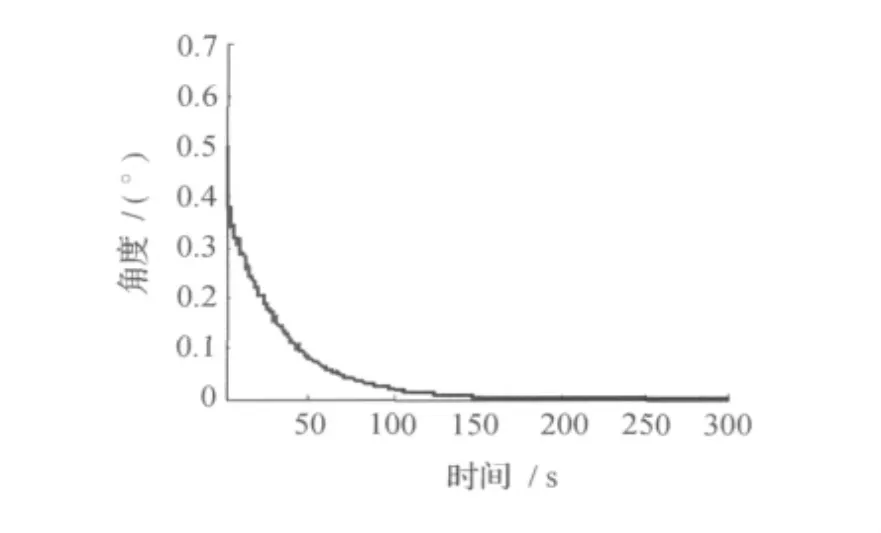
图8 PID作用下俯仰角的调节曲线Fig.8 Curve of pitch angle with PID control

5 结 论

本文应用鲁棒控制理论的分析与综合方法，对带挠性太阳能帆板的三轴角动量飞轮式卫星的姿态控制系统进行了设计，并对所设计的系统进行检验和仿真分析。解决了卫星姿态控制系统设计中的未建模动态和参数不确定性问题，所设计控制器可兼顾系统的稳定性和干扰抑制性能，与PID控制器相比，H∞控制器具有更好的鲁棒稳定性与鲁棒性能。

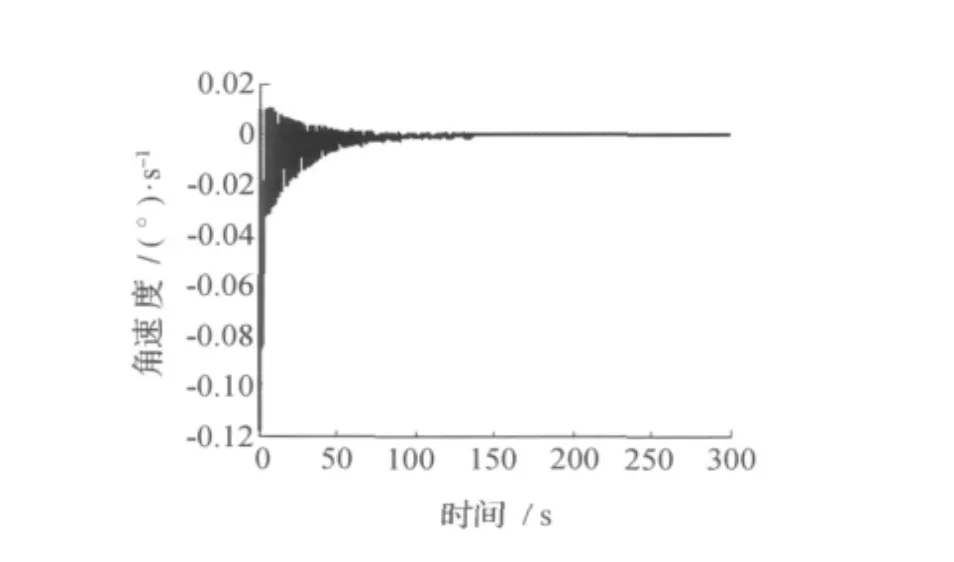
图9 PID作用下俯仰角速度调节曲线Fig.9 Curve of pitch angle velocity with PID control

［1］徐福祥.卫星工程概论 ［M］.北京：中国宇航出版社，2003：14－18.

［2］张志文.卫星姿态的鲁棒自适应控制方法研究 ［D］.哈尔滨：哈尔滨工业大学，2009.

［3］章仁为.卫星轨道姿态动力学与控制 ［M］.北京：北京航空航天大学出版社，2006：150－155.

［4］宋 斌，马广富，李传江.基于鲁棒控制的挠性卫星姿态控制［J］.系统仿真学报，2005，17（4）：969.

［5］梅生伟，申铁龙，刘康志.现代鲁棒控制理论与应用：第二版［M］.北京：清华大学出版社，2008：71－77.

［6］Doyle J C，Glover K，Khargonekar P P，et al.Statespace solutions to standard and control problem［J］.IEEE Transaction on Automatic Control，1989，34（8）：831－847.

［7］Yuichi C，Hiroshi S，Yoshitake Y，et al.On－orbit attitude control experiments using ETS－VI by control and two－degree－of－freedom control［J］.Control Engineering Practice，1998，6：1 109－1 116.

［8］Catherine V C，Gilles D，Sandrine L B.Low－order robust attitude control of an earth observation satellite［J］.Control Engineering Practice，1999，7：493－506.

［9］耿云海，崔祜涛，崔海英，等.挠性飞行器飞轮姿态控制系统设计［J］.系统工程与电子技术，2001，23（6）：57－58.

［10］Skullestad A，Gilbert J M.Control of a gravity gradient stabilized satellite［J］.Control Engineering Practice，2000，8：979.