基于边缘频率加权的Hausdorff距离人脸检测定位算法

赵永安，王国权，王荣豫

（1.黑龙江科技学院计算机与信息工程学院，哈尔滨150027；2.中国运载火箭技术研究院，北京100076）

0 引 言

在人脸识别的过程中，首要面对的问题就是如何将人脸从待检图像中分离出来。这是人脸识别研究的一个难点和热点。我们接触到的人脸图像，许多具有复杂背景且有姿态 （角度、表情、尺寸等）、遮罩 （如化妆、景物入侵等）、光照 （光源条件、阴影）等干扰因素，不仅影响人脸定位效果，甚至会造成定位错误。同时，在一幅待检图片中，不能期望其中只含有一个人脸［1］。而且，有些图像中人脸与躯干部分是连为一体的，因此如何将其从中提取出来也是一个令人深为困惑的问题［2］。

基于人脸模型的定位方法的主要特点是先建立人脸的模型，形成一定的模板。再通过对模板与待检图像的比较与搜索来对人脸进行检测定位。本文提出基于边缘频率加权的Hausdorff距离人脸检测定位算法，就属于其中的一种。

1 Hausdorff距离

1.1 Hausdorff距离的基本概念

由于进行识别的图像其基本单位都是像素［3］，可将这些像素视作一个个的点。于是，所谓人脸识别本质上就是人脸特征集 （点集A）在待检图像（点集B）中寻找某个特定区域的匹配过程。Hausdorff距离（Hausdorff distance，HD）就是用来定义点集间近似程度，同时用特征点集对于待检图像中需要找寻的部分进行搜索的一种人脸检测定位算法。设有点集A＝｛a1，a2，…，am｝与B＝｛b1，b2，…，bn｝，可构造Hausdorff距离为：

式中：

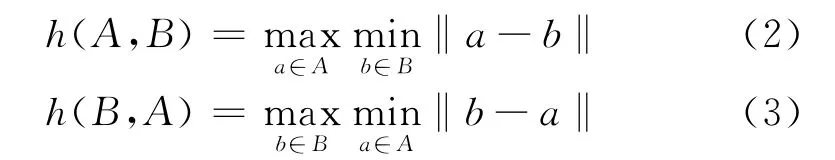
上两式中，范数‖·‖形式可以不固定。其中h（A，B）称做由点集A至点集B的有向Hausdorff距离。它的几何意义为由点集元素a∈A至点集B内任意元素的最大距离。同样，h（B，A）称作由点集B至点集A的有向Hausdorff距离。它的几何意义为由点集元素b∈B至点集A内任意元素的最大距离。由于h（A，B）与h（B，A）不对称，因此取它们中的最大值确定为点集间的Hausdorff距离。Hausdorff距离的几何意义为：若存在点集A、B，其间的Hausdorff距离为d，则其中一个点集中的点将投射于另一个点集以任意一点为中心、半径为d的圆形域中。若它们的Hausdorff距离等于0，则其为重合。

1.2 改进的Hausdorff距离（MHD）

由于以上所构造的Hausdorff算法缺点是鲁棒性差［4］，有人将其中的最大距离用平均距离来替换，这就是改进的Hausdorff距离（modified Hausdorff distance，MHD），由式（2）和式（3）得：

其中NA为点集A内元素的规模；NB为点集B内元素的规模。把其代入式 （1）得：

将改进的Hausdorff距离算法用于待检图片与模板间比较，其优点为不用规定图片中特征区与模板一一对应，就可以较好地进行识别，系统裕度充足［5］；但其最主要的缺点是定位误差较大［6］，识别耗时较多［7］。

1.3 基于边缘频率加权的Hausdorff距离（EFWHD）人脸检测定位算法

1.3.1 基本概念

为解决上述方法的缺陷，采用了边缘频率加权的方法来对上述方法进行改进。在基于模板匹配的人脸检测定位方法中，需要预先建立人脸模板与图像中的人脸区域进行相关运算，在这个过程中需要考虑对模板进行坐标变换 （平移、旋转或伸缩）。而为了衡量匹配的程度，需要计算坐标变换后的人脸模板与图像中的人脸区域间的距离。实际使用人脸模板中的人脸边缘图像，与待检图片中的人脸区域对应边缘点集合间的匹配，匹配的点可用SUSAN算子检测［8］。

Hausdorff距离在人脸检测定位中常用作衡量匹配的程度。用Hausdorff距离来计算两个点集之间距离时，并不需要对两个点集的点之间建立一对一的对应关系，所以很容易实现。实际中，常对基本的Hausdorff距离进行各种改进［9］。

当借助Hausdorff距离来计算两个点集之间的距离，并与人脸模板进行匹配时，由于人脸区域中不同位置对匹配的贡献不同，可考虑对Hausdorff距离中的各项分别进行加权，即可以将式 （4）改为：

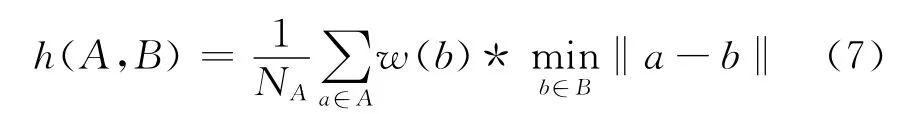
式中w （b）为权值函数，每个点b对应一个平面位置（x，y）。

权值函数可利用训练集来确定，但选取训练图像的哪些信息来确定权值函数有不同方法。例如，权值函数可利用图像灰度值来确定。此时由于原始的Hausdorff距离是定义在两个二值点集上的，所以需要先将灰度图像 （利用取阈值法）转化为二值图像。不过这种转化常会丢失一些信息，不能完全地反映图像上各点对人脸匹配的重要性［10］。

另一种方法是通过统计人脸图像中边缘信息来确定权值函数。例如可用边缘点出现在每个位置的频率来确定权值函数，即在那些边缘点出现频率较高的位置，如眼睛、嘴唇和人脸轮廓的边缘处，赋予较高的权值。这样得到的权值函数能够更直接有效地反映人脸的结构信息。

1.3.2 构造基于边缘频率加权的Hausdorff距离的人脸检测定位算法

1.3.2.1 权值函数的选取与EFWHD函数的确定

基于以上论述，可以构造用于在待检图像中搜索并定位人脸的模板，并构造EFWHD函数。其步骤如下：

1）对训练集内人脸图像做归一化预处理 （图片规格以及灰度归一化）。

2）使用SUSAN算子求出训练集内人脸图像的边缘图像E（x，y）。

3）对边缘图像E （x，y）进行阈值化计算，求出其二值图像B（x，y）。其中，选择阈值的标准是能够让B（x，y）内的值为1的像素点占图片总面积的20%，让所得的二值图像对于识别的作用一致［11］。

4）对B（x，y）能够构造权值函数w（b）如下：

式中M表示训练集内人脸图像集规模；Bi（x，y）为训练集中第i幅图像求出的二值图像位于 （x，y）上的对应值。

故所构造权值函数与训练集中各图像中对应位置处找到边缘点频率数成正比关系。将式 （8）代入式 （7）中，即可求得基于边缘频率加权的Hausdorff距离（edge frequency weighted Hausdorff distance，EFWHD）。

1.3.2.2 定位模板的构造

利用所构造的EFWHD算法，能够构造人脸检测定位的模板 （图1（a））。

1）样本集的构造：在选择用于构造模板的人脸图片样本集 （训练集）时，选择正面人脸做为样本集中的元素。

图1 EFWHD人脸边缘模板获取过程及人脸模板Fig.1 EFWHD face edge template for process and face template

2）人脸区域的归一化：手动标定图片中两只眼睛和两侧嘴角的位置，并将人脸图片尺寸分别归一为50×50（像素）。

3）灰度归一化：为了减少光度变化对于模板的影响，在尺寸归一化后，对图片的灰度值进行归一化，使之平均灰度值等于100，标准偏差为50。

4）去噪：利用高斯滤波器对人脸图像去除噪声。然后使用直方图均衡来补偿由于照明亮度不同以及拍摄设备的差异对成像效果造成的差异。

5）对经上述1）～4）步处理之后所得的人脸图像集利用SUSAN算子进行边缘检测，得到人脸边缘区域图像集。

6）对5）中所得人脸边缘区域图像集中的图像进行加权平均，形成人脸部加权平均概率灰度图（图1（b））。

7）对6）中进行二值化，得到人脸边缘特征二值图（图1（c））。

图1（b）表示边缘点在某一位置被找到的概率灰度图，其中较亮点表示人脸边缘点在这里被找到的几率较大。对图1（b）进行二值化处理可得人脸边缘特征二值图 （图1（c）），其中白色点代表图像的边缘点。经这样处理后，得到了用于在待检图像中搜索并定位人脸位置的模板 （图1（c））。

1.3.2.3 在待检图像中搜索并定位人脸

对待检图像进行归一化、平滑去噪等预处理。对预处理后所得的图像利用SUSAN算子提取边缘信息，然后对边缘图像进行二值化处理，再利用模板 （图1（c））在二值图像中对目标区域进行搜索，定位出人脸区域 （人脸区域用白框标出，眼睛位置用白色十字线标出）。

图2为将上述算法用于人脸定位实验的具体流程及结果。

图2 人脸定位实验各步结果及最终结果图Fig.2 Face positioning experiment each step results and final results figure

2 对若干利用Hausdorff距离进行人脸检测定位方法的比较实验

基于原始Hausdorff距离（HD，见式（2）和式（3））、改进的Hausdorff距离（MHD，见式（4）和式 （5））以及本文提出的基于边缘频率加权的Hausdorff距离（edge frequency weighted Hausdorff distance，EFWHD），分别对人脸图像的位置进行定位检测。实验所用计算机CPU为2.0GHz，内存为512MB，实验平台为Microsoft Windows XP，编程工具为visual c＋＋6.0／MFC，编程语言为c＋＋／c。比较所用的图像共有2 007幅，包括BioID库中所有的1 521幅图像，加上从Cohn－Kanade库中选取的具有不同光照的486幅图像（640×490）。人脸模板随机从上述图像中选取了10%的人脸图像进行构建。

由于人脸图像库中人眼中心距离位置是不受图像尺寸大小与人脸边缘信息影响的，所以采用这一特征作为衡量算法性能的标志。在比较各方法的定位精度时采用了对眼睛检测的相对误差指标。这个相对误差指标定义为：

式中Clt和Crt分别为左右两个眼睛中心的预期值（手工标定）；dl和dr分别为左右两个眼睛中心的预期值与检测值的差［12］；Cle和Cre分别为左右两个眼睛中心的检测值 （图3）。

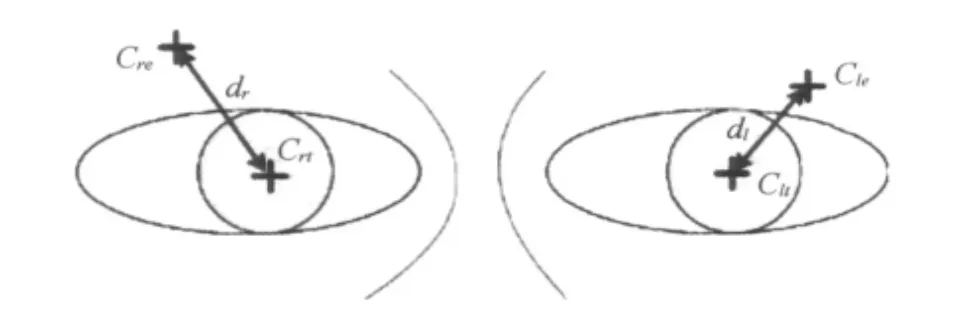
图3 人眼预期位置与测量位置间误差示意图Fig.3 Real eye position and position error measurement schematic diagram

比较实验共进行了40次，记录每一次的误差与耗时，并对平均误差以及平均耗时两个指标进行比较，结果见表1。

表1 利用Hausdorff距离（HD、MHD、EFWHD）进行人脸检测定位算法的平均误差及平均耗时对比Table 1 Using Hausdorff distance（HD，MHD，EFWHD）for face detection algorithm the average error and the mean time contrast

由表1可见，EFWHD比MHD误差要小，而MHD比HD误差要小，同时EFWHD平均耗时较少。

3 结 论

在本文中，笔者提出使用了一种基于边缘频率加权的Hausdorff距离定位检测算法，并将其与基于Hausdorff距离的定位算法和其改进算法进行了以人脸定位为目标的对比实验。经实验验证，文中所提出的基于边缘频率加权的Hausdorff距离人脸定位检测算法（EFWHD）具有精度较高且耗时较少的优点，性能较为优良。

［1］刘晓昊，章毓晋，谭华春.基于Hausdorff距离的相似性和对称性度量及在人脸定位中的应用 ［J］.信号处理，2008，24（1）：118－121.

［2］杜宇人，高浩军.基于车辆轮廓定位匹配的车型识别方法［J］.扬州大学学报：自然科学版，2007，10（2）：62－65.

［3］刘爱平，周 焰，关鑫璞.基于Hausdorff距离和改进ASM的人脸跟踪方法 ［J］.计算机应用研究，2007，24（10）：172－175.

［4］冷雪飞，刘建业，熊 智.基于分支特征点的导航用实时图像匹配算法［J］.自动化学报，2007，33（7）：678－682.

［5］陈秀宏，张伟伟，薛寺中，等.基于分块离散余弦变换和Hausdorff距离的人脸识别［J］.计算机应用，2010，（2）：86－89.

［6］徐 华.基于三维重构的人脸识别 ［D］.成都：成都电子科技大学，2009.

［7］SIM.D.G，PARK.R.H.2Dobject alignment based on the robust oriented Hausdorff similarity measure［J］.IEEE Traction on Image Processing，2001，10（3）：475－483..

［8］Gao，Y.，Leung，M.K.H.Line segment Hausdorff distance on face matching［J］.Pattern Recognition，2002，35（2）：361－371.

［9］刘福新.基于视频驱动的卡通人脸动画研究 ［D］.贵阳：贵州大学，2008.

［10］高 晶，孙继银，刘 婧.基于邻域灰度信息的Hausdorff距离图像匹配方法 ［J］.计算机应用，2011，（3）：741－744.

［11］M.Dubuisson，A.K.Jain.A modified Hausdorff distance for object matching proceedings［J］.International Conference on Pattern Recognition A，1994，12：566－568.

［12］O.Josorsky，K.J.Kirchberg，R.W.Frischholz.Robust face detection using the Hausdorff distance［A］Proceedings of Third International Conference on Audio－and Video－based Riometric Person Authentication［C］.2001：90－95.