微电火花加工中探针与工件中铁元素作用机理研究

陈志舜，何道伟，李 勇，王利光

（1.江南大学理学院，江苏 无锡214122；2.清华大学摩擦学国家重点实验室 微纳制造分室，北京100084）

0 引 言

随着在世界范围内微型化、精密化产品的不断发展，微细电火花加工 （MEDM）技术［1－5］正在以其高精度、超精细以及与所加工材料的机械性能无关等众多优点，在航空航天、医疗设备、微电子、信息技术、模具和新材料等众多技术领域内广泛应用。目前微细电火花加工技术已逐渐步入实用化阶段，其原理是利用电极发射的电火花脉冲产生的电场能，通过侵蚀材料而达到加工的目的。其特点是可控性好且所加工单位极小，与常规技术相比，大大提高了其加工精度和表面质量［6－8］。

由于精密加工要求逐渐微细化，通过实验观察现象时，因为微小的放电间隙，且浸没在工作液中，变得非常困难，使得微细电火花加工机理的研究发展较为缓慢。另一方面，以相似原理、模型分析等为基础的计算机仿真技术在精密加工中得到了广泛应用，为精密、超精密加工技术的研究提供了强有力的工具和手段［9］。

本文重点研究电火花加工中探针电极与工件中铁元素的相互作用机理，通过大数值计算和功能模拟，分别得出了外加面电极和体电极时的电子传输谱、态密度、分子能谱以及能量，并对所得结果进行了对比分析。

1 模 型

在建模过程中，以45＃碳钢作为构建模型标准，表1为45＃碳钢的化学组分。由表1可见，铁元素是碳钢中含量最多的元素，故而本文选择了铁元素作为对象，研究电极探针与工件中铁元素的作用机理。基于此，通过ATK软件构建了一个完全由铁元素组成的工件与加工电极的模型，以便分析铁元素在整个电火花加工过程中所起的作用。

表1 45＃碳钢的化学组分Table 1 Chemical components of 45＃carbon steel

在构建工件时，使铁原子之间的距离保持在0.25nm，该距离为刚好使得Fe－Fe之间成键的距离。在加工系统中由钨元素组成的电极顶端和工件表面的距离控制在刚好不能成键的范围内，约为0.28nm。这避免了因钨电极作用而引起的顶端吸附效应对工件原子结构的影响。模型的结构见图1。

2 计算原理与方法

计算时将系统温度设为1 000K，根据Landauer－Büttiker［10－12］理论，系统内电子的输运函数表示为：

式中GR（GA）是系统从激发点到反应点的延迟（超前）格林函数；E为入射电子的能量；ΓS（D）是耦合函数，可以通过扩展的Hückel方法计算得出。

此时输运函数可以表示为：

态密度的计算利用了下式：

图1 电火花加工模型Fig.1 EDM Model

在计算能带时用了Lohn－sham（K－S）方程［13－14］：

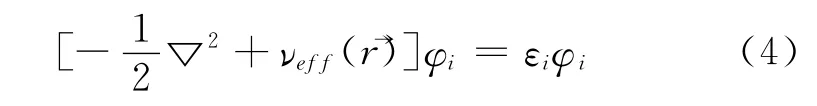
其中，有效势能为：

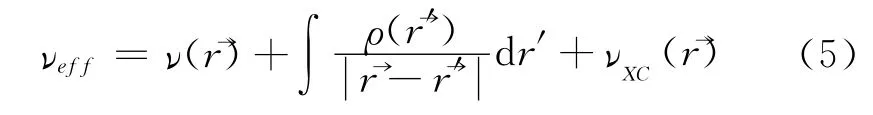
式中的电子态密度可以表示为：

通过自洽场 （SCF）方法求解，可以得出系统的能量为：

3 结果与讨论

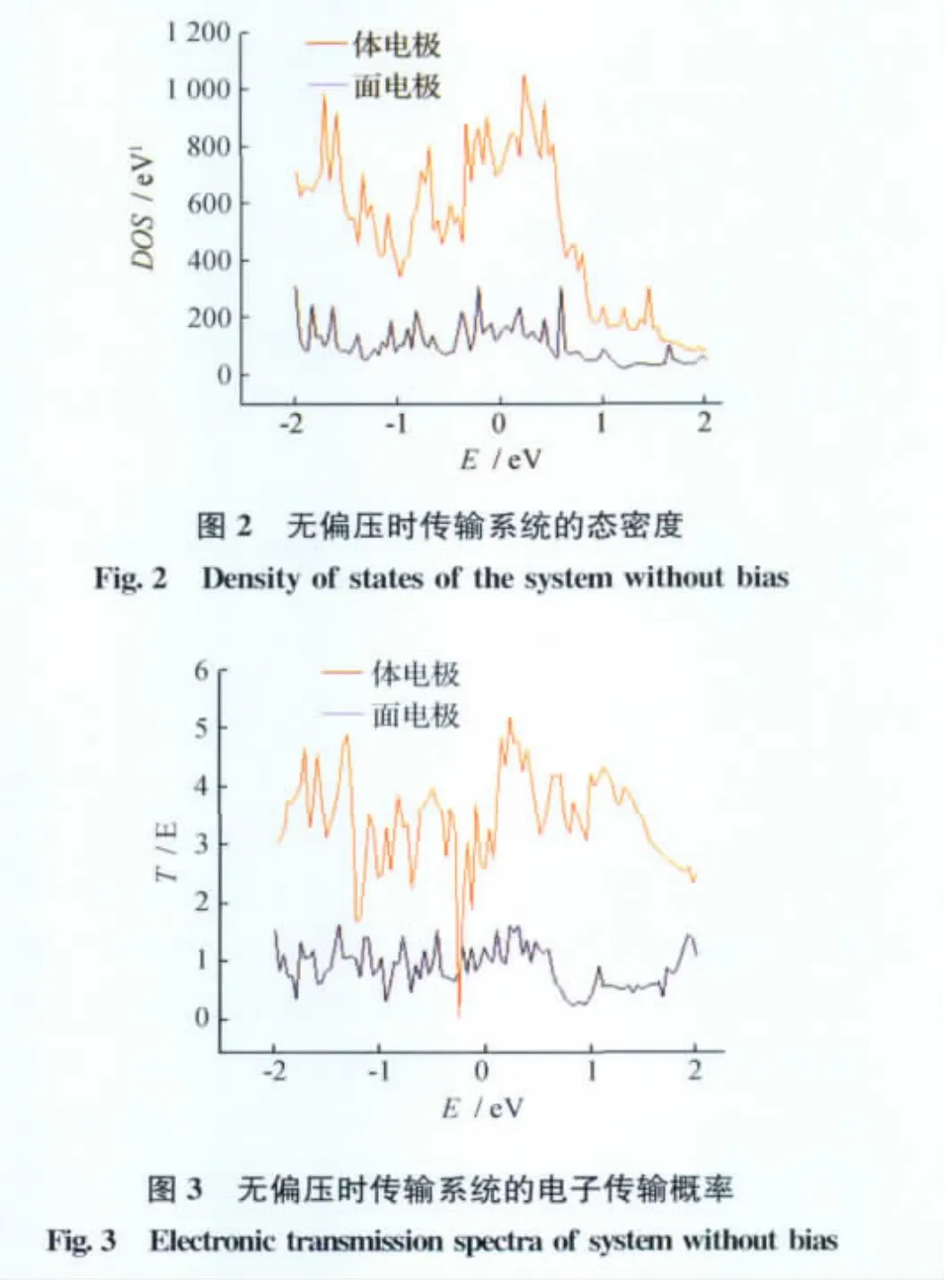
利用上面的模型和公式，首先对系统的电子传输谱和电子态密度进行了理论计算，其费米能级设置为0.0eV。当电极发射出电脉冲作用在工件上时，入射电子能量与铁原子发生共振时，会发生最好的电子传输状态。图2和图3分别为工件在外加面电极和体电极时加工系统的态密度与电子传输谱。由图2可见，在加体电极时所得到的态密度明显大于加面电极时的态密度。由于态密度的大小在一定程度上反映了其在对应的能量点附近能级数的多少，所以得到的态密度越大，则说明在态密度对应的能量点附近其本征能级就越多，电子出现的可能性相对就越大，进而在这些能量点附近电子的输运特性就相对来说较好。因此，在加体电极时，更有利于整个系统的电子传输，对微纳电火花加工更有利。由图3可见，加体电极时的传输概率明显大于加面电极时的情况，这说明在加体电极时，电子穿过体系的概率更大，更有利于提高加工效率。另外，对于同一传输体系的传输谱和态密度进行比较可知，电子态密度与传输谱线均具有脉冲型尖峰，其尖峰所对应的电子能量具有相同的位置，这也说明了在态密度较大的地方，其电子传输概率也较大，并且在峰值处发生共振传输。

通过理论计算，在外加面电极和体电极时与工件中的铁原子的相互作用分子能级被得出，结果见图4，同时得出了最高已占据分子轨道（HOMO）和最低未被占据分子轨道 （LUMO）的能量及能隙（Eg）和系统的总能量（Total energy），结果见表2。

图4 传输体系的能级Fig.4 Energy level of the transmission system

表2 传输系统的能级与总能量Table 2 Energy levels and total energies of transmission system ／eV

由图4和表2的结果可见，在外加体电极时，系统的HOMO、LUMO以及能隙均大幅减小，而由前线分子轨道理论［8］可知，分子的HOMO能级越高，则分子就越容易失去电子，而HOMO和LUMO之间的能隙则反应了分子从被占据分子轨道向未被占据分子轨道跃迁的能力，能隙越大，则电子就越不容易发生跃迁。因此，在外加体电极时，分子失去电子的能力比加面电极强，且更加容易发生跃迁。另外，通过总能量可以看出，在外加体电极时，总能量要大于外加面电极时的情况，这说明外加体电极时，从电极处放出的能量更大，更有利于工件的加工。

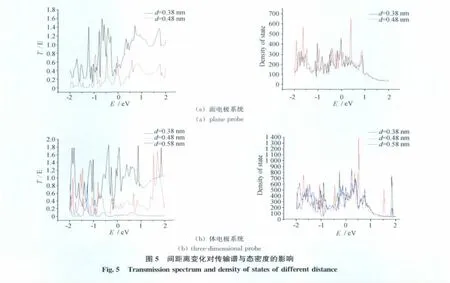
考虑到实际加工过程中电极不断运动的情况，本文还对电极与工件间距离的变化对电子传输和态密度的影响进行了研究，其结果见图5。其中面电极，距离分别设定为0.38nm和0.48nm；体电极的变化距离分别为0.38、0.48nm和0.58nm。从电子传输谱中可以看出，随着距离的增加，电子传输概率逐渐降低，特别是面电极在距离为0.48nm时，电子传输概率已＜1.0，几乎少有电子通过。而体电极在距离为0.58nm时，才没有电子传输。由此可见，体电极的极限加工距离要大于面电极，这也说明了外加钨体电极时，加工效果要更好一些。其次，分析态密度随距离的变化可知，随着间距离变大，态密度在多数能量点附近是降低的，电子出现的可能性也降低了，很显然这是完全符合物理实际的结果。

4 结 论

考虑到铁元素在许多工件中占最主要成分，研究中利用ATK软件，以铁原子为基组与加工电极构成基本加工模型，通过面电极和体电极的不同形式与工件的相互作用构成了电子传输体系。通过数值模拟与计算，得出了铁原子在外加面电极和体电极时体系的电子传输概率和电子态密度分布。结果显示在外加体电极时，电子穿过体系的概率比外加面电极时更大，更加有利于整个系统的电子传输，对微纳电火花加工过程更有利。另外还计算了传输系统的HOMO、LUMO及系统总能量，结果说明在外加体电极时，分子更容易失去电子，既电子更加容易发生跃迁。此外，研究显示面电极在电极与工件间距离为0.48nm时，电子的传输能力大大降低，系统处于近似截止状态，而体电极情况下间距达到0.58nm时电子传输才近似截止。本文的理论结果可以为进一步揭示微纳加工机理、改善和提高加工精度、探索更有效的电火花加工方法提供理论基础和技术支持。

［1］李 勇，佟 浩，郁鼎文，等.三维微细电火花伺服扫描加工工艺 ［J］.纳米技术与精密工程，2008，6（4）：307－311.

［2］付 伟，王先逵，曹凤国，等.微细电火花成形加工设备关键技术研究 ［J］.现代制造工程，2010，（4）：1－4.

［3］Chaitanya C.R.A，Ningyuan Wang，Takahata K.MEMS－based micro－electro－discharge machining（M3EDM）by electrostatic actuation of machining elec－trodes on the workpiece［J］.Journal of Microelectromechanical Systems，2010，19（3）：690－699.

［4］Takahata，K.，Gianchandani，Y.B.Batch mode micro－electro－discharge machining［J］.Journal of Microelectromechanical Systems.2002，11（2）：102－110.

［5］李 勇，李显军，周兆英，等.微细电火花关键加工技术研究［J］.清华大学学报：自然科学版，1999，39（8）：1－4.

［6］吕奇超，赵福令，王 津，等.微细电火花小孔加工过程仿真［J］.电加工与模具，2009，29（5）：14－17.

［7］张 勇，赵 航，张广玉，等.微细电火花加工系统及其工艺技术［J］.中国机械工程，2008，19（5）：526－530.

［8］赵万生，李文卓，王振龙，等.高精度微细电火花加工系统的研制［J］.电加工与模具，2004，（1）：6－8.

［9］Webzell S.That first step into EDM［M］.Findlay Publication Ltd，Lent，UK，2001.

［10］Haroon Ahmed，Michael Pepper，Alec Broers.Electronic transport in mesoscopic systems［M］.United Kingdom：Cambridge University Press，1999：119－125，148.

［11］Landauer R.Can a length of perfect conductor have a resistance［J］.Physics Letters A，1981，85：91－93.

［12］Büttiker M，Imry Y，Landauer L.Generalized manychannel conductance formula with application to small rings［J］.Phys.Rev.B，1985，31：6 207－6 215.

［13］W.Kohn，L.J.Sham.Self－consistent equations including exchange and correlation effects［J］.Phys.Rev.，1965，140（4A）：A1 133－A1 138.

［14］Predew J P，Wang Y.Accurate and simple density functional for the electronic exchange energy：Generalized gradient approximation［J］.Phys.Rev.B，1986，33：8 800－8 802.