机载武器传递对准的可观测性分析
2012-03-19战兴群张炎华
秦 峰 战兴群 湛 雷 张炎华
(上海交通大学航空航天学院,上海 200240)
随着科技的进步,武器制导的精度和速度要求也越来越高.初始对准作为武器制导过程中的重要因素,它的速度和精度将直接影响武器发射系统的反应速度与发射后的导航性能.捷联式惯性导航系统由于其不易受外界环境干扰被广泛应用于初始对准中.
机载武器初始对准过程中由于存在运动干扰,一般不采用自主式对准方法,而是利用机体上的主惯性导航系统(INS,Inertial Navigation System)或弹载的其它导航设备来对武器上的子INS进行初始对准[1].传递对准是利用机体上的主INS信息来动态匹配武器上的子INS信息来实现武器的快速对准,它具有较高的可靠性和稳定性.
传递对准过程中通常通过卡尔曼滤波器来实现子惯导失准角和器件误差的估计.状态估计的速度和精度决定着传递对准的速度和精度,而状态估计的速度和精度很大程度上取决于系统的可观测性[2].与此同时,在工程中过多的状态变量会增加处理器的计算负担,降低滤波实现的速度,加大卡尔曼滤波器实现的难度.因此,需要通过可观测性分析舍去对系统性能影响较小的状态变量,使工程上实现更加容易.
1 传递对准方案设计
传递对准是指利用子、主惯导系统输出的导航参数的差值作为量测量来估计出子惯导系统相对于主惯导系统导航参数误差和惯性元件误差,然后对子惯导系统进行初始校正的过程.
在理论上,可以利用运载体的主惯导和武器上的子惯导的多种参数进行匹配实现传递对准.根据匹配参数性质的不同,可以将传递对准匹配方法分为两类:一类是利用惯导计算的导航参数进行传递匹配,称为计算参数匹配法,如位置匹配法、速度匹配法;另一类是利用惯性元件测量参数进行传递匹配,称为测量参数匹配法,如加速度匹配法、角速率匹配法、姿态匹配法[3].测量参数法由于直接使用惯性元件测量值作为量测,其快速性要优于计算参数法,但其精度要低于计算参数法.本文采用“速度+姿态”的计算参数匹配方法实现传递对准,系统设计结构图如图1所示.

图1 传递对准系统结构图
2 传递对准误差模型
2.1 速度和姿态误差模型
速度+姿态的传递对准方法,以文献[4]提出的最具有代表性,现今被广泛使用.速度与姿态误差模型[4-5]如下所示:


其中,φm为姿态误差角;φa为安装误差角;为导航坐标系与武器载体坐标系间方向余弦矩阵;[δKa] =diag[δKaxδKayδKaz]和[δKg] =diag[δKgxδKgyδKgz]分别为加速度计和陀螺刻度系数误差;为挠曲运动引起的加速度误差;为挠曲运动引起的角速度误差;为导航坐标系与载体坐标系间相对角速度;和εs分别为加速度计与陀螺误差.
2.2 挠曲运动误差模型
载机在高速飞行运动过程中会受到外力以及自身机动动作的影响,机翼处于一种振动状态,它在各个轴上都存在变形,不能当作刚性模型来看.挠曲变形是指机翼受到空气动力及载机机动动作影响而产生的相对于机体的角运动,它会引起子惯导惯性敏感器件上产生相对于主惯导的角速度和加速度[6].在传递对准过程中为了消除挠曲变形带来的干扰,需要对它进行补偿.
挠曲变形的补偿通常是在滤波器中增加挠曲的状态变量来实现的,状态变量的建模通常采用二阶马尔科夫过程,以下为挠曲变形模型:
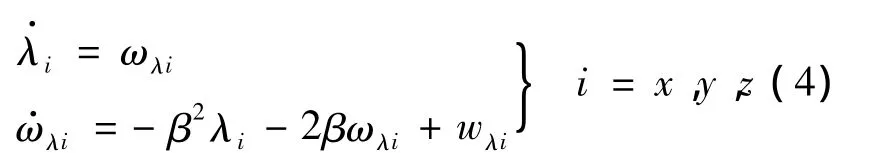
其中,λi为角变形;ωλi为相应的变形角速度;wλi为白噪声驱动,即为w的噪声强度.
3 传递对准系统设计
3.1 传递对准系统状态模型
在设计传递对准卡尔曼滤波器时,需要列写出描述系统动态特性的系统方程,线性时变系统状态方程如下:
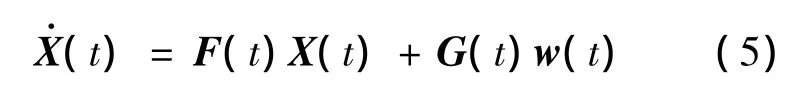
其中,X(t)为系统状态变量;w(t)为系统噪声;F(t)和G(t)分别为系统的状态和噪声系数矩阵.
选取的系统状态量和噪声如下:
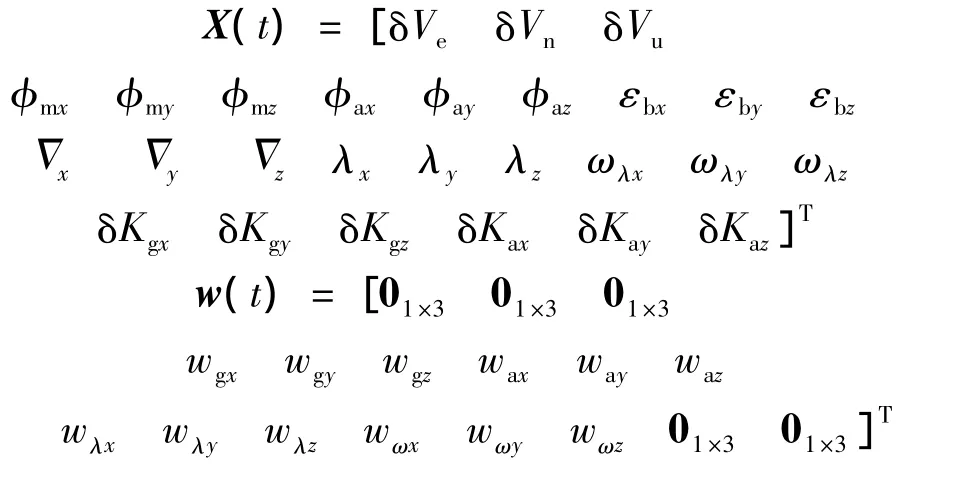
其中,wg为陀螺白噪声;wa为加速度计白噪声;wλ为挠曲角变形白噪声;wω为挠曲角速度白噪声.
3.2 传递对准量测模型
传递对准通常选择子惯导和主惯导之间的信息差值作为量测量,来校正子惯导的输出信息.本文采用“速度+姿态”的匹配法,以两个惯导系统之间的速度差值和姿态差值作为量测量.系统的量测方程和选择的量测量如下:
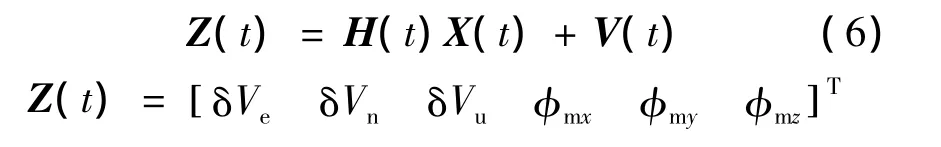
其中,Z(t)为量测量;H(t)为量测矩阵;V(t)为量测噪声矩阵.

4 传递对准系统可观测性分析
系统的可观测性分析是系统滤波器设计的一个重要环节,适当的可观测性分析可以简化滤波器,减小计算量,提高滤波效率.状态变量可观测性的强弱可以用可观测度来衡量.目前,可观测性和可观测度的分析主要有估计误差协方差阵的特征值法和可观测性矩阵的奇异值分解法.第1种方法由于需要在卡尔曼滤波运算之后进行,所以计算量较大,一般较少采用.奇异值分解(SVD,Singular Value Decomposition)法可以在滤波之前对系统进行可观测性分析,计算量较小,故被广泛采用[7].
在实际应用过程中,直接对线性时变系统进行可观测性分析比较困难.通常将整个时间分割成小的时间区间,在每个时间段里系统可近似地认为是线性定常系统,故称分段线性定常系统(PWCS,Piece-Wise Constant System).经过分析,本文采用基于PWCS的可观测性矩阵奇异值分解法对传递对准的线性时变系统进行可观测性分析.
假设Qs是系统的可观测性矩阵,Y为动态系统的观测值,X0是系统的初始状态.根据PWCS模型可以推出[8-9]:

根据奇异值分解法分解为以下形式[7,10]:

其中,U和V分别称为系统左奇异向量和右奇异向量;σ为矩阵Qs的奇异值;r为矩阵的秩.
当 U=[u1,u2,…,un],V=[v1,v2,…,vn]时,式(7)转换为
当观测量Y具有常值范数时,初始状态X0形成一个椭球,其方程为
其中1/σi表示此椭球主轴的长度.显然,该椭球的体积应该由奇异值决定,当奇异值越大时其体积越小,X0取值范围也越小,因此X0的上界可以表示为
如果σi的值越大,X0的取值范围就越小,卡尔曼滤波器对其估计的就越精确.所以系统状态变量对应的奇异值σi越大,其相应的可观测性能就越好;当σi=0时,状态变量完全不可观测.
系统状态变量的可观测性性能也可用可观测度进行评价,可观测度定义为
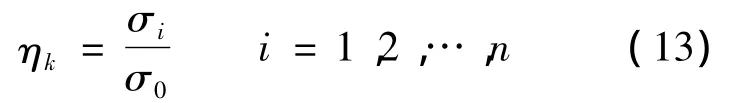
式中,ηk为第k个变量的可观测度;σ0为外观测量对应的奇异值;σi为使取得最大的奇异值.
5 仿真实验与结果分析
为了卡尔曼滤波器能够更好地估计出失准角,本文选择三轴摇摆的机动方式来实现传递对准.三轴摇摆运动是载体以正弦规律绕纵摇轴、横摇轴和航向轴摇摆,其数学模型如下:
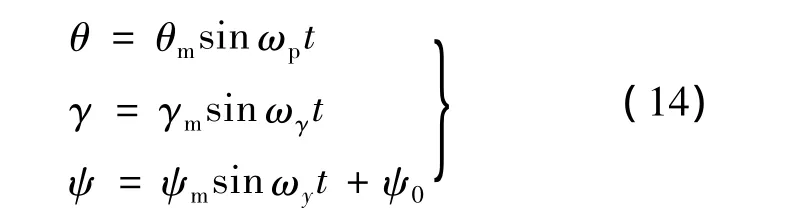
式中三轴摇摆的振幅均为15°,摇摆的周期为7 s,摇摆角频率 ωi=2π/Ti(i=p,γ,y),初始航向 ψ0仿真时取0°.
取10个时间段的可观测性矩阵进行分析,可以得到27个奇异值.根据式(10)可以计算出27个奇异值对应的状态变量初始值X0并画出直方图,从而得到各个状态变量的可观测性和可观测程度.状态变量的可观测性直方图如图2所示,图中状态变量的排序按照滤波器设计时顺序排列.

图2 传递对准状态变量可观测性直方图
由图2可见外观测量δVe,δVn和δVu的奇异值均为1,其可观测度也为1.状态变量 δVe,δVn,δVu,φmx,φay,φaz,εbx,εby,εbz,ωλx,ωλy和 ωλz可观测,状态变量 φmy,φmz,φax,λx,λy和 λz的可观测性较差,状态变量 Δx,Δ
y,Δz,δKgx,δKgy,δKgz,δKax,δKay和 δKaz完全不可观测.所以,系统有 18个状态变量可观测,9个状态变量不可观测.根据图2的可观测性分析可对机载武器传递对准的滤波器模型进行简化,去除不可观测的状态变量,减少滤波器计算量.简化后的滤波器模型如下:
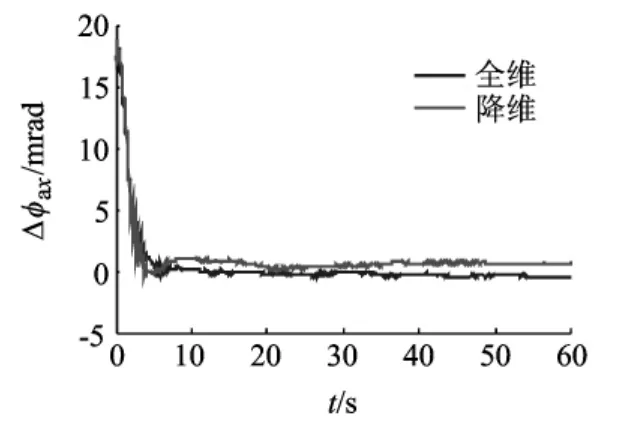
图3 x轴安装误差角估计的误差
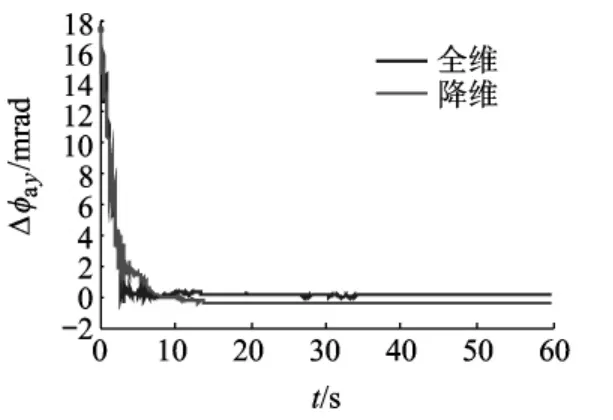
图4 y轴安装误差角估计的误差
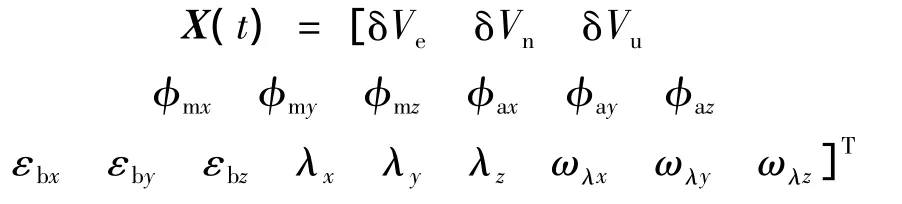
对降维前后的卡尔曼滤波器分别进行仿真,仿真结果如图3~图5所示.降维以后安装误差角估计的误差变大,但不明显;估计误差仍逐渐收敛,可以满足机载武器传递对准系统设计要求.因此,降维滤波器在大大降低运算工作量的同时仍可以满足系统要求,验证了可观测性分析的正确性和准确性.
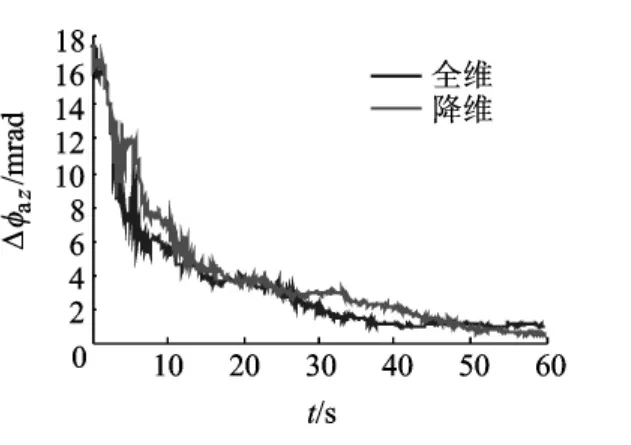
图5 z轴安装误差角估计的误差
6 结论
本文设计了“速度+姿态”匹配的机载武器传递对准系统.在PWCS理论的基础上,利用SVD奇异值分解法对系统的可观测性进行了分析,得到了系统状态变量的直方图.根据可观测性分析的结果对系统进行了降维,并对降维前后的滤波器性能进行了分析.发现通过降维系统在不影响其性能的情况下大大减小了运算负担,提高了工作效率.因此,充分证明了机载武器传递对准系统进行可观测性分析的必要性和正确性.
References)
[1]谢波.捷联惯导系统动基座初始对准技术研究[D].北京:北京航天第二研究院,2004 Xie Bo.Research on initial alignment of strapdown inertial navigation on moving base[D].Beijing:The Second Aeronautics Institute of Beijing,2004(in Chinese)
[2]房建成,周锐,祝世平.捷联惯导系统动基座对准的可观测性分析[J].北京航空航天大学学报,1999,25(6):714-719 Fang Jiancheng,Zhou Rui,Zhu Shiping.Observability analysis of strapdown inertial navigation system on moving base[J].Journal of Beijing University of Aeronautics and Astronautics,1999,25(6):714-719(in Chinese)
[3]顾冬晴.机载战术武器的传递对准及其精度评估技术研究[D].西安:西北工业大学精密仪器与机械系,2002 Gu Dongqing.Technology research of the transfer alignment and transfer alignment accuracy evaluation of airborne tactical weapon[D].Xi’an:Department of Precision Instrument and Machinery,Northwestern Polytechnical University,2002(in Chinese)
[4] Kain J E,Cloutier J R.Rapid transfer alignment for tactical weapon applications[R].AIAA-89-3581,1989
[5]王新龙,申亮亮,马闪.摇摆基座SINS快速精确传递对准方法[J].北京航空航天大学学报,2009,35(6):728 -731 Wang Xinlong,Shen Liangliang,Ma Shan.Transfer alignment of strapdown inertial navigation systems on rolling bases[J].Journal of Beijing University of Aeronautics and Astronautics,2009,35(6):728-731(in Chinese)
[6]丁滢颖.机载导弹的传递对准技术研究[D].西安:西北工业大学航天工程学院,2001 Ding Yingying.Research on transfer alignment technology of the missile on board the aircraft[D].Xi’an:School of Astronautics Engineering,Northwestern Polytechnical University,2001(in Chinese)
[7]万德钧,房建成.惯性导航初始对准[M].南京:东南大学出版社,1998:83-106 Wan Dejun,Fang Jiancheng.Initial alignment of inertial navigation[M].Nanjing:Southeast University Press,1998:83 - 106(in Chinese)
[8] Goshen-Meskin D,Bar-Itzhack I Y.Observability analysis of piece-wise constant systems[J].IEEE Transaction on Aerospace and Electronic Systems,1992,28(4):1056 -1067
[9] Ye P,Zhao H,Zhu R J.Estimation error of GNSS/SINS in-flight alignment through observability analysis[C]//International Symposium 2010 on GPS/GNSS.Taipei,Taiwan:IGNSS Society Inc,2010:227-231
[10]吴俊伟,孙国伟,张如.基于SVD方法的INS传递对准的可观测性能分析[J].中国惯性技术学报,2005,13(6):26-30 Wu Junwei,Sun Guowei,Zhang Ru.Analysis on observability of INS transfer alignment based on SVD method[J].Journal of Chinese Inertial Technology,2005,13(6):26 - 30(in Chinese)
