雷达对扩频通信系统干扰分析方法
2012-03-19谢树果
王 磊 谢树果
(北京航空航天大学 电子信息工程学院,北京 100191)
雷达的电磁辐射干扰分析是电磁环境评估和频谱管理的重要内容,对于在复杂电磁环境下实现雷达与其它电子信息系统的频率共享与电磁兼容、发挥各自的作战效能具有重要意义.传统的雷达干扰分析方法,如国际电信联盟 ITU-R M.1461-1和ITU-R M.1464-1建议中关于雷达对其它无线通信系统的干扰分析,从宏观的角度将雷达发射脉冲功率平均化,通过比较被干扰接收机前端的信干比与设备抗干扰门限的大小,从而确定干扰程度.文献[1-3]提出一种基于雷达电磁干扰时间离散性和数据链设计冗余能力的电磁干扰综合分析方法,通过天线耦合概率模型和干扰源与数据链间可能的最大耦合损失,可以计算出干扰概率和干扰脉冲数.上述方法归纳起来有两点不足:
1)没有充分考虑雷达瞬时峰值脉冲的干扰效应,使得干扰分析结果往往偏于保守;
2)未能细致地反映雷达脉冲长短对系统造成干扰的区别,从而无法从更深层次上揭示雷达对其它系统和设备干扰的机理.
近年来美国Ericsson等公司在其向国际电联提交的报告中将雷达分为短脉冲雷达和长脉冲雷达两种模式,在时域上讨论了2700~2900MHz频段5种典型雷达对IMT-2000/WCDMA系统的干扰问题,结果表明,在雷达信号功率不至于造成IMT-2000/WCDMA系统前端低噪放过载的情况下,短脉冲雷达信号对其的干扰基本可以忽略,长脉冲雷达的频率隔离度需保持在5MHz以上[4-5].
本文在上述研究的基础上,首先从时域上分析了脉冲雷达对直接序列扩频通信系统的干扰机理,推导出误码率公式并得出相应理论曲线;其次利用建立的雷达干扰分析模型,采用仿真方法得出短脉冲和长脉冲雷达分别在同频以及邻频情形下对扩频通信系统的干扰特性,通过与理论分析对比,两种方法得出的结果基本吻合;最后利用分析结果计算出了5种典型雷达与扩频通信系统的频率-距离隔离关系,为解决复杂电磁环境下雷达与扩频通信系统的频率协调和电磁兼容问题提供了较为科学的分析方法和途径.
1 雷达对扩频通信系统的干扰机理
雷达的工作频率一般可以从15~35×103MHz,最新技术的雷达已扩展到毫米波甚至亚毫米波范围[6].雷达对扩频通信系统的干扰途径主要有两种情况:
1)高达几千~几兆瓦的雷达信号经空间传播损耗后从天线进入扩频通信接收机,由于接收混频电路的非线性而形成的变频干扰;
2)雷达的谐波和非谐波辐射进入扩频通信接收机频带内对有用信号造成干扰.
本文着重从系统间电磁兼容的角度研究同频段或相近频段内的雷达对扩频通信系统形成的电磁辐射干扰问题,研究的对象为微波大功率雷达辐射对扩频通信系统微波频段内有用信号的干扰分析方法.
典型的雷达参数如表1所示[7].雷达对扩频通信系统的干扰分析可以分3步进行:
1)估计雷达干扰下扩频通信系统接收机前端的信干比;
2)分析雷达脉冲信号在接收机内部的干扰机理;
3)推导出扩频通信系统误码率计算公式.

表1 微波频段内典型雷达参数(2700~2900MHz)
1.1 接收机前端信干比的估算
扩频通信系统接收机在工作过程中,除接收到正常通信信号外,还可能受到地面、空中以及气象雷达信号的电磁干扰,在接收机前端,有用信号功率(单位:dBm)可表示为
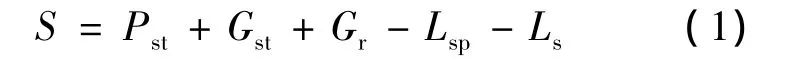
式中,Pst为信号发射功率,dBm;Gst为发射天线增益,dB;Gr为接收天线增益,dB;Lsp为信号空间传输损耗,dB;Ls为收发天线间的系统及插入损耗,dB.
接收干扰信号功率(单位:dBm)可表示为

式中,Pit为干扰信号发射功率,dBm;Git为干扰天线发射增益,dB;Lip为干扰信号空间传输损耗,dB.
视距条件下,空间传输损耗(单位:dB)[5]:

式中,r为收发相对距离,km;f为信号频率,MHz.其中FDR(Frequency Dependent Rejection)为频率相关抑制度,它由调谐抑制度(OTR,the On-Tune Rejection)和频率失谐抑制度(OFR,the Off-Frequency Rejection)两部分组成[8].BOTR为两系统工作时的带宽因子,且

BOFR为干扰发射机带宽与被干扰接收机带宽相重叠时的带宽因子,且
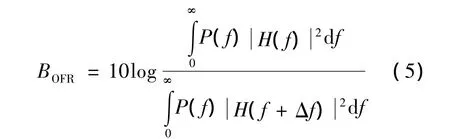
式中,Δf=fi-fr,fi和fr分别为干扰信号频率和接收机调谐带宽,同频干扰时,可取BOFR=0.
由式(1)、式(2)得接收机前端信干比(单位:dB):

1.2 雷达脉冲干扰机理分析
雷达发出的是一种周期性的梯形脉冲,具有脉冲上升时间tr、脉冲下降时间tf以及脉冲保持时间th,其时域波形如图1所示.为了分析方便,将梯形脉冲等效为与之能量相同、幅度相等的矩形脉冲[3],矩形脉冲宽度为
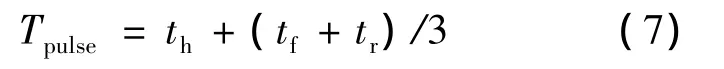
根据表1,假设 tr和 tf都为0.2μs,短脉冲保持时间 th为0.8μs,则等效矩形脉冲的宽度Tpulse=0.933≈1μs.长脉冲的等效矩形宽度可达几十微秒.
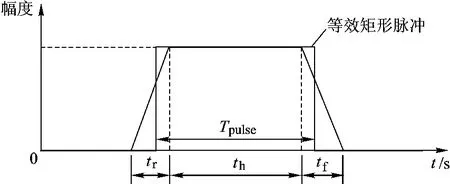
图1 梯形脉冲及其矩形脉冲等效图
扩频通信系统一般具有2的幂次方的扩频因子,切普速率通常达到兆比特每秒,以一种典型扩频通信系统的扩频码片速率6.5546Mbit/s为例,当扩频因子取32~1 024时,其信息符号周期为4.96~159μs,与雷达的脉冲长度可比拟,因此可以从时域上将雷达对扩频系统的干扰分为短脉冲干扰和长脉冲干扰分别进行讨论.
图2所示为短脉冲雷达对扩频通信系统干扰的时域图.由图中可以看出,当雷达脉冲远小于扩频通信系统符号周期时,一个雷达脉冲只会干扰到一个符号,个别的干扰到两个符号.设扩频接收机解扩前的带宽为Br,解扩后的中频带宽为Bm,信息符号长度为Ts,系统扩频处理增益为Sf,则实际进入扩频系统接收机的能量只有Tpulse/Ts,短雷达脉冲具有宽带频谱,经过解扩器后可认为获得处理增益Sf=Br/Bm,信噪比可表示为
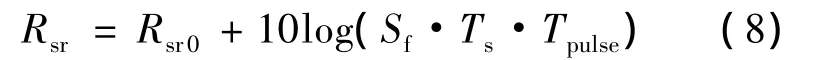
式中,Rsr0为接收机解扩器前信号功率与雷达峰值功率之比;Rsr为解扩后信号功率与雷达峰值功率之比.
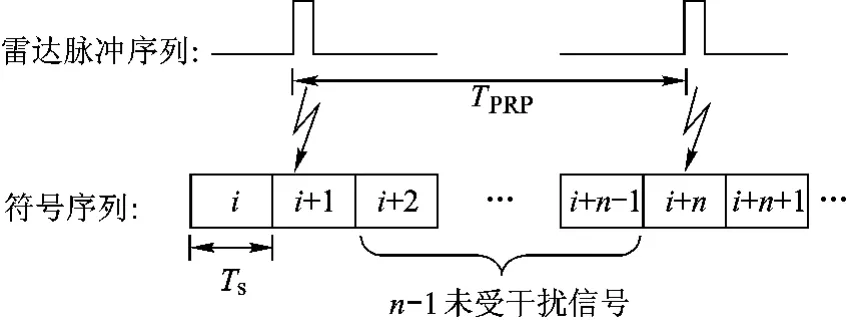
图2 短脉冲雷达干扰信息符号示意图
1.3 误码率公式的导出
假设扩频通信接收机基带采用QAM(Quadrature Amplitude Modulation)或QPSK(Quadrature Phase Shift Keying)相干解调,在只考虑雷达干扰的情况下,误码率[9]可表示为
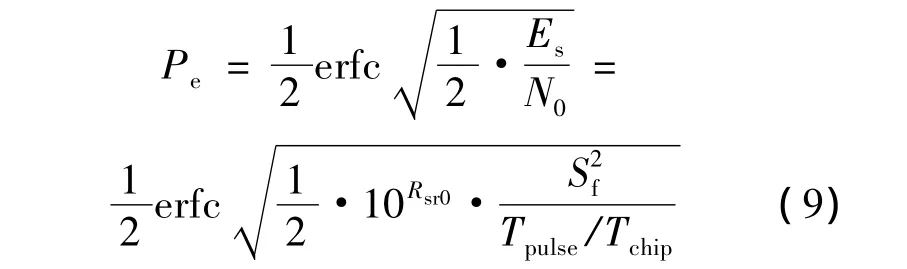
以上只考虑了扩频通信系统受到雷达脉冲干扰的那部分符号的误码率,相当于符号受到雷达脉冲干扰时的条件误码率,要得到总的误码率,还需考虑其它未受到雷达干扰的符号.由于短脉冲雷达与长脉冲雷达对系统符号造成的差错率有所不同,故分别考虑.
当雷达干扰为短脉冲时,一个雷达脉冲至多干扰到一个或两个信息符号,所以在一个雷达脉冲重复周期内,信息符号受到干扰的概率为信息符号周期Ts与雷达脉冲周期TPRP的比值,因而短脉冲雷达造成的总误码率可表示为
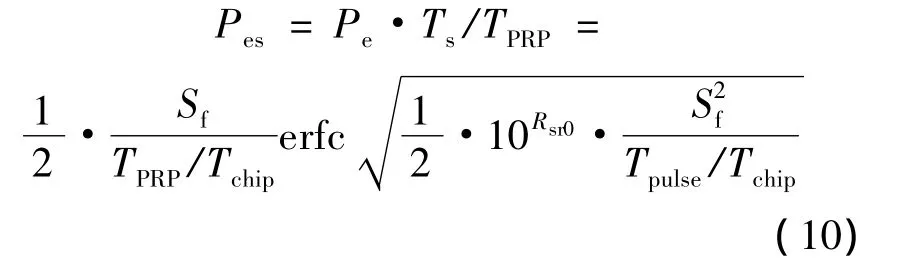
根据以上理论分析,结合表1中的雷达参数以及某型扩频通信系统技术指标,取短脉冲雷达Tpulse=1 μs,TPRP=1 ms,长脉冲雷达 Tpulse=100μs,TPRP=1 ms,扩频通信系统切普速率为6.5546Mbit/s,参变量扩频因子从 32 ~1 024,得到接收机分别受到短脉冲雷达和长脉冲雷达干扰时基带解调器输出端误码率与接收机前端信干比的对应关系曲线,如图3所示.
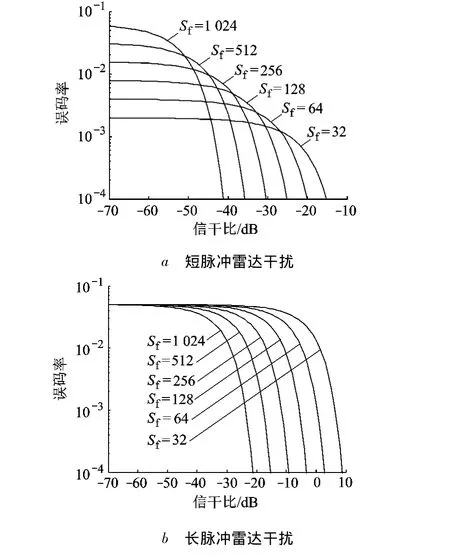
图3 雷达对扩频通信系统干扰误码率曲线
2 仿真研究
2.1 仿真模型设计
运用SIMULINK动态仿真工具、蒙特卡罗仿真方法以及“ode45”(4阶方法提供候选解,5阶方法控制误差)算法,遵循图4所示仿真工作流程,建立了扩频通信系统抗雷达干扰仿真模型,其中扩频通信系统为BPSK(Binary Phase Shift Keying)直接序列扩频调制体制,扩频码速率为6.5546Mbit/s,雷达脉冲重复周期为1ms,取样点数为105个.

图4 雷达对扩频通信系统干扰仿真流程图
2.2 仿真结果及分析
取扩频通信系统扩频因子Sf分别等于32~1024等6个2的幂次方,且模拟最坏情况即雷达与扩频通信系统同频时,雷达峰值功率对扩频通信系统的干扰过程,得到图5所示的误码率曲线.比较图3和图5知,短脉冲雷达干扰仿真误码率曲线与理论分析结果较为吻合,长脉冲雷达干扰仿真误码率在高扩频因子时比理论分析数值稍大,其主要原因是在实际扩频通信系统中,长脉冲雷达信号在经过中频滤波器后发生“脉冲展宽”效应,且在高扩频因子时,对于同一个信息码元,扩频码字更短,受干扰的码元增多,造成系统的误码率进一步加大.

图5 雷达对扩频通信同频干扰仿真误码率曲线
取Sf=128,由仿真模型得到雷达干扰下扩频接收机的误码率曲线如图6和图7所示.
图6表示长脉冲雷达和短脉冲雷达干扰下扩频接收机的信噪比-误码率曲线,可以看出,长脉冲雷达干扰对扩频通信的影响更为恶劣.
图7表示雷达与扩频通信系统载频间隔分别为5MHz和10MHz时的信干比-误码率曲线(Δf1表示短脉冲干扰情形,Δf2表示长脉冲干扰情形),可以看出,对于同一误码率指标,频率间隔越大,信干比的门限值越高.
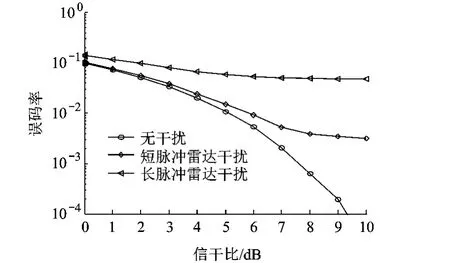
图6 不同雷达脉冲干扰下误码率曲线
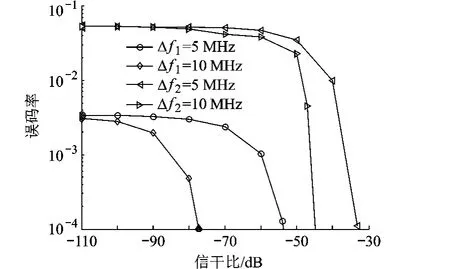
图7 雷达邻频干扰下误码率曲线
根据图5和图7的仿真结果,设扩频通信接收机灵敏度为-80 dB,取Sf=128,信道采用自由空间传播模型,考虑最恶劣的情况,即雷达发射信号获得主瓣增益并且始终对准扩频通信接收机,为保证通信接收误码率达到10-4以下,扩频通信系统与雷达的频率-距离间隔关系如表2所示.可以看出,当雷达与扩频通信系统的载频间隔为10MHz时,隔离距离为12.6 ~8310 km.
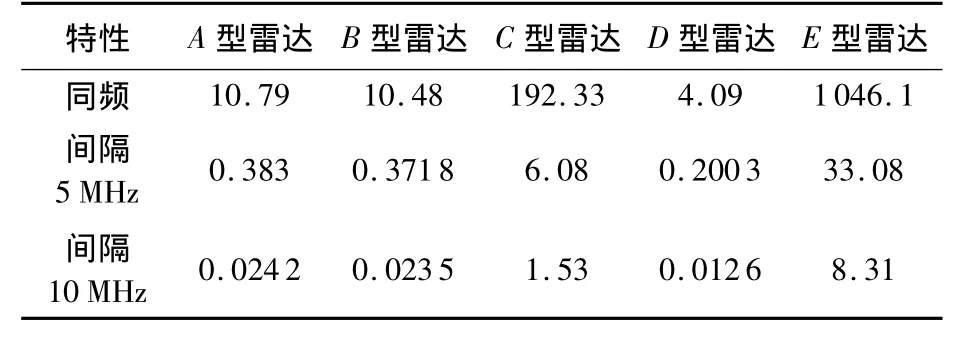
表2 雷达与扩频通信系统的频率-距离隔离关系 km
实际情形中,考虑到雷达天线的旋转效应以及扩频通信接收机一般包含硬限幅电路、前向纠错以及自动增益控制等纠错机制,可认为只要雷达的发射脉冲强度不会造成扩频通信接收机出现不可逆转的故障,则载频间隔10MHz以上时,雷达对扩频通信系统的影响较小.
3 结论
传统的雷达电磁辐射干扰分析,主要是基于检验受扰端口信干比大小从而判断设备对干扰是否敏感,这种静态的分析法固然能在干扰最坏情况下使系统满足性能要求,但也容易导致系统电磁兼容的过设计,降低了系统频谱利用效率.本文采用理论推导和仿真模拟两种方法,通过构建雷达对扩频通信系统在时域符号级上的干扰模型,分析得出了雷达峰值功率、脉冲长短、扩频系统的扩频因子等参数变化对雷达干扰效果的影响结果,较为深入地揭示了雷达对扩频通信系统的干扰机理,便于在实际中根据雷达的脉冲类型和扩频通信系统的技术指标进行相关频率协调和计算,从而使得对雷达电磁辐射干扰的分析更加微观化和合理化,有助于在确保雷达与其它电子信息系统之间电磁兼容的前提下,最大限度地提高频谱利用效率.当然,由于雷达的技术体制和天线工作方式多样,带外杂散辐射具有较强的不可预见性,因而雷达对扩频通信系统的干扰问题还需进一步深入研究.
References)
[1] Frost SW,Rigling B.Performance comparison for constrained radar waveform design[C]//Shannon Stiles.Proceedings of IEEE Radar Conference.Kansas city,MO,USA:IEEE Press,2011:724 -728
[2] Patton L K,Frost SW,Rigling B D.Efficient design of radar waveforms for optimized detection in coloured noise[J].IET Radar,Sonar& Navigation,2012,6:21 -29
[3] Deng X,Qiu C,Cao Z.Waveform design for enhanced detection of extended target in signal-dependent interference[J].IET Radar,Sonar& Navigation,2012,6:30 -38
[4] Zhao Bin,Kong Lingjiang,Mei Yang.A direct-path interference suppressing algorithm for shared-spectrum multistatic radar[C]//Wu Shunjun.Proceedings of2011 IEEE CIE international conference on radar.Chengdu,China:IEEE Press,2011:929 -932
[5] Xu Xiaojian,Chen Bing,Zhang Ping.Radar-communication integration based on DSSS techniques[C]//Zhou Mengqi.Proceedings of 8thInternational Conference on Signal Processing.Beijing:Chinese Acad of Sci,2006:1 - 4
[6] ITU-R Rec.M.1463-1 Characteristics of and protection criteria for radars operating in the radio determination service in the frequency band 1 215-1 400 MHz[S]
[7] ITU-R Rec.M.1461-1 Procedures for determining the potential for interference between radars operating in the radio-determination service and systems in other services[S]
[8] ITU-R Rec.M.1464-1 Characteristics of and protection criteria for radio-navigation and meteorological radars operating in the frequency band 2700-2900 MHz[S]
[9] ITU-R Rec.P.525-2 Calculation of free-space attenuation[S]
[10] ITU-R Rec.SM.337 Frequency and distance separation[S]
