在区试中应用Excel进行方差分析和多重比较

孙 伟

(黄冈市农业科学院，湖北黄冈438000)

在解决农业生产实际问题而进行的农业科学研究中，田间试验分析占有重要和不可替代的地位［1］，在生产中有了大量的数据，首先要确保数据的准确性和可靠性，然后再通过各种统计处理方法才能准确地说明实际问题。目前，各种统计软件如SAS、SPSS、Excel函数、Excel加载宏等已广泛应用于数据处理的统计分析，其中Excel函数是一款简捷、易懂、直观、使用方便的表格式数据综合管理和分析系统。本文以2010年湖北省早稻品种区试B组中某点的数据为例，介绍在Excel 2003中利用函数快速简单地进行田间试验方差分析和多重比较，同时对分析结果作出判断与分析。

1 原始数据部分

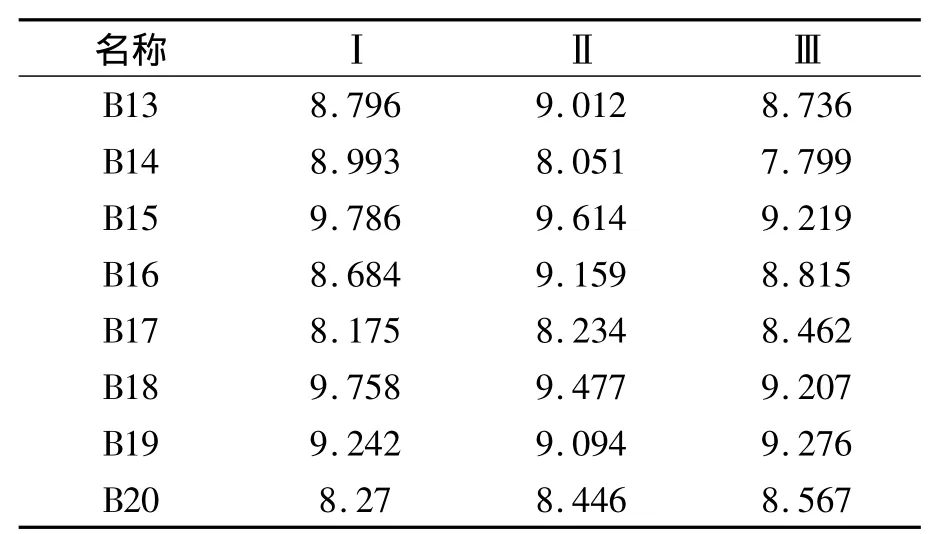
在这个例子中，按区试数据的要求，有11个品种(含对照)，设有三次重复，数值单位为(kg/0.02亩)，原始数据如表1。

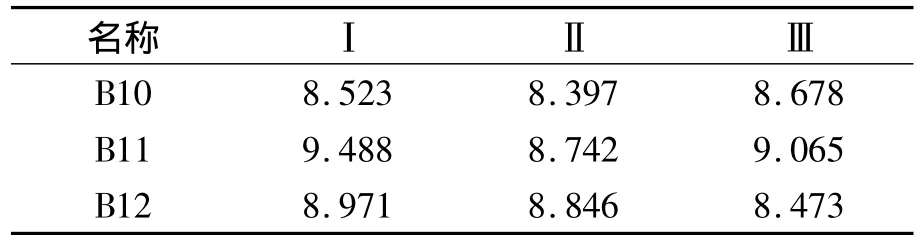
表1 2010年湖北省早稻品种区试B组产量表

?

2 数据分析

根据区试的规定和要求，在Excel中运用函数，计数count()、求和sum()、平均数average()、平方和sumsq()、条件函数IF()、引用函数index()等进行数据计算。计算数据(B3:G14)如图1。

图1 产量分析表

2.1 利用Excel计算平方和与自由度结果如图2

图2 平方和与自由度计算公式

2.1.1 计数

利用计数函数(count())计算出品种数和重复数:

n(重复数)=COUNT(B3:D3)=3

k(品种数)=COUNT(B3:B13)=11

T(各小区总数和)=SUM(B3:D13)=292.055

2.1.2 利用公式计算校正数:

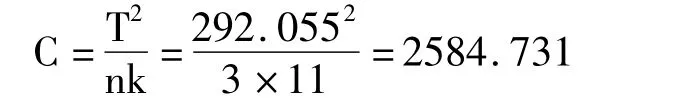
2.1.3 计算平方和

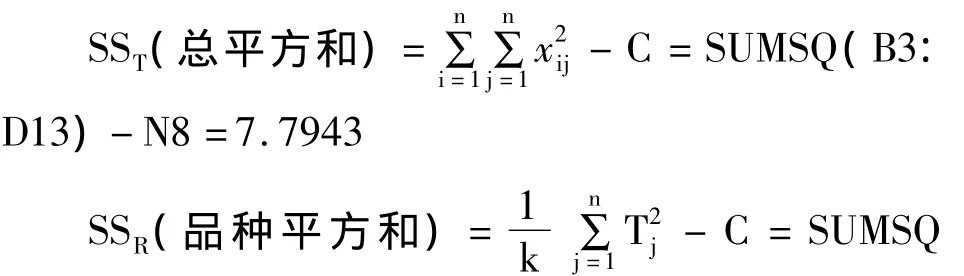
2.1.4 计算自由度

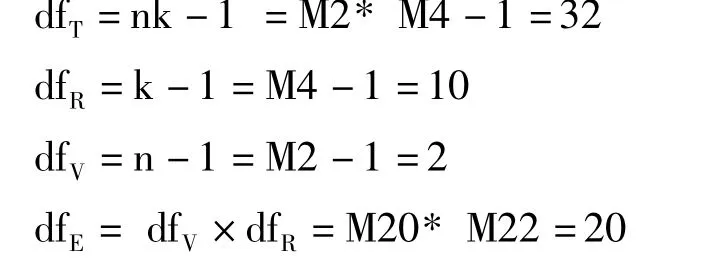
3 计算方差分析(如图3)

图3 方差分析结果

4 邓肯(Duncan)多重极差法(LSR法)

4.1 多重比较就是多个水平平均数间差异显著性测验，它的方法比较多，有LSD法(最小显著差数法)、LSR法(最小显著极差法)和改良的LSD法

对于LSD法和改良的LSD法，要查出相应误差自由度和显著水平下对应的t临界值，进而计算出最低显著差数LSD，与均数的差值相比。对于LSR法，要根据相应的误差自由度和不同的P(把所有平均数按大小顺序排序，进行差异显著性比较的两个平均数之间包括的平均数的个数)查出对应的t值，进而计算最低显著极差值LSR，与均数的差值相比。无论选择LSD还是LSR都涉及查表查出t值，但使用Excel中的TDIST函数就可以省略t值的查表，进行多重比较LSD法的计算。

4.2 最小显著差数法(LSD)

根据自由度求得的差异标准列成表如下:具体操作是分别在A34至 A43输入2至11，在SSR0.05下面即B34处输入(=INDEX(＇新复极差检验SSR值表p=0.05＇!$B$4:＇新复极差检验 SSR值表p=0.05＇!$T$49，Sheet1!$I$25，Sheet1!A34－1)(前提是新复极差检验SSR表值已输入到Excel中，并以此为表的名称))，同理在 SSR0.01下面即C34输入(=INDEX(＇新复极差检验SSR指标p=0.01＇!$B$3:＇新复极差检验SSR指标p=0.01＇!$T$47，Sheet1!$I$25 － 1，Sheet1!A 34－)，将标准差输入到D34列，再将对应的积放在 LSR0.05和 LSR0.01区间之中。(如图 4)

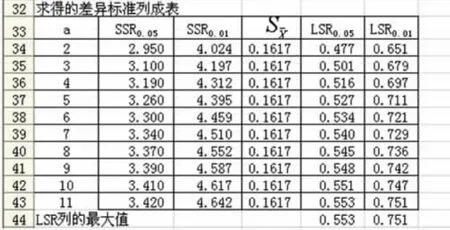
图4 LSR图表

4.3 差异比较

具体操作方法为:先将小区产量结果按大小降序排列，然后利用公式根据要求分别将两两之差填入对应的单元格中，(如C47中填入=IF(ABS(B$47－B48)＜B$47，ABS(B$47 －B48)，""))，然后在C48单元格中输入(=IF(C51＞E$44，IF(C51 ＞F$44，"＊ ＊"，"*")，""))来判断它们的差异(如图5)。

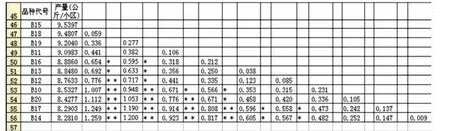
图5 梯形表

5 结论

从上面的分析可以看出，利用Excel软件进行试验数据的方差分析非常方便、快捷。尤其是其界面友好，易于操作。同时，利用其函数及排序等方法可以实现多个处理不同平均数间的多重比较，从而获得更多的科研试验信息，找出其中存在的规律。因此，在进行科研试验数据的方差分析及多重比较中，应用Excel表是可行的。这些方法有益于广大科研工作者处理科研数据，获得相关试验结果。那么，在一年一点和一年多点计算结合以上经验，再结合Excel中分类汇总等操作方法一样很方便地计算出结果。

［1］于永涛，刘成，吕玲等.玉米品种耐旱性评价及相关鉴定指标研究［J］.作物杂志，2008(04):55～58.