CFL加固受弯钢板中表面裂纹应力强度因子的数值分析*

张术宽 黄培彦 赵传宇

(1.华南理工大学土木与交通学院，广东广州510640;2.广州市特种承压设备检测研究院，广东广州510100; 3.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640)

表面裂纹是石油天然气管道、桥梁、海洋平台等钢结构中常见的、危险性最大的缺陷，在环境和载荷的反复耦合作用下表面裂纹会发生扩展，并致使结构失效，甚至会发生安全事故［1-3］.为了消除这种安全隐患，必须尽快对该类含缺陷的钢结构进行加固修复.在各类加固技术中，纤维增强复合材料(FRP)加固含缺陷钢结构的技术是近年发展起来的新技术，并得到了极大的关注［4-9］.采用FRP加固含表面裂纹状缺陷的钢结构后，在外载作用下该类加固构件的断裂机理研究对于其安全性和可靠性极其重要.为了探明其断裂机理，必须计算表面裂纹问题的应力强度因子(SIF)［10］.

对于半椭圆型三维表面裂纹的应力强度因子，由于没有解析解，一方面，长期以来其计算更多的是依赖于 Newman-Raju的半经验公式［11-12］;另一方面，随着计算机技术的发展和大型有限元软件的广泛应用，普通钢结构中表面裂纹问题的应力强度因子的有限元计算方法也得到了快速的发展［13-16］.然而，对于FRP加固钢结构中半椭圆型表面裂纹的应力强度因子的探讨还未见报道.为此，文中借助大型商用软件ANSYS，探讨建立半椭圆型表面裂纹的应力强度因子计算模型的方法，并对碳纤维薄板(CFL)［17］加固受弯钢板中的三维表面裂纹问题的应力强度因子进行数值分析.

1 三维表面裂纹SIF的有限元计算方法

三维表面裂纹问题应力强度因子有限元计算的核心问题是如何得到较高精度的计算结果.为此，需要建立适当的有限元计算模型，并对裂纹前缘附近区域的奇异单元进行正确的处理.为了达到上述目的，文中应用大型商用软件ANSYS，采用以下步骤和方法进行分析:(1)建立如图1所示的、计算弯曲载荷作用下未加固钢板中三维表面裂纹问题的SIF的有限元模型，得到该裂纹问题的SIF计算值;(2)利用Newman-Raju公式求得相应的理论值，并与有限元计算结果相比较，若两者吻合得很好，则认为有限元模型正确，否则，对有限元模型进行修正，直至两者的计算结果吻合得很好为止;(3)采用上述经过检验的模型和有限元算法，对CFL加固受弯钢板中的三维表面裂纹问题的 SIF进行数值分析.

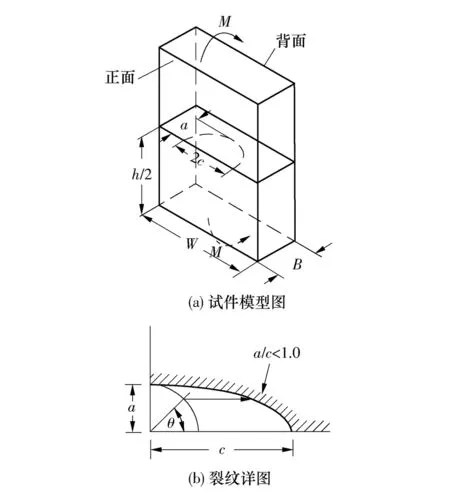
图1 弯曲载荷作用下的三维表面裂纹Fig.1 3D surface crack under bending load

本研究中，计算模型(试件)的固定计算参数为:弯矩M=27N·m，对应的弯曲正应力σb=100MPa，试件的宽度W=70 mm，高度h=92 mm，厚度B= 8mm;a/c为裂纹形状比，a/B为裂纹相对深度，θ是裂纹前缘椭圆的离心角.另外，定义裂纹开口的钢板表面为正面，相对的另外一面为背面.加固试件各组成材料的主要计算参数如表1所示.

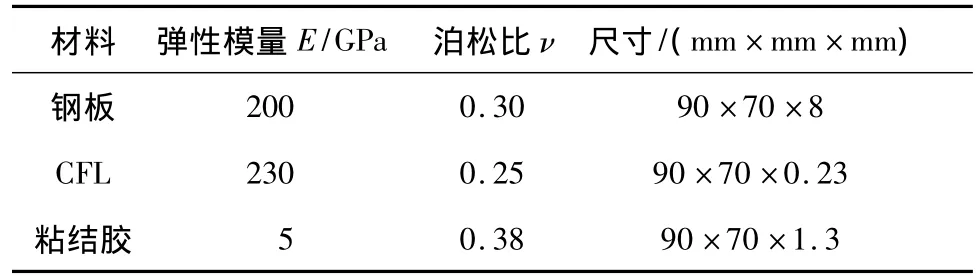
表1 各材料的主要参数Table 1 Main parameters of materials

1.1 有限元计算模型

1.1.1 奇异单元的生成

考虑到裂纹前缘的应力具有奇异性，ANSYS中用楔形(三棱柱形)1/4节点单元来解决裂纹前缘的SIF计算问题.在文中的计算模型中，奇异单元采用退化的Solid95单元，其它区域采用Solid45实体单元，如图2所示.

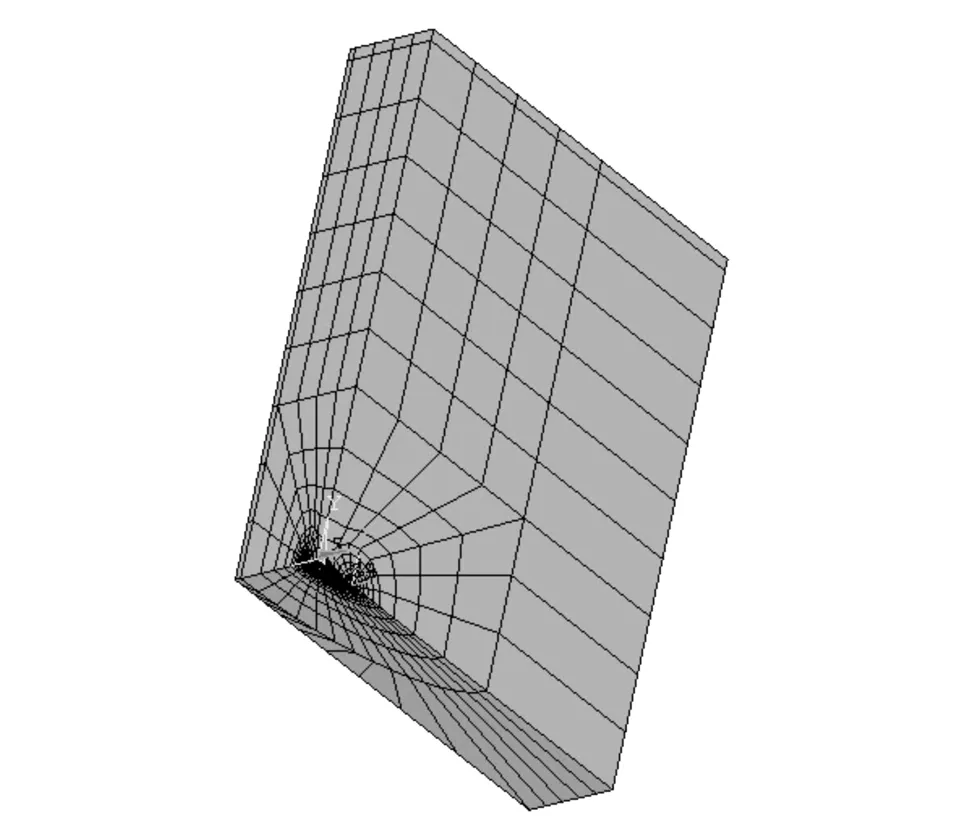
图2 未加固试件的有限元计算模型Fig.2 FE model of specimen without strengthening

按照ANSYS的技术文件要求，奇异单元在裂纹面上的边(径向边)应垂直于裂纹前缘，而退化的边(周向边)要沿着裂纹前缘的切向.为此，本研究利用ANSYS的lwplan命令建立了垂直于裂纹前沿的工作面，进而建立了符合上述要求的包围裂纹前沿的两层单元，即第一层单元为楔形的奇异单元(退化的Solid95单元)，中间节点置于边长的1/4处以获取应变的奇异性，如图3所示;第二层则为普通的六面体单元.

另外，为了得到合理的计算结果，按照ANSYS的技术文件要求，围绕裂纹尖端的第一层单元半径应小于或等于裂纹长度的1/8;在裂纹前缘方向，每个单元对应的中心角约为30°～40°.然而，建模的实践表明，这样的要求对二维裂纹比较适用，但不完全适用于三维表面裂纹.

1.1.2 裂纹前缘方向单元尺寸的确定

为讨论沿裂纹前沿方向单元边长对计算结果的影响，将椭圆型前缘曲线分别划分为10、20和30等份进行比较分析.当a×c=1.6 mm×3.2 mm时，应力强度因子KI的计算结果如图4所示.由图4可见，分为20等份和30等份时的计算结果几乎没有变化.即当裂纹前缘线被等分为20等份以上(对应的离心角变化值在5°以下)时，计算结果将趋于稳定.

图3 未加固试件中裂纹前缘的网格划分Fig.3 Meshes of crack front area of specimen without strengthening

图4 裂纹前缘方向单元尺寸对KI的影响Fig.4 Effect of element size in crack front direction on KI

1.1.3 径向单元尺寸的确定

一般来讲，单元网格划分越精细，计算结果越准确，但对于KI的计算，奇异单元过小会导致1/4节点的位移为零，从而无法计算KI.例如，当a×c= 1.6mm×3.2mm、θ=90°时，建立第一层奇异单元，对边长L1和裂纹半长c的比L1/c(单元径向尺寸)分别为1/17、1/22、1/40和1/58的模型进行计算，计算结果如表2所示.

由表2可知，当L1/c≥1/40时，有限元和Newman-Raju公式［11］的计算值基本吻合，但L1/c取1/58时，得到的计算结果明显不合理.经对比分析可知，L1/c不宜小于1/40.通过反复测试，发现L1/c的最佳值为1/15.

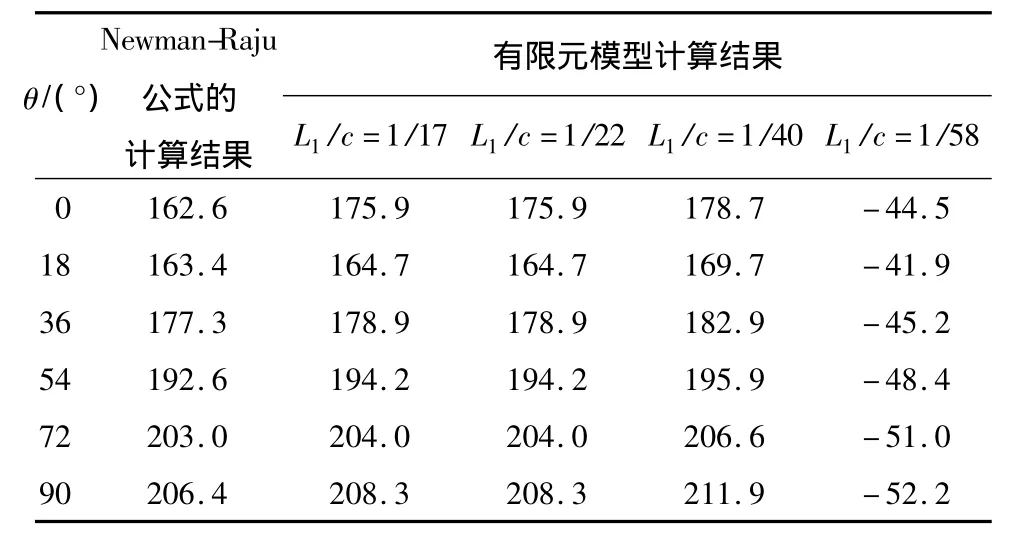
表2 单元径向尺寸对KI的影响Table 2 Effect of element size in radial direction on KI MPa·m1/2

1.2 模型测试

按上述方法确定单元尺寸并建立有限元模型，取裂纹尺寸为a×c=1.5mm×4mm(裂纹1)和a× c=2.68mm×4.47mm(裂纹2)进行计算，则两种裂纹的应力强度因子KI随椭圆离心角θ的变化曲线如图5所示.图5中，N-R表示由Newman-Raju公式得到的计算值，FE表示有限元模型计算值.

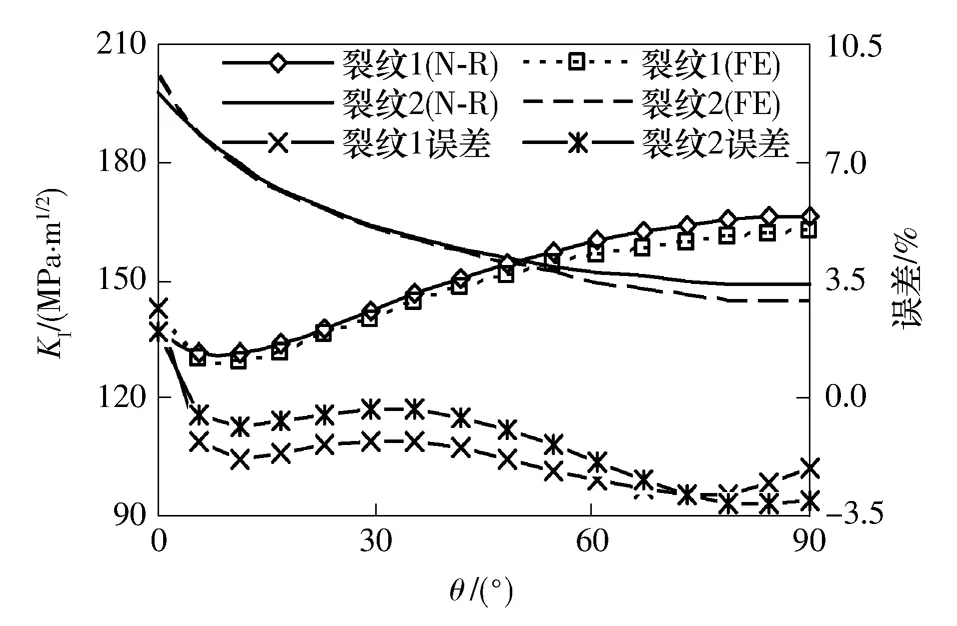
图5 KI的有限元和Newman-Raju公式计算结果的对比Fig.5 Comparison of computed values of KIobtained respectively by FEM and Newman-Raju equation

由图5可知，按文中方法建立的有限元模型的KI计算结果和Newman-Raju公式的计算值吻合得较好.其中，裂纹1的最大误差为2.64%，平均误差为1.70%;裂纹2的最大误差为3.07%，平均误差为1.30%.这表明采用上述方法建立的有限元模型是有效和可行的，它可以应用于FRP加固钢板中的三维表面裂纹问题的应力强度因子计算.

2 CFL加固钢板中表面裂纹SIF的有限元分析

为了对CFL加固钢板中的三维表面裂纹问题的SIF进行数值分析，需要按照前文所示方法建立有限元模型.为此，在图2所示有限元计算模型的基础上，于钢板的正面粘贴一层尺寸为90mm×70mm× 0.23mm的CFL予以加固，则加固后试件的有限元模型如图6所示.在该模型中，粘结胶层采用Solid45实体单元，CFL层采用Shell41单元，其余的与图2相同.加固件中裂纹前缘的网格划分如图7所示.利用该模型，可计算加固试件中三维表面裂纹的应力强度因子KI，并探讨其主要的影响因素.

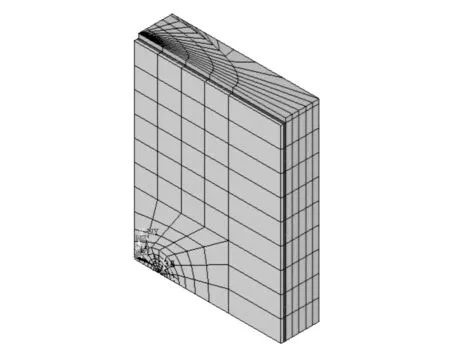
图6 加固件的有限元计算模型Fig.6 FE model of strengthened specimen

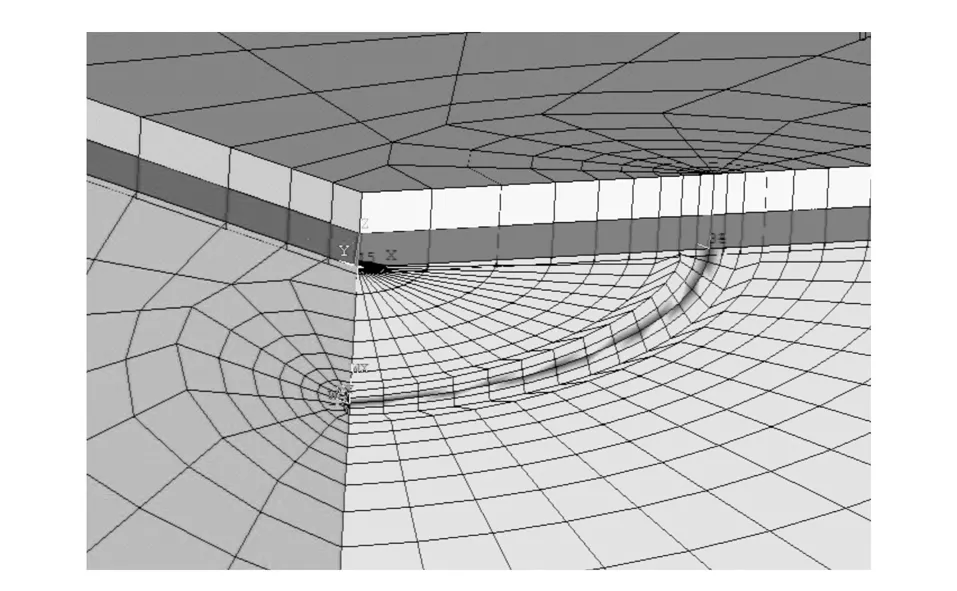
图7 加固件中裂纹前缘的网格划分Fig.7 Meshes of crack front area of strengthened specimen

为便于讨论各种因素对KI的影响，定义无量纲的应力强度因子RK为

式中，KIr为CFL加固后裂纹前缘某点的应力强度因子，KI则为加固前该点的应力强度因子.也就是说，RK越小加固效果越好.

2.1 CFL厚度对RK的影响

设a×c=1.5 mm×4 mm，θ分别为0°、30°、60°和90°时，由图6所示的模型可计算得到加固试件中三维表面裂纹的RK随着CFL厚度tf(mm)的变化曲线，如图8所示.

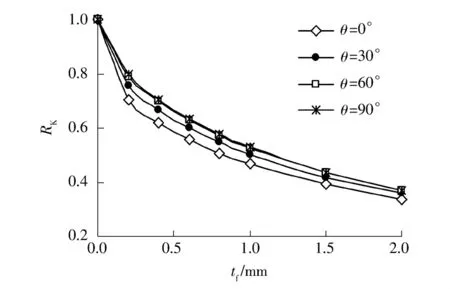
图8 CFL厚度对RK的影响Fig.8 Effect of CFL thickness on RK

由图8可知，裂纹不同位置的应力强度因子RK的变化趋势相似，都是随着CFL厚度的增加而降低.当CFL厚度小于0.4mm时，各点的RK值随厚度的增加迅速降低;但当CFL厚度大于0.4 mm时，RK降低速度减缓，大致与CFL的厚度呈线性关系.当tf=1.0mm时，与未加固试件相比，裂纹表面(θ= 0°)的KI可下降约54%，最深处(θ=90°)的KI可下降约48%.

根据有限元计算结果，θ=90°处(即表面裂纹最深处)的无量纲的应力强度因子RK与CFL厚度tf的关系式可表示为

由式(2)可知，如果通过对加固设计进行优化处理，则可以通过控制CFL材料用量而得到理想的加固效果.

2.2 裂纹形状比a/c对RK的影响

图9 在tf不同时裂纹形状比a/c对RK的影响Fig.9 Effect of crack shape ratio a/c on RKwith different tf

由图9可知，在相同加固条件下，裂纹形状比a/c=0.4的裂纹，加固前KI最大处在加固后的RK值大于其他两种形状比的裂纹.这是因为对于a/c= 0.4的裂纹，其加固前的最大SIF出现在裂纹的最深处，即θ=90°的位置;而对于其他两种裂纹，加固前的最大SIF出现在表面，即θ=0°的位置.在裂纹表面(θ=0°)，a/c=0.4的裂纹RK值则与其它两种裂纹相差不大(如图9中的表面点数值).这说明CFL加固对裂纹前缘上各点的约束作用随着裂纹深度的增加而减小.

上述规律可以在图10中更清楚地看到.当tf= 0.3mm，a/c分别为0.4、0.6、0.8时，裂纹前缘各位置上的RK值如图10所示.

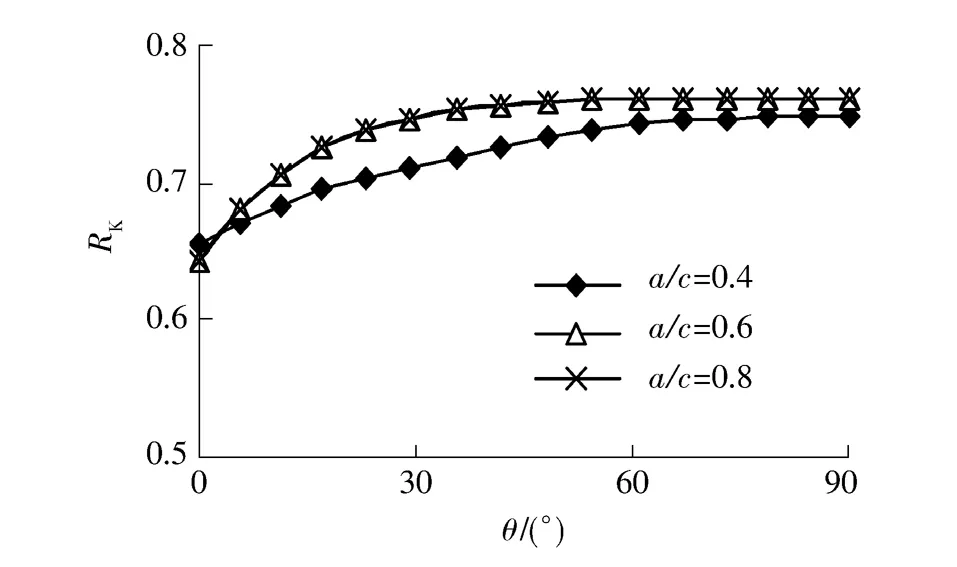
图10 面积为3 mm2时a/c对RK的影响Fig.10 Effect of a/c on RKwhen S=3 mm2

从图10可知，除了裂纹表面外，在加固试件的裂纹前缘的各个位置上，a/c=0.4的应力强度因子降低要比a/c为0.6和0.8的明显.

2.3 裂纹面积对RK的影响

tf=0.3mm，裂纹形状比a/c=0.4，0.6，0.8时、不同面积(S=3，6，9mm2)裂纹的无量纲应力强度因子RK随离心角θ变化的计算结果如图12所示.

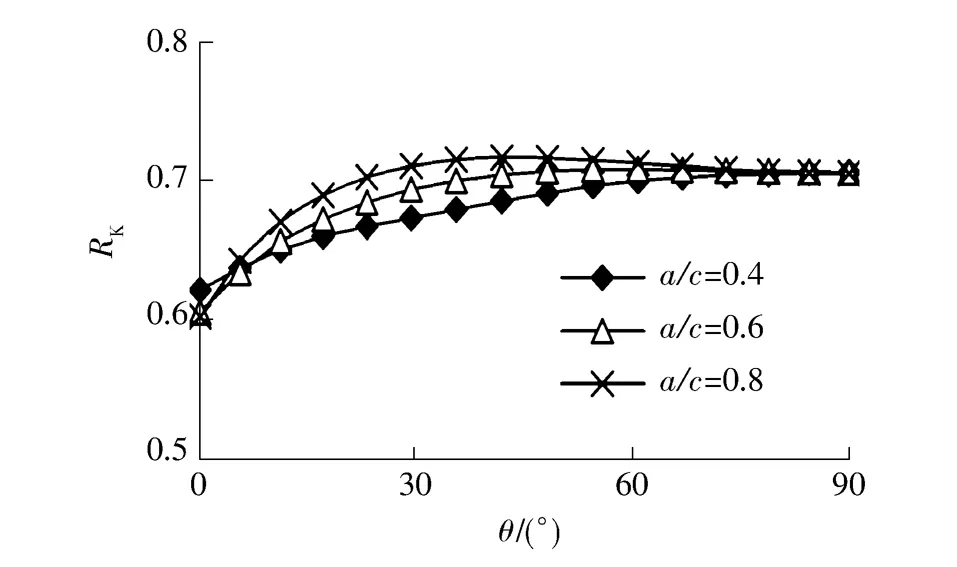
图11 面积为6 mm2时a/c对RK的影响Fig.11 Effect of a/c on RKwhen S=6 mm2

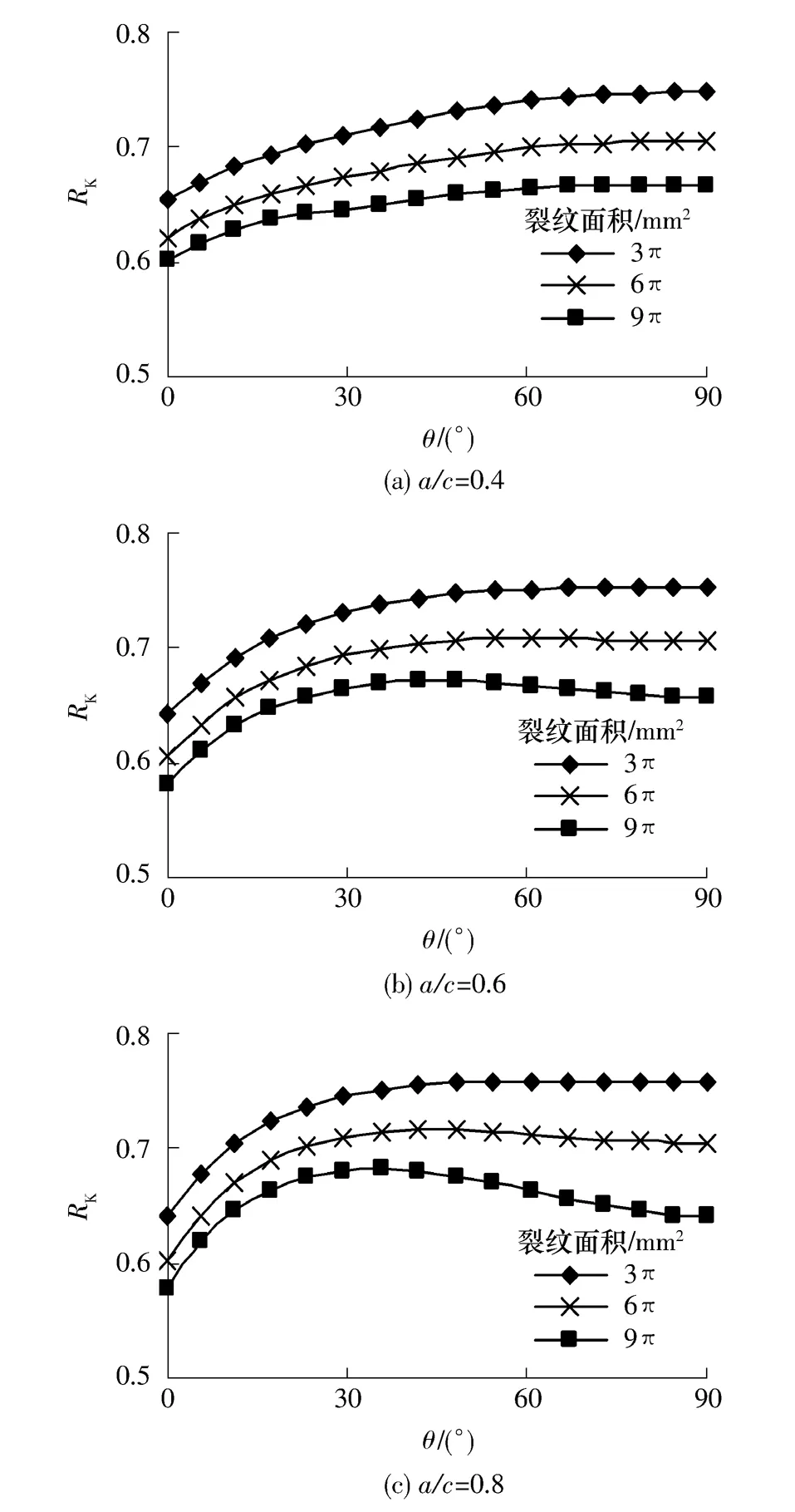
图12 裂纹面积对RK的影响Fig.12 Effect of cracking area on RK

由图12可知，不管裂纹形状比a/c如何变化，面积较大的表面裂纹被CFL加固后的RK较小，加固效果更显著.也就是说，构件的原缺陷越大加固效果越显著.这表明CFL加固含表面裂纹的受弯构件可以有效地抑制该裂纹的扩展.

3 结论

文中借助大型商用软件ANSYS，建立了半椭圆型三维表面裂纹的SIF计算模型，对模型进行了测试，并对CFL加固受弯钢板中三维表面裂纹问题的SIF进行了数值分析，讨论了各主要参数对SIF的影响，得到了如下主要结论:

(1)与Newman-Raju公式的比较表明，所建立的有限元模型是有效和可行的;

(2)CFL加固含裂纹的钢结构能够大幅度降低裂纹的SIF，有效抑制裂纹的扩展;

(3)加固件中裂纹的SIF降低速率随着CFL厚度的增加而变缓，为了提高加固效率，应对CFL的厚度进行优化设计;

(4)裂纹面积越大的表面裂纹，在CFL加固后其应力强度因子降低的幅度越大，加固效果越显著;

(5)对于细长浅裂纹(a/c较小)，CFL正面加固含表面裂纹的受弯钢板的效果更为显著.

［1］ Zhao Y，Roddis W M.Fatigue crack investigation for the Arkansas River Bridge in Hutchinson Kansas［J］.Construction and Building Materials，2000，14(5):287-295.

［2］ 赵在理.压力容器的结构分析与安全评估研究［D］.武汉:武汉理工大学能源与动力工程学院，2006.

［3］ 李亚宁，董保胜，赵新伟，等.含裂纹型缺陷压力容器用钢失效评定曲线研究［J］.有色金属，2007，59(1): 10-13. Li Ya-ning，Dong Bao-sheng，Zhao Xin-wei，et al.Investigation on failure assessment curves of pressure vessel steels with crack contained［J］.Nonferrous Metals，2007，59(1):10-13.

［4］ Jones R，Chiu W K.Composite repairs to cracks in thick metallic components［J］.Composite Structures，1999，44 (1):17-29.

［5］ Tavakkolizadeh M，Saadatmanesh H.Repair of damaged steel-concrete composite girders using carbon fiber reinforced polymer sheets［J］.Journal of Composites for Construction，2003，7(4):311-322.

［6］ Abdullah H，Klaiber F W，Wipf T J.Repair of steel composite beams with carbon fiber reinforced polymer plates［J］.Journal of Composites for Construction，2004，8(2): 163-172.

［7］ 郑云，叶列平，岳清瑞.CFRP加固疲劳损伤钢结构的断裂力学分析［J］.工业建筑，2005，35(10):79-82. Zheng Yun，Ye Lie-ping，Yue Qing-rui.Fracture mechanics analysis of steel structures with fatigue damages strengthened by FRP［J］.Industrial Construction，2005，35(10):79-82.

［8］ Deng J，Marcus M K，Stuart S J.Stress analysis of steel beams reinforced with a bonded CFRP plate［J］.Composite Structures，2004，65(2):205-215.

［9］ Karbhari V M，Shulley S B.Use of Composites for rehabilitation of steel structures-determination of bond durability［J］.Journal of Materials in Civil Engineering，1995，7 (4):239-245.

［10］ Zhang S K，Huang P Y，Zhao C Y.Numerical analysis of SIF of semi-elliptical surface crack on steel plate strengthened with CFL［J］.Chinese Journal of Solid Mechanics，2010，23(S):180-184.

［11］ Newman J C，Raju I S.An empirical stress-intensity factor equation for the surface crack［J］.Engineering Fracture Mechanics，1981，15(1/2):185-192.

［12］ ASTM E740—2003，Standard practice for fracture testing with surface-crack tension specimens［S］.

［13］ Sharobeam M H，Landes J D，.Numerical solutions for ductile fracture behavior of semi-elliptical surface crack［J］.Engineering Fracture Mechanics，1999，63(2): 131-145.

［14］ 周峰峦，高怡斐.半椭圆表面裂纹应力强度因子的有限元计算分析［J］.物理测试，2009，27(3):34-35，56. Zhou Feng-luan，Gao Yi-fei.Stress intensity factor of semi-elliptical surface cracks by finite element analysis［J］.Physics Examination and Testing，2009，27(3):34-35，56.

［15］ 刘青峰，谢基龙，缪龙秀.半椭圆表面裂纹的有限元仿真［J］.计算机辅助工程，2006，15(S):400-403. Liu Qing-feng，Xie Ji-long，Miao Long-xiu.Simulating semi-ellipse surface crack by finite element techniques［J］.Computer Aided Engineering，2006，15(S):400-403.

［16］ Hadi Khoramishad，Majid Reza Ayatollahi.Finite element analysis of a semi-elliptical external crack in a buried pipe［J］.Transactions of the Canadian Society for Mechanical Engineering，2009，33(3):399-409.

［17］ 黄培彦，曾竞成.纤维薄板及其应用:中国，ZL200410026742.8［P］.2006-08-23.