单层足尺砖混结构的拟动力试验及分析*

谭晓晶 吴斌

(哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090)

单层砌体结构是我国农村地区一种常见的建筑结构，其结构形式简单、造价低廉，被广泛应用于住宅、学校等建筑中.这种结构的抗震性能往往不被人们所重视，我国现行的抗震设计规范［1］仅针对多层砌体结构的设计，对于单层砌体结构的设计并未给予规定和指导.我国又是一个地震多发国，绝大多数地震发生在广大农村地区.因此，对单层砌体结构的抗震性能进行研究是很有必要的.

对单层砌体结构的抗震性能进行研究，抗震试验是一个非常有效的手段.常用的抗震试验技术有:拟静力试验、地震模拟振动台试验和拟动力试验.拟静力试验无法得到结构的地震反应，而地震模拟振动台试验由于受到台面尺寸和承载力的限制难以实现大型足尺模型试验;拟动力试验则弥补了两者的缺陷，既能再现结构地震反应全过程，又能进行大型足尺模型试验，从而避免了缩尺模型试验存在的尺寸效应，能真实反映结构的抗震性能.

对于砌体结构的抗震试验研究，文献［2-7］完成了带圈梁－构造柱墙片和砖房的拟静力试验和缩尺结构模型振动台试验.针对圈梁－构造柱抗震体系的恢复力模型、极限承载力、变形能力、抗震能力影响因素等做了大量工作;刘锡荟等［2］通过对带构造柱的墙片进行拟静力试验，提出了三折线恢复力模型和承载力计算公式;Tomaˇzeviˇc等［3］通过墙片拟静力试验给出了这种体系在极限状态下的承载力计算公式和相应的刚度计算公式;Bourzam等［5］通过试验研究得到了带构造柱墙片的刚度退化关系，并分别从砖墙承载力和构造柱效应方面分析了整个墙片的抗剪承载能力.相比较而言，对于足尺砌体结构模型试验的研究较少.Paquette等［8］完成了一个单开间无筋砌体足尺结构模型的拟动力试验，研究刚性砖墙与柔性木楼盖的相互作用以及木楼盖对结构地震反应的影响，但是试验模型没有设置构造柱; Kazemi等［9］通过一个单开间带构造柱足尺砖房模型的振动台试验，验证了抗震规范的合理性;San Bartolomé等［10］完成了一个两层足尺土坯房模型的振动台试验，发现增设构造柱能提高土坯房的抗震性能.上述试验对象多为缩尺结构模型和小型足尺结构模型，而对于大型足尺结构模型试验尚难以进行.

大型足尺结构模型试验通常需要更大的场地、更多的加载设备和经费，试验周期也更长，因而往往是一件比较困难的事情，目前尚未有人完成大型足尺单层砌体结构的拟动力试验.文中设计了一个足尺单层单开间砌体结构，在较小场地和较少经费投入的情况下，实现了大型足尺单层十开间砌体结构的全结构拟动力试验，并且定量确定了该类结构的抗震性能，阐述了大型足尺结构模型拟动力试验的实现方法，研究了带构造措施的单层砖房的抗震性能，以期为农村地区房屋的抗震设计提供参考.

1 试验方案

1.1 试验原理

原型结构为单层十个开间的砖混房屋，每个开间的尺寸均相同，仅取其中一个开间作为试验模型.结构的运动方程为

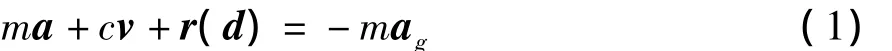
式中，m、c、r分别为原型结构的质量、阻尼系数和恢复力，a、v、d分别为原型结构的加速度、速度和位移，ag为地震动加速度.

原型结构中每片横墙所作用的恢复力可看作是相同的，那么结构总的恢复力可由试验模型恢复力的5.5倍来表示.结构的运动方程可表示为

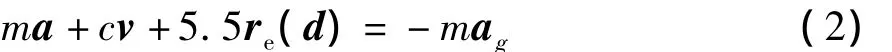
式中，re为试验模型所作用的恢复力.原型结构质量m为144.55t，实测总刚度为1213.1kN/mm，阻尼比取5%，时间步长为0.005s，采用中心差分法计算微分方程.中心差分法稳定性条件为

式中:ω为结构圆频率，经计算ω为91.61 rad/s;Δt为时间步长0.005s.显然，满足稳定性条件.

外部激励采用汶川地震什邡八角台站东西向加速度记录，截取了其中包括峰值段的35 s加速度时程.试验时不断增大峰值加速度，峰值加速度依次调整为0.8g、1.0g、1.2g、1.4g、1.6g和1.8g.

1.2 试验模型的设计与制作

试验模型的平面尺寸如图1所示，采用烧结普通砖和混合砂浆砌筑，砂浆配比为水泥∶石灰膏∶砂质量比1∶0.82∶13.4.纵横墙连接处砌成马牙槎，并沿墙高设置拉结筋，屋盖为钢筋混凝土整体现浇，结构构造措施如图2所示，结构材料特性见表1.

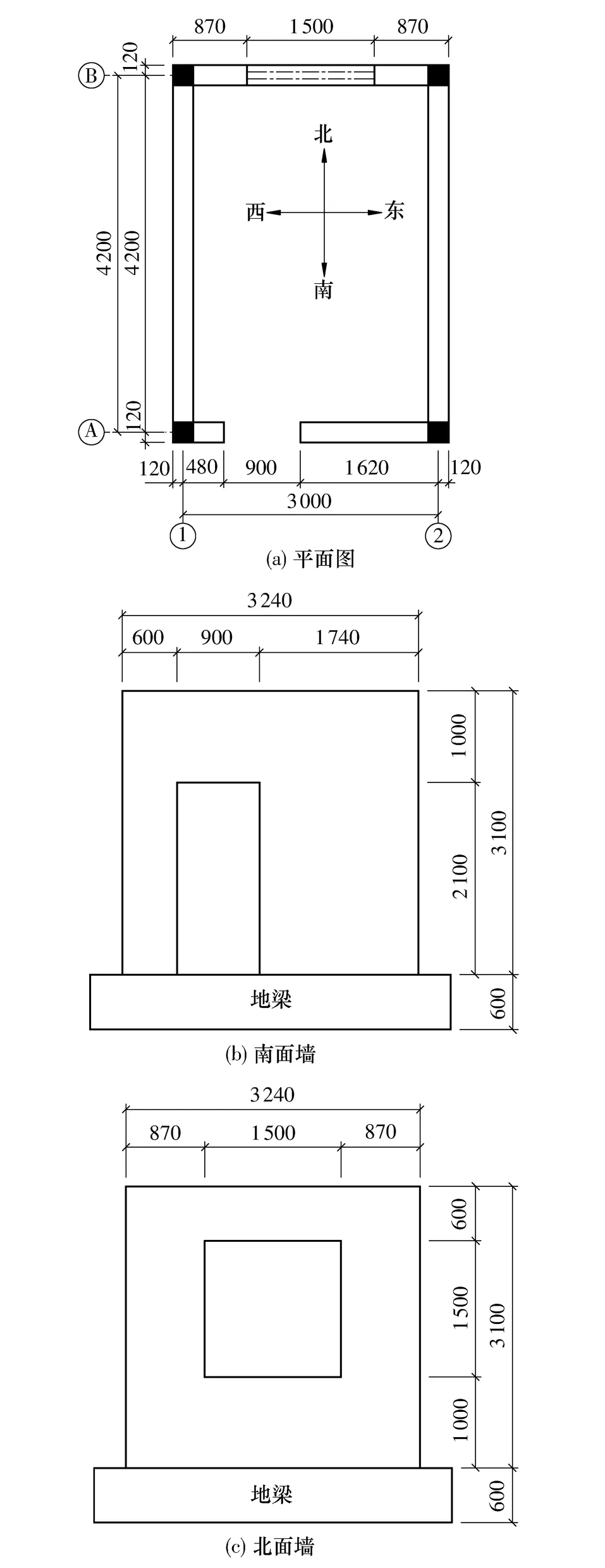
图1 试验模型尺寸(单位:mm)Fig.1 Dimensions of test model(Unit:mm)

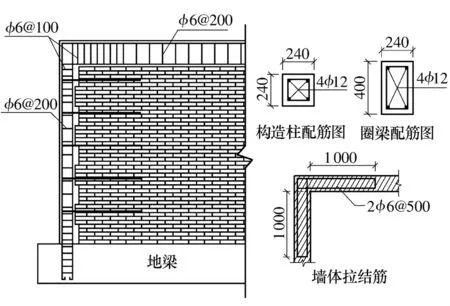
图2 试验模型构造措施图(单位:mm)Fig.2 Details of confinement of test model(Unit:mm)

2 试验结果及分析

2.1 结构破坏形态

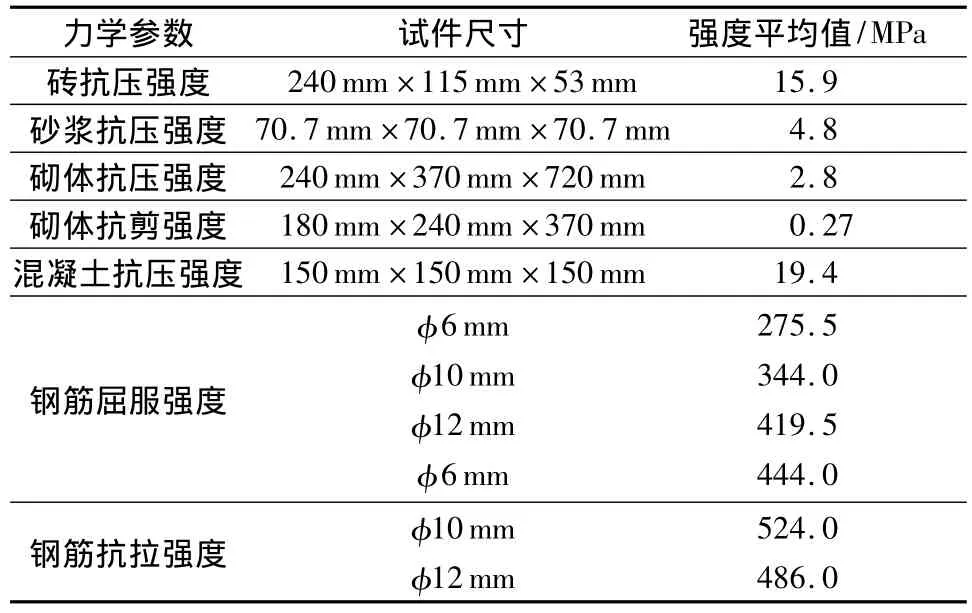
表1 试验模型材料力学特性Table 1 Material properties of test model

文献［11］阐述了结构的破坏形态.结构经历弹性、弹塑性和破坏3个阶段.地震动峰值加速度为0.8g至1.4g时，结构没有出现裂缝，基本处于弹性状态，构造柱和砖墙能很好地共同工作.随着地震动峰值加速度继续增大，结构底部所承受的倾覆力矩也增大.当峰值加速度增加至1.6 g时，受拉侧构造柱首先发生弯曲破坏，结构首先在西面墙的A轴构造柱下部出现水平向微裂缝，如图3(a)所示.当峰值加速度增加至1.8 g时，由于加载系统出现故障而仅完成了前10s的加速度时程加载.在这一加载过程中原有裂缝不断发展，西面墙墙体首先在中部发生由最大剪应力引起的水平裂缝，紧接着向墙体的左下角和右上角方向扩展，出现由主拉应力引起的沿灰缝呈阶梯状的斜裂缝，新的斜裂缝随即产生，东面墙也出现阶梯状斜裂缝(如图3(b)所示).墙体开裂后，构造柱受力增大，同时受到墙片的挤压作用，柱的顶部产生约为45°方向的剪切斜裂缝，同时在柱的中部处产生水平向弯曲裂缝.在这一阶段，位移和荷载关系开始呈现非线性，构造柱对已破坏的墙体起着约束作用.整个试验过程中，南、北墙体及屋面板均未见裂缝产生.

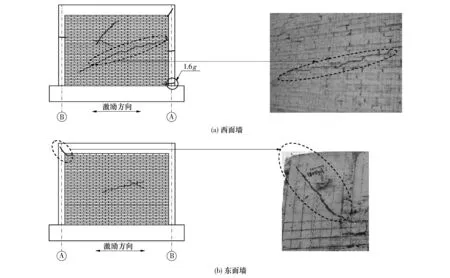
图3 试验模型的破坏形态Fig.3 Failure mode of test model

2.2 结构滞回曲线

峰值加速度分别为0.8、1.0、1.2、1.4和1.6 g时，试验模型的滞回曲线近似呈直线，结构位移反应很小，基本处于弹性状态.文献［11］给出了峰值加速度为1.6g、1.8g时的结构滞回曲线，如图4所示.

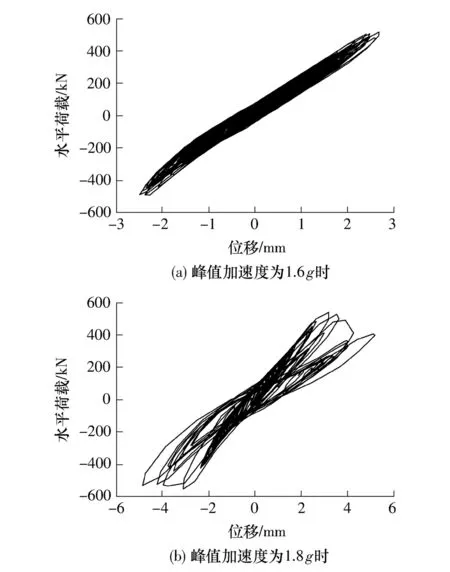
图4 结构滞回曲线Fig.4 Hysteresis loops of the structure

2.3 结构骨架曲线

把地震动峰值加速度为1.8 g时的滞回曲线水平荷载峰值点连接起来，得到结构的恢复力骨架曲线，可以近似用三折线来表示，如图5所示.由于未考虑结构纵墙平面外的承载能力，该骨架曲线忽略了纵墙上洞口的影响.骨架曲线上两个特征点为开裂点和极限点，开裂点前结构处于弹性状态，开裂点后骨架曲线刚度退化，结构变形增大，但荷载仍会上升.当达到极限点时，承载力和刚度都出现了退化现象，但荷载值并未急剧下降.开裂点至极限点过渡段比较短，屈服荷载接近极限荷载.

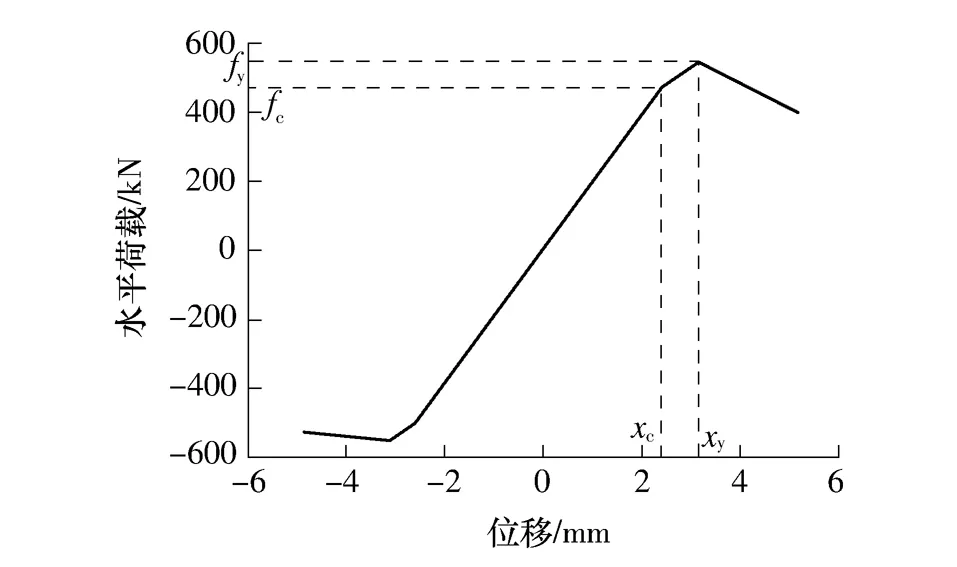
图5 结构骨架曲线Fig.5 Skeleton hysteresis curve of the structure

3 结构位移反应数值计算

结构的地震反应采用单自由度剪切层模型来计算，其恢复力则采用刚度退化的三折线模型.恢复力模型的骨架曲线特征点参数可采用文献［2］中提出的公式计算.计算得到结构的初始刚度 k1为460.90kN/mm，第二刚度k2为73.74 kN/mm，第三刚度k3为－73.74kN/mm，开裂位移xc为1.1mm，极限荷载位移xy为2.4 mm.在完成全部试验工况之前，结构已经经历了多次加载测试，每次测试都会对结构造成一定的损伤，造成结构刚度衰减.第一次测试结构的初始刚度为547.52kN/mm，最后一个试验工况测试得到结构的特征点参数如表2所示.

表2 恢复力模型参数值Table 2 Parameters values of hysteretic model

由表2可以看出，按文献［2］计算得到的结构初始刚度小于第一次测试前的实测刚度，而经过多次试验后，结构的刚度衰减很严重.结构的地震反应数值计算将采用最后一个试验工况测试得到的结果.恢复力模型的滞回规则如图6所示.

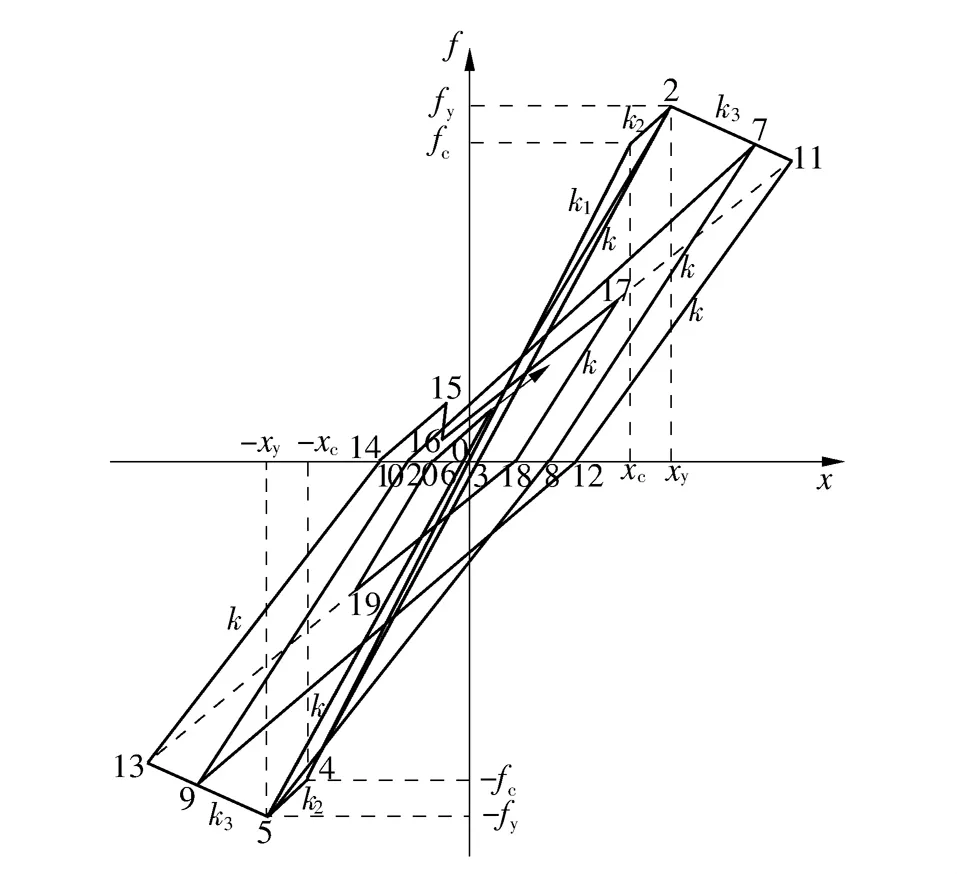
图6 结构恢复力模型Fig.6 Hysteretic model of the structure

点1和4为开裂点，相应的力与变形分别为fc、xc和－fc、－xc，线0-1与线0-4为弹性段，刚度均为k1;点2和5为极限点，相应的力与变形分别为fy、xy和－fy、－xy，线1-2和线4-5的刚度为第二刚度k2;线2-11和线5-13为刚度下降段，刚度为第三刚度k3.弹性段后每完成一次循环加载，均考虑结构的残余变形和刚度退化，卸载刚度k按文献［2］中的公式计算.该模型认为:卸载刚度与卸载时结构的变形有关，反向加载时直线指向前一次循环的最大变形处.图6中第一次加载循环后结构处于点6状态，再正向加载时，结构指向上次循环的最大变形处点2，卸载时沿线7-8，在点8反向加载，指向前次最大变形处点5，反向卸载时沿着线9-10到达点10完成了第二次循环加载.第三次循环加载从点10指向点7，卸载时沿线11-12，在点12反向加载，指向前次最大变形处点9，反向卸载时沿着线13-14完成第三次循环加载.第四次循环加载从点14指向点11，若中途出现卸载，则沿线15-16，再次正向加载则沿线16-11，中途再次卸载则沿线17-18，从点18沿线18-13反向加载，中途反向卸载沿线19-20，后续循环加载从点20指向点11按同样规则进行.文献［12］也采用三折线恢复力模型，但滞回规则没有考虑卸载时的残余变形和刚度退化.

利用Matlab编制结构动力时程分析程序进行结构位移反应计算，并与试验结果进行对比，如图7所示.

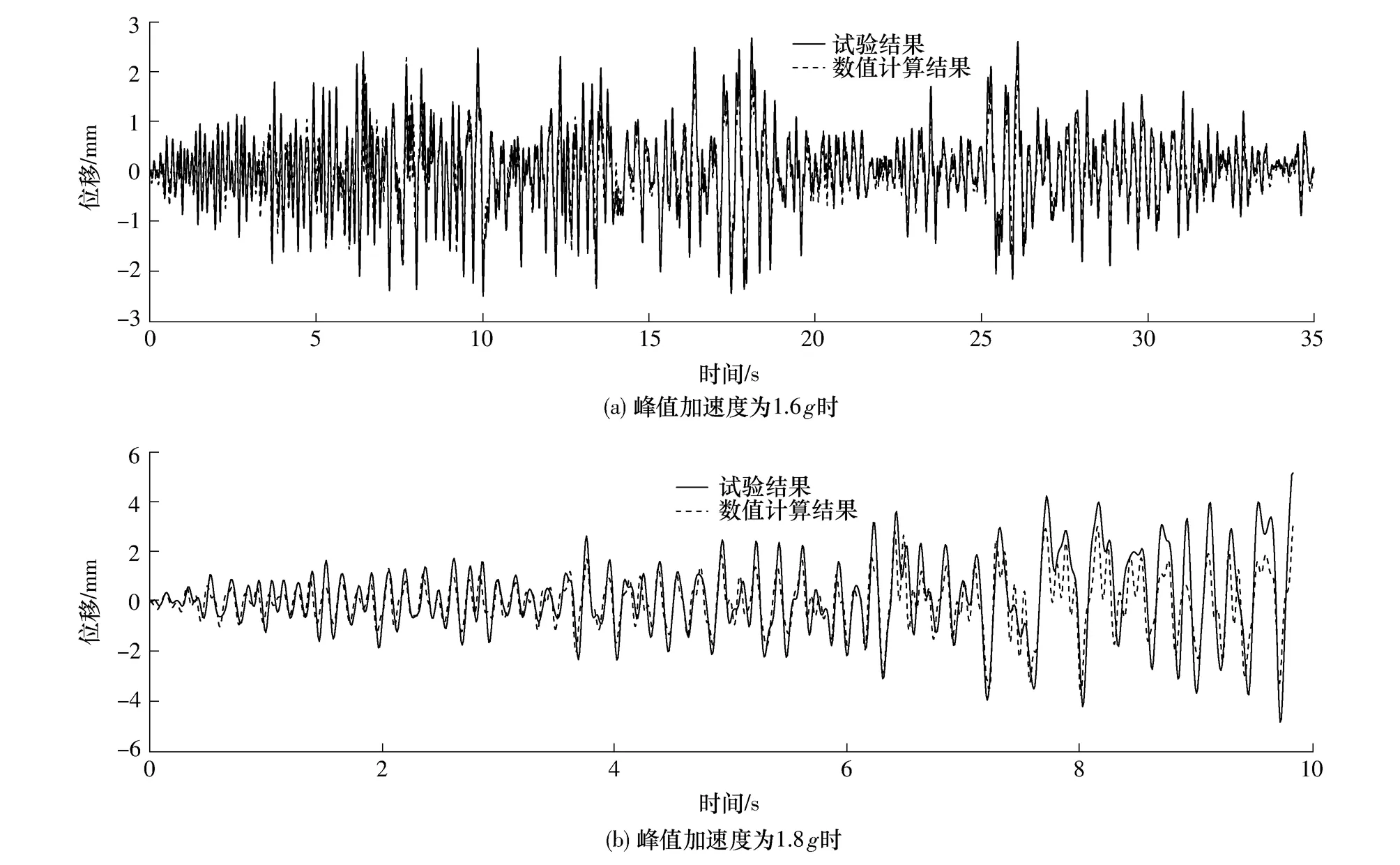
图7 不同地震动峰值加速度激励下结构的位移反应Fig.7 Displacement response of test model under different peak ground acceleration excitations

从图7中可以看出，试验与计算得到的位移反应趋势大致相同.地震动加速度峰值为1600gal时，结构基本处于弹性阶段，计算结果与试验结果比较接近.地震动加速度峰值为1800 gal的前10 s，结构由弹性状态逐渐进入弹塑性状态;当结构处于弹性状态时，试验与计算结果吻合得较好，而当结构进入弹塑性状态后，数值计算结果与试验结果偏离较大，计算结果峰值要比试验结果峰值小36%左右;倘若试验完成全部35s，结构的刚度将继续退化，而程序中不能精确体现这一退化规律，那么两者的误差将更大，计算得到的峰值将更小于试验结果.由此，对于砌体结构的弹塑性地震反应数值分析，恢复力模型滞回规则的精确程度很重要.可在三折线恢复力模型基础上，对滞回规则作进一步改进，以便能更精确地模拟结构的地震反应.

4 结构承载能力计算

结构的承载力计算一般要考虑砖墙承载力和构造柱承载力的共同贡献.刘锡荟等［2］提出了墙体开裂荷载和极限荷载的计算公式，开裂荷载计算考虑了把构造柱折算为砖墙体的总抗剪能力，极限荷载计算则考虑了砖墙体的摩擦抗剪效应与构造柱钢筋的销键作用.邬瑞峰等［6］提出了工程用的极限承载力计算简化公式，该公式把墙体的承载力分为3部分:砖墙体的抗剪能力、砖的摩擦力和构造柱的抗侧能力，但并没有提出相应的开裂荷载计算式.Tomaˇzeviˇc等［3］用一个折减系数乘以砖墙的抗剪能力，用来计算墙体的开裂荷载，该系数一般取为0.7～0.8;墙体的极限荷载计算则同时考虑了砖墙体的抗剪能力和构造柱钢筋的销键作用.而Bourzam等［5］也采用相同的思路，提出的折减系数为0.6～0.8.表3为依据各理论公式计算得到的结构承载力，各公式中的材料强度均取为平均值.结构承载力试验结果取为正反方向的平均值，开裂荷载为489.70kN，极限荷载为547.20kN.未设置构造措施结构的极限承载力为各计算公式减去构造柱的贡献部分，但其开裂荷载并未提出相应的计算方法.

表3 结构承载力计算结果1)Table 3 Calculated bearing capacity of the structure

从表3可以看出，由各公式计算得到的设置了构造措施结构的极限承载力均接近试验值，其中文献［2］提出的公式的计算值最大，且其值大于试验值，其余计算值均小于试验结果，而以文献［3］提出的公式的计算值最小.在未设置构造措施结构的承载力中，文献［5］的方法的计算值最大，这是因为在Bourzam等提出的公式中，当墙体高宽比小于1时，剪力不均匀系数为1，而其余公式均为1.2.从设置与未设置构造措施结构的极限承载力对比可以看出，设置构造措施后，结构的极限承载力提高了20%～50%，这说明圈梁构造柱体系是一种有效的抗震措施.

规范［1，13］中提出了截面抗震承载力计算公式，采用材料强度设计值并考虑抗震调整系数计算得到的结构承载力为208.38kN，而采用材料强度平均值且不考虑抗震调整系数计算得到的结构抗震承载力为460.34kN.由规范计算得到的结构承载力小于试验结果，计算公式是偏于安全的，对结构抗震设计是有利的.

5 结论

通过对设置了构造措施的单层足尺砖混结构进行拟动力试验和抗震性能分析，得到如下结论:

(1)通过设计小型足尺单层单开间结构模型，可以很好地完成大型足尺单层多开间结构的全结构拟动力试验，从而节省试验成本.

(2)试验中的该类单层砌体结构具有很强的抗震性能，具有抵御地震峰值加速度为1.6 g的地震作用的潜力.

(3)当结构进入弹塑性状态时，三折线恢复力模型的滞回规则尚不能精确描述结构刚度的退化规律，需要作进一步改进以便能更精确地模拟结构的地震反应.

(4)采用现有的一些理论公式计算的结构极限承载力接近试验结果，在实际工程计算中，这些公式可作为一种很好的参考.规范中的计算公式偏于安全，对抗震是有利的.

(5)设置圈梁构造柱的结构承载力比未设置圈梁构造柱的结构承载力提高了20%～50%，拟动力试验结果也再次验证了设置这种构造措施的单层结构在大震下具备很高的安全储备，表明圈梁构造柱体系是一种有效的抗震措施.

［1］ GB 50011—2010，建筑抗震设计规范［S］.

［2］ 刘锡荟，张鸿熙，刘经纬，等.用钢筋混凝土构造柱加强砖房抗震性能的研究［J］.建筑结构学报，1981，2 (6):47-55.Liu Xi-hui，Zhang Hong-xi，Liu Jing-wei，et al.A study of aseismic characteristics of masonry building with reinforced concrete tie-columns［J］.Building Structures，1981，2(6):47-55.

［3］ Tomaˇzeviˇc M，Klemenc Iztok.Seismic behavior of confined masonry walls［J］.Earthquake Engineering and Structural Dynamics，1997，26(10):1059-1071.

［4］ Kenneth A Gent Franch，Gian M Giuliano Morbelli，Maximiliano A Astroza Inostroza，et al.A seismic vulnerability index for confined masonry shear wall buildings and a relationship with the damage［J］.Engineering Structures，2008，30(10):2605-2612.

［5］ Bourzam Abdelkrim，Goto Tetsuro，Miyajima Masakatsu.Shear capacity prediction of confined masonry walls subjected to cyclic lateral loading［J］.Structural Eng.Earthquake Eng，2008，25(2):692-704.

［6］ 邬瑞锋，吕和祥，奚肖凤.具有构造柱墙体弹塑性、开裂、裂缝开展的分析［J］.大连工学院学报，1979，18 (1):60-72.Wu Rui-feng，Lü He-xiang，Xi Xiao-feng.Elasto-plastic analysis and crack growth analysis of reinforced masonry shear wall［J］.Journal of Dalian University of Technology，1979，18(1):60-72.

［7］ 夏敬谦，黄泉生.构造柱与配筋砌体房屋抗震能力的试验研究［J］.地震工程与工程振动，1989，9(2):82-96.Xia Jing-qian，Huang Quan-sheng.Model test of brick masonry building strengthened with rc tie columns［J］.Earthquake Engineering and Engineering Vibration，1989， 9(2):82-96.

［8］ Paquette Jocelyn，Bruneau Michel.Pseudo-dynamic testing of unreinforced masonry building with flexible diaphragm and comparison with existing procedures［J］.Construction and Building Materials，2006，20(4):220-228.

［9］ Kazemi M T，Hoseinzadeh Asl M，Bakhshi A，et al.Shaking table study of a full-scale single storey confined brick masonry building［J］.Transaction A:Civil Engineering，2010，17(3):184-193.

［10］ San Bartolomé A，Delgado E，Quiun D.Seismic behavior of a two story model of confined adobe masonry［C］∥Wael W.El-Dakhakhni，Robert G.Drysdale.Proceedings 11th Canadian Masonry Symposium.Toronto:McMaster University，2009.

［11］ 谭晓晶，吴斌.砖混结构足尺模型的子结构拟动力试验［C］∥土木工程结构试验研究及教学最新进展.上海:同济大学出版社，2011:190-194.

［12］ 李志鹏.隔震砌体结构的抗震性能分析［D］.哈尔滨:哈尔滨工业大学土木工程学院，2009.

［13］ GB 50003—2001，砌体结构设计规范［S］.