基于数值模拟的空调末端节能优化*

闫军威 刘洋 周璇 康英姿

(华南理工大学机械与汽车工程学院，广东广州510640)

随着近年来公共建筑的日益增多，公共建筑所带来的能耗问题也引起了各方面的重视，据统计，我国大型公共建筑总能耗占全国城镇总耗电量的22%，其单位面积年耗电量达到100～300kW·h［1］.空调系统的能耗在公共建筑总能耗中占了40% ～60%［2］，而空调末端能耗占中央空调总能耗的20%～30%.末端能耗过高主要是由于空调末端设备按最不利工况设计，其额定工况下的制冷能力绝大部分时间远大于房间实际冷量需求.空调末端设备的运行参数往往被设定为最大，使得空调房间存在着温度过低的现象.这样，不但室内的热舒适性较差，而且过多的冷量也造成了能源的浪费.因此，在满足空调房间舒适性的前提下，研究空调末端设备节能运行参数，对于末端设备节能具有重要意义.

利用计算流体力学(CFD)软件进行数值模拟方法具有省时、成本低、结果可视化等特点，广泛应用于室内气流组织分析、室内环境热舒适性分析等领域，国内外已有许多学者利用CFD技术对室内的热舒适性开展了研究.陈曦［3］通过CFD技术模拟了某办公室在冬季空调供热时的热舒适性和细菌的传播.薛若军等［4］通过CFD技术确定了某空调供冷房间的热舒适性程度.但是，利用CFD技术在保证室内热舒适性的前提下，确定室内送风参数以达到空调房间末端节能的研究并不多.

文中利用暖通空调领域广泛采用的AIRPAK3.0数值模拟软件，分析了送风参数对典型办公房间室内温度场和速度场分布的影响，并结合软件中的热舒适性模块分析了不同的送风参数对室内热舒适性的影响程度;在满足房间热舒适性的前提下，研究了办公建筑空调末端设备的最佳送风参数;同时，将优化后的末端工况与一天内实际运行工况进行了对比.

1 边界条件和模型的建立

1.1 物理模型

1.1.1 模型尺寸和热工参数的确定

实验时间为8月下旬某日，当日天气晴朗，所研究的办公室位于广州大学城某高校一办公楼四层，外窗朝东，南北两侧房间均为空调供冷区域，办公楼整体为砖混结构，外墙表面有浅色饰面砖，东向无高大建筑遮挡.房间尺寸为7.78m×5.4m×2.6m，忽略外墙外表面空气流速变化对外墙传热系数的影响，笔者估算围护结构的传热系数为1.53W/(m2·K)［5］，天花和地面近似为绝热.

室内热源、墙体及外窗尺寸如表1和2所示.

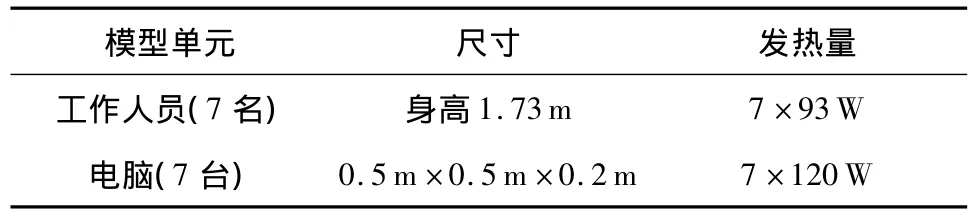
表1 室内热源Table 1 Indoor heat source

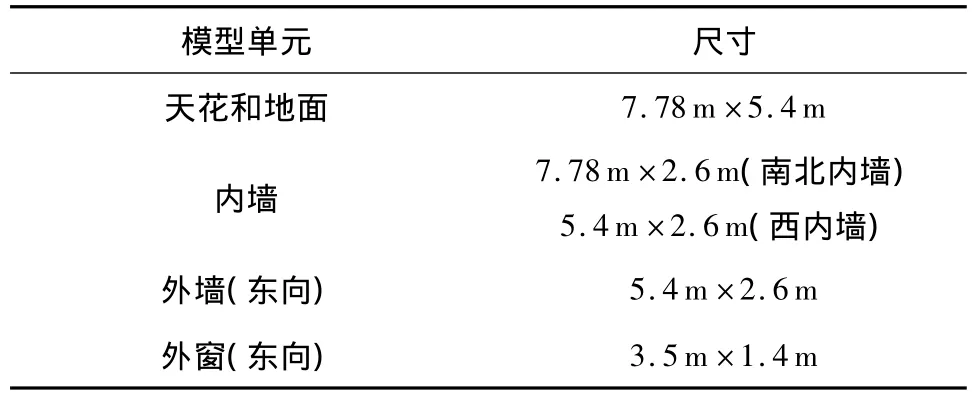
表2 墙体和外窗尺寸Table 2 Size of walls and window

由于风口模型对室内气流组织的模拟结果具有较大的影响，送风口模型采用文献［6］中的方形散流器九点风口模型［6］，将送风口分为9个部分，并分别设定各部分的速度矢量值.实验结果发现，选择该模型的计算结果与实际的入口边界条件较接近［7］.模型的等效图如图1所示，建立好的模型如图2所示.

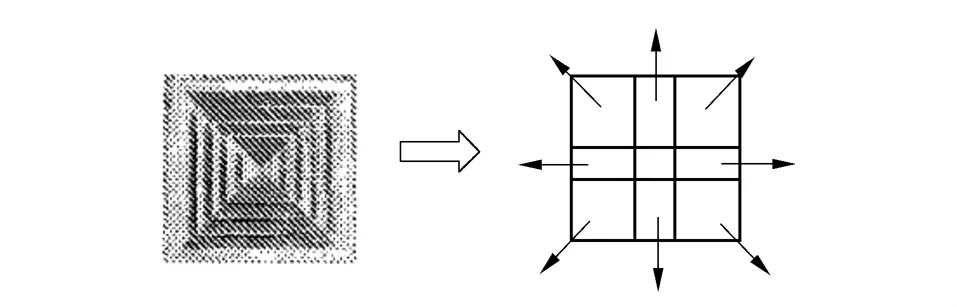
图1 方形散流器九点风口模型Fig.1 9-point supply opening model of square diffuser

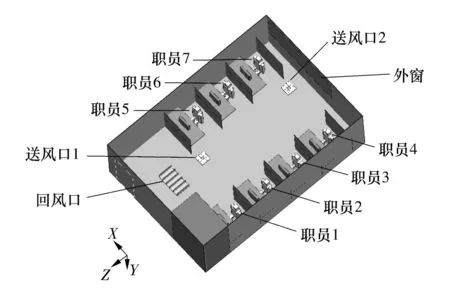
图2 办公室的几何模型Fig.2 Geometric model of the office

1.1.2 太阳辐射的简化模型

由于房间不在顶层，内墙和天花不受太阳直接照射，且房间上方和南北两侧也为空调房间，因此，笔者忽略了太阳辐射对于内墙和天花的影响.同时，引入室外空气综合温度，将太阳辐射加载在外墙上［5］，计算得到室外空气综合温度.模拟时近似地认为透过窗户的太阳辐射使地板吸热升温，并以热流的形式作用于房间［8］.将玻璃窗吸收的太阳辐射以定温边界条件加载在玻璃窗上.AIRPAK3.0软件利用ASHARE晴天辐射模型计算的东向太阳辐射值和近似的地板平均热流如表3所示.

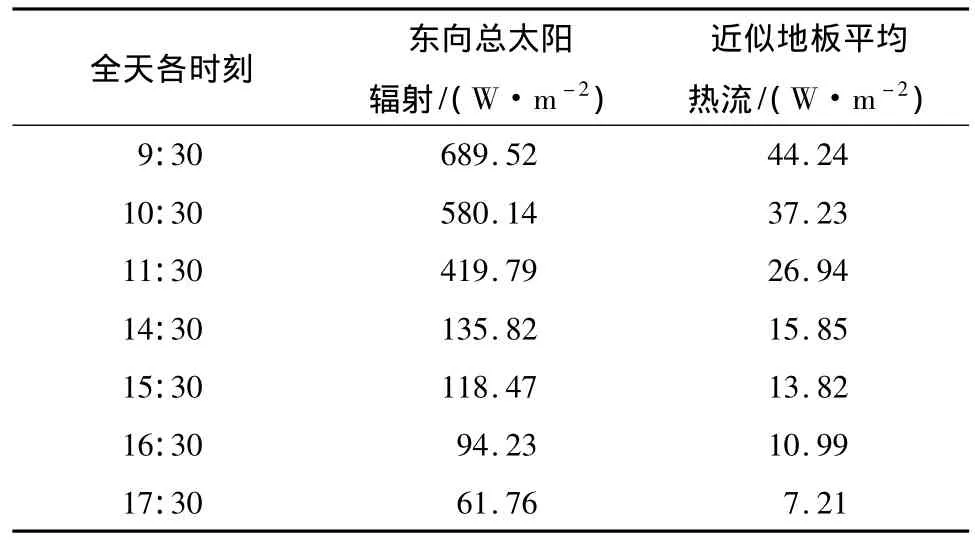
表3 不同时刻东向太阳辐射计算值1)Table 3 Calculated values of solar radiatlon in east direction at specific moments

1.2 数学模型

1.2.1 基本假设

为了使问题得到简化，提出以下假设［9］:(1)室内空气低速流动，可视为不可压缩流体;(2)室内空气为不可压缩粘性流体且满足Boussinesq假设，即由于室内空气流动密度变化不大，密度变化仅对浮升力产生影响;(3)门窗处于关闭状态且气密性良好;(4)忽略人员在室内走动所造成的影响.

1.2.2 数学模型的建立

由于所做的房间模型相对简单，笔者在连续性方程、动量方程和能量方程等控制方程［10］的基础上，引入Chen等［11］提出的改进的Indoor零方程模型以达到微分方程的封闭求解.通过比较发现室内零方程湍流模型计算结果与实验数据吻合得较好［12］，且可以较快获得收敛解.

控制方程通用形式:

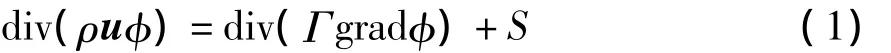
湍流模型:

式中:u为速度矢量;φ为通用变量;Γ为广义扩散系数;S为广义源项;ρ为空气密度，kg/m3;μt为湍流粘性系数;v为风速，m/s;l为湍流脉动长度，m.

1.3 网格划分

采用AIRPAK3.0软件进行建模和网格划分，由于房间结构比较简单，故采用长方体结构化网格，网格加密后共生成331826个节点、52254个独立单元.

2 现场实测

2.1 实验设备

实验中利用A543热线式风速仪测量各计算时刻围护结构外围的空气温度、室内风速、室内温度、室内空气相对湿度.其风速的测量范围为0.05～5.00m/s，精度为0.01 m/s;温度的测量范围为0～60℃，精度为0.1℃;相对湿度的测量范围为2%～98%，精度为0.1%.利用Fluke59红外测温仪测量各计算时刻内墙内表面温度、外窗内表面温度，测量范围为－18～275℃，精度为0.2℃，误差±2%.

2.2 数值模拟的准确性验证

为了验证数值模拟的准确性，在上午8:30，散流器颈部平均风速为3.2m/s，送风温度在16℃，送风相对湿度85.85%时，测量了各职员头部上方0.2m高度处的温度和风速，并与数值模拟结果进行了对比，结果如表4所示.

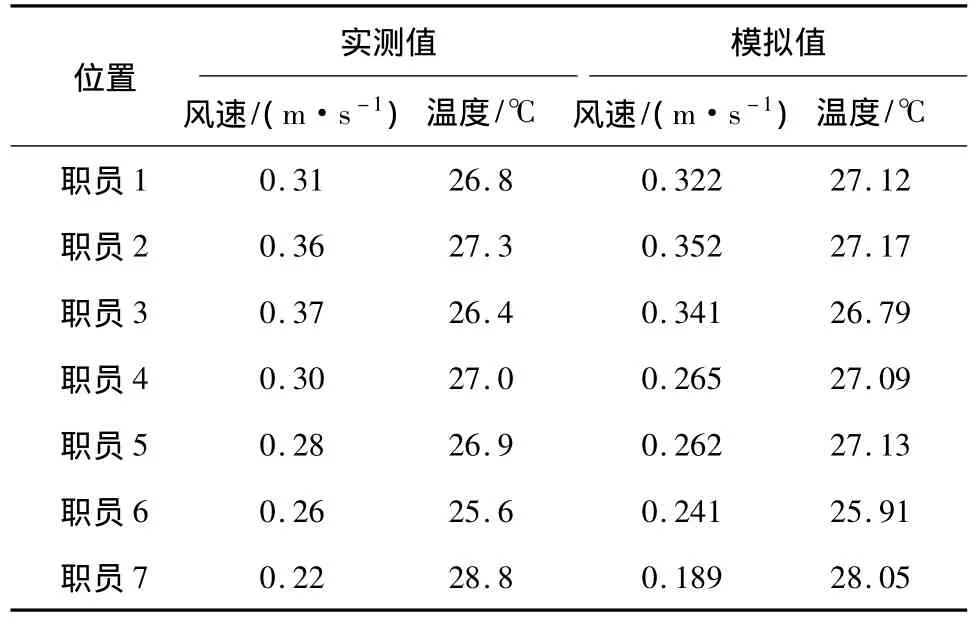
表4 模拟结果与实测值的对比Table 4 Comparison between actual and simulatied values

由表4可见，职员7位置温度的模拟值与实测值偏差稍大，这主要与太阳辐射在模拟时的简化模型有关.总体来看，风速和温度的模拟值相对于实测值的偏差较小，能够反映房间内的实际气流组织情况.

3 数值模拟

由前文对比可知，模拟值在一定程度上能够反映真实值.在此基础上，笔者分别在各计算时刻(9:30、10:30、11:30、14:30、15:30、16:30、17:30)选取送风温度分别为16、17、18、19℃，散流器颈部平均风速分别为2.0，2.5，3.0 m/s，送风含湿量为10.5g/kg进行模拟，得到不同条件下的12组参数，以确定不同送风条件下的室内热舒适性和气流组织情况.各时刻维护结构外侧空气温度、内墙内表面平均温度、玻璃内表面温度的测量值和室外空气综合温度的计算值如图3所示.

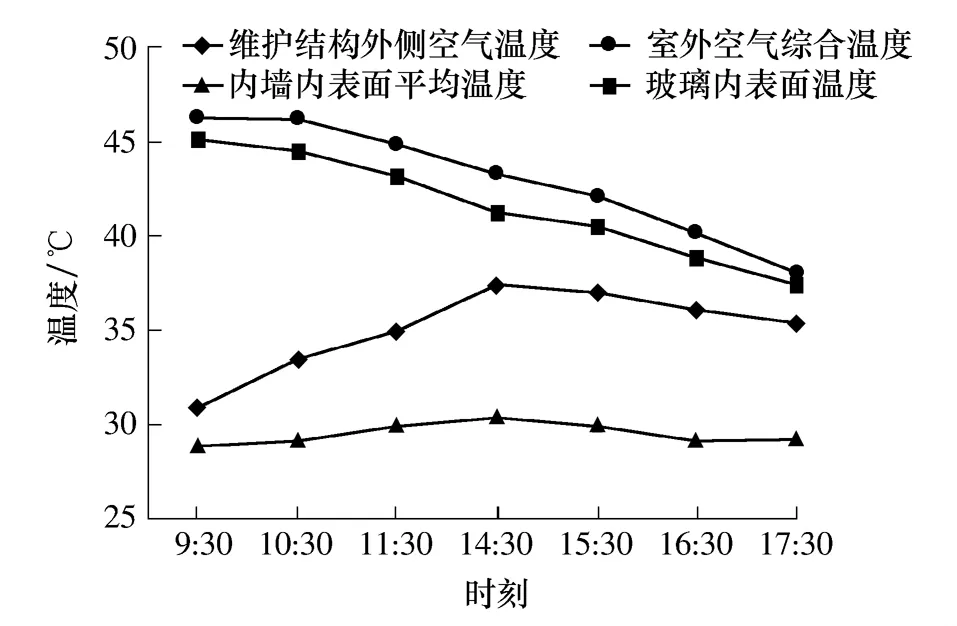
图3 不同时刻温度边界条件的计算值和测量值Fig.3 Calculated and measured valuesoftemperature boundary conditions at different moments

4 结果分析

4.1 送风参数变化对空调房间舒适性的影响

根据Fanger的热舒适性理论［13］，人处于室内时，考虑到人体的新陈代谢以及外界综合因素的影响，可以用热舒适性评价指标PMV来衡量人体的热舒适程度.其综合考虑了人体活动情况、衣着情况、空气温度、空气湿度、空气流速、平均辐射温度6个因素对于人体热舒适性的影响.计算公式如式(3)所示:

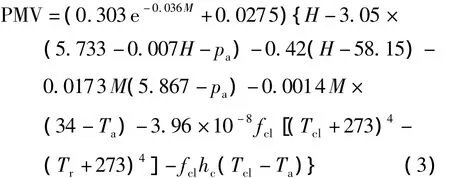
式中:M为人体新陈代谢率，W/m2;H=M－W，W为人体所做的机械功，W/m2;pa为水蒸气分压力，kPa;fcl为穿衣面积系数;Tcl为衣服外表面温度，K;Tr为平均辐射温度，K;Ta为人体周围环境温度，K;hc为对流换热系数，W/(m2·K).

根据 ISO7730:1994中的推荐指标［14］，选择－0.5＜PMV＜0.5作为室内热舒适性的参考区间，并以此作为评价室内热舒适性的依据.其中人员为夏季着装，穿衣面积系数取为0.8;人员为静坐状态，对外做功为0 W/m2;办公室人员新陈代谢率为69.8W/m2;其他参数可通过软件中的热舒适性模块计算得到.

比较发现，两种送风参数相差最大的条件下，工作区域的相对湿度相差1.9%，且当人体静坐时，湿度对于人体的热舒适性影响较小［15-16］，故在分析时，忽略湿度差别对热舒适性产生的影响.

对上午10:30时各送风条件下的室内热舒适性进行模拟计算，得人员工作区域(各隔断内)的PMV平均值如图4所示.

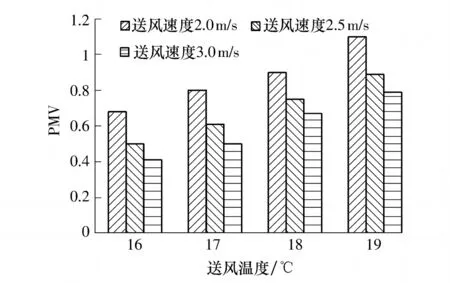
图4 送风参数与PMV的关系Fig.4 Relationship between air supply parameters and PMV

对图4分析可知，送风速度与送风温度对室内热舒适性均有一定的影响，且影响程度不同.当送风含湿量为10.5g/kg，送风温度和送风速度的搭配分别为16℃、2.5 m/s，16℃、3.0 m/s，17℃、3.0 m/s时，室内的热舒适性能够满足ISO7730:1994中的推荐指标－0.5＜PMV＜0.5，且较接近PMV=0.5的临界值.因此，取上述的3种情况进行具体分析，3种送风条件下人体呼吸高度的空气龄图如图5所示.

3种工况下工作区域各参数平均值如表5所示.由表5可知，在上述3种工况下，人体的头脚温差均未超过3℃，满足舒适性要求.人体头部高度的平均风速均满足《采暖通风与空气调节设计规范》中舒适性空调夏季风速小于0.3 m/s的规定.当送风温度为17℃时，冷冻供水温度较高，且3.0m/s的送风速度使空气龄最小.因此可以认为送风温度17℃.散流器颈部平均风速3.0 m/s、送风含湿量10.5g/kg，为满足室内热舒适性的最佳工况.

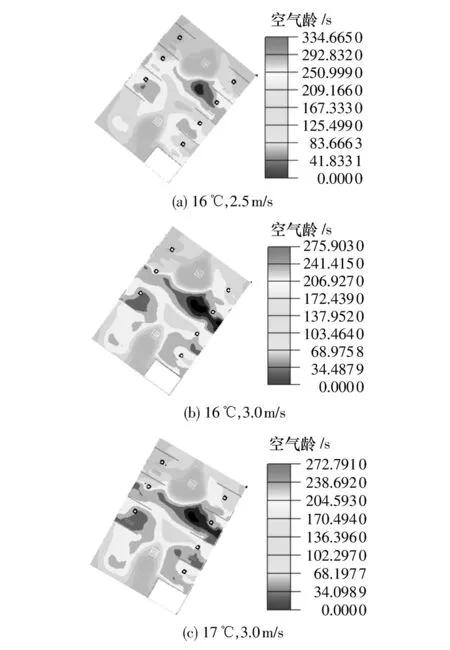
图5 不同送风参数下的空气龄图Fig.5 Mean age of air contours under different air supply parameters

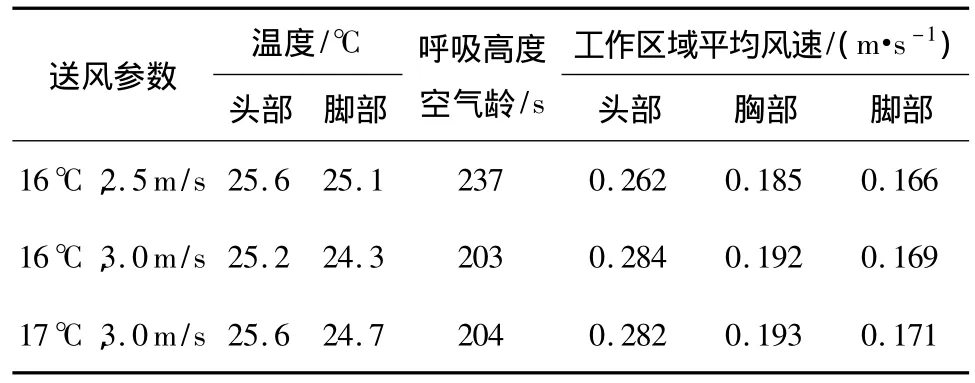
表5 3种不同工况下室内环境参数的模拟结果Table 5 Simulation results of indoor environment parameters under three different conditions

4.2 送风参数优化节能效果分析

4.2.1 各时刻最优送风参数的选取

按照相同的方法，笔者通过数值模拟的方式分别确定该办公类建筑在上班时间各时刻送风温度和送风速度对室内热舒适性的影响，并给出了最适合的送风速度和送风温度.各边界条件按照图3和表3所示，确定的最佳送风参数如表6所示.

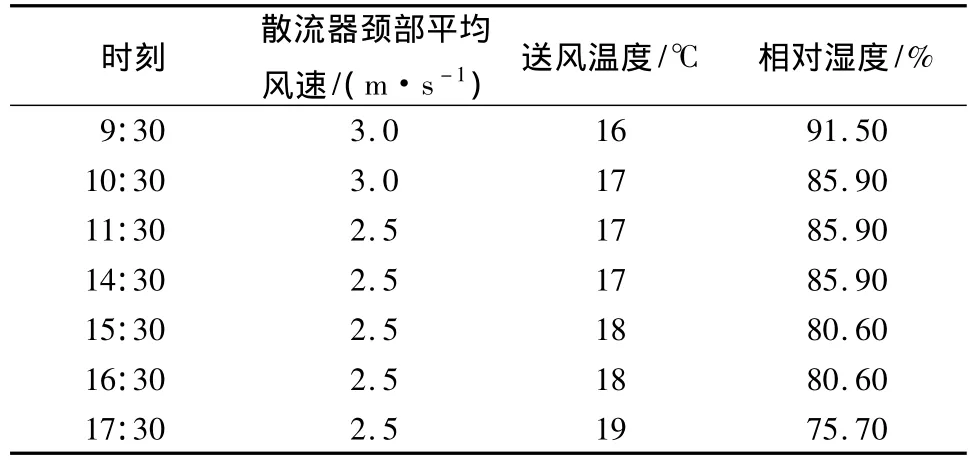
表6 送风参数的优化组合Table 6 Optimum combination of air supply parameters

同时，根据数值模拟结果，当室内实际人数为4～8人时，在表6提供的的最优送风参数下，PMV仍介于－0.5至0.5之间，即室内实际人数与设计人数偏差较小时，计算得到的优化送风参数仍能满足室内的热舒适性要求.

4.2.2 节能效果分析

对于风机盘管而言，其表冷器的制冷量可由下式计算:

式中:Q为风机盘管制冷量，kW;G为空气的质量流量，kg/h;h1、h2为进、出表冷器的空气焓值，kJ/kg.

为了计算风机盘管在全天各时刻的制冷量，并与优化工况下的理论制冷量进行对比，笔者从上午9:30开始每隔一小时测量一次送风口和回风口的空气温度、相对湿度，并根据式(4)计算出风机盘管实际制冷量，结果如表7所示，按优化工况模拟时的风机盘管制冷量如表8所示.

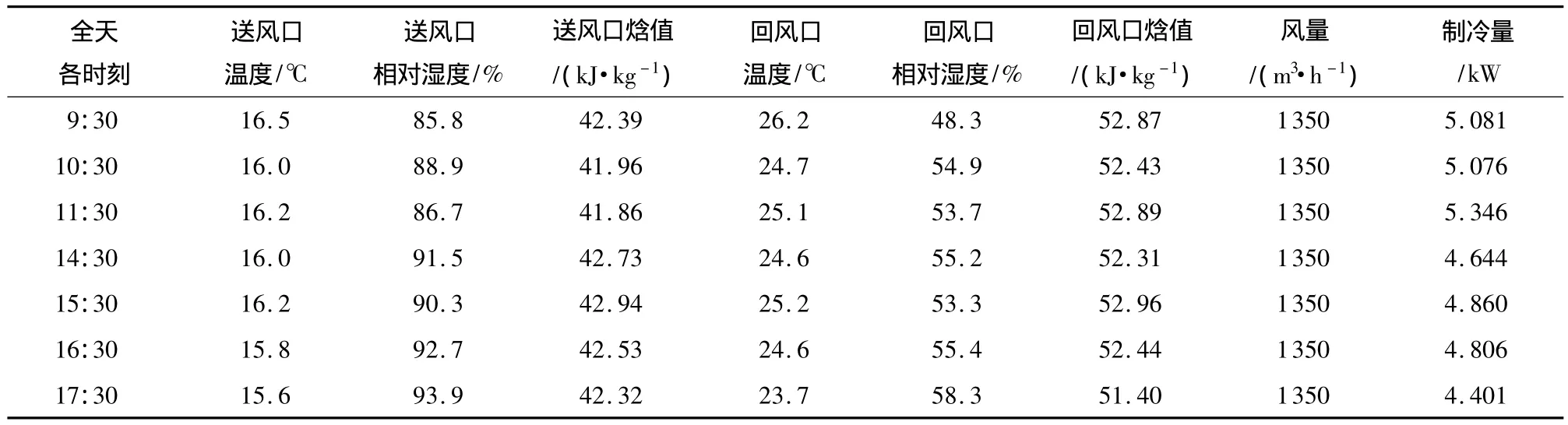
表7 未进行参数优化时的风机盘管制冷量Table 7 Cooling capacity of fan-coil unit based on un-optimized parameters

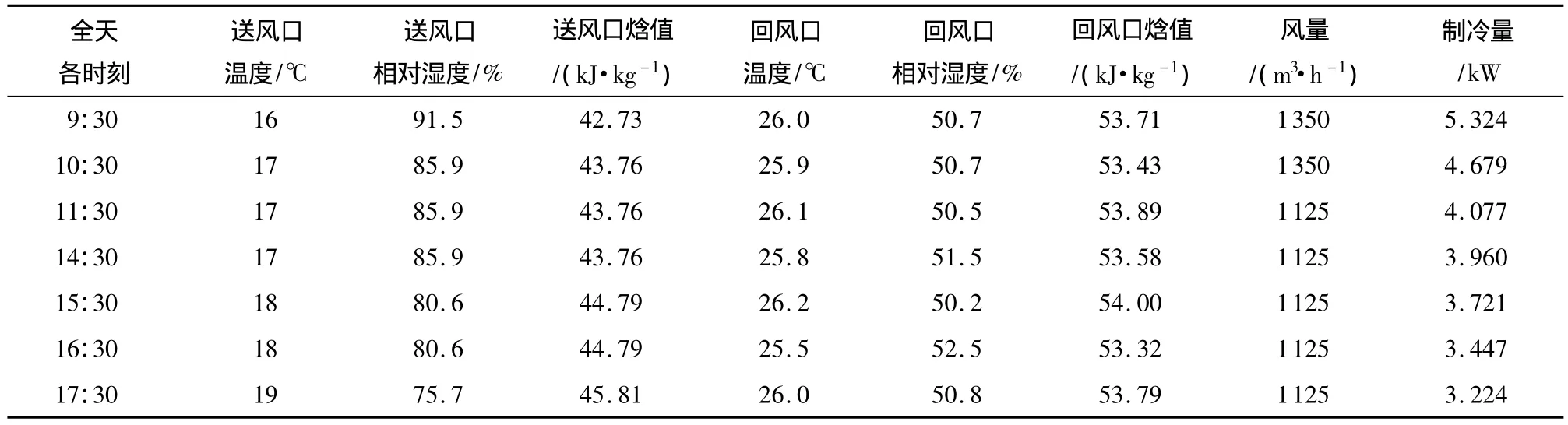
表8 按模拟结果优化参数时的风机盘管制冷量Table 8 Cooling capacity of fan-coil unit based on optimum parameters according to simulation results

分析可知，在不进行优化时，全天部分时刻风机盘管回风温度明显偏低，风机盘管制冷量较高，而根据房间冷负荷的变化规律和模拟结果合理调节送风参数可节省17%的风机盘管制冷量，对于空调末端节能具有一定的参考价值.

5 结语

文中利用AIRPAK3.0数值模拟软件，采用室内零方程湍流模型，对文中建立的办公室物理模型在空调末端供冷条件下的室内气流组织进行了数值模拟;以PMV为指标衡量人体的热舒适程度，研究了空调末端送风温度和送风速度对于热舒适性的影响;对一天内各典型时刻的送风参数进行了优化，得出了各典型时刻在满足热舒适性条件下的送风参数的最优组合.优化后的末端工况与实际末端工况的对比结果显示，空调末端的节能空间较大;优化后的送风参数在全天内有较大波动，根据外界环境合理优化送风参数对空调末端节能有一定的指导意义.

［1］ 李召泼，张小松，吴智深.大型公共建筑中央空调的节能与监控［J］.建筑节能，2010，38(3):62-65.Li Zhao-po，Zhang Xiao-song，Wu Zhi-shen.Energy-saving and control of central HVAC in large public buildings［J］.Building Energy Efficiency，2010，38(3):62-65.

［2］ 陈玉远.中央空调冷源与水系统的研究［D］.重庆:重庆大学城市建设与环境工程学院，2006.

［3］ 陈曦.办公室内空调系统对舒适度及细菌传播的影响［J］.暖通空调，2006，36(11):113-116.Chen Xi.Influence of HVAC system on indoor comfort and bacteria spread in an office building［J］.Heating Ventilating＆Air Conditioning，2006，36(11):113-116.

［4］ 薛若军，王革，方磊.空调房间内热舒适度的数值模拟［J］.哈尔滨工业大学学报，2005，37(8):1145-1147.Xue Ruo-jun，Wang Ge，Fang Lei.Numerical simulation of thermal comfort degree in air-conditioning room［J］.Journal of Harbin Institute of Technology，2005，37(8): 1145-1147.

［5］ 陆耀庆.实用供热空调设计手册［M］.北京:中国建筑工业出版社，2007:216-250.

［6］ 李先庭，赵彬.室内空气流动数值模拟［M］.北京:机械工业出版社，2009:78-79.

［7］ 赵彬，李先庭，彦启森.方形散流器空调室内空气流动的数值模拟［J］.力学与实践，2002，24(5):25-27.Zhao Bin，Li Xian-ting，Yan Qi-sen.Numerical simulation of air distribution inside a room air-conditioned by a square diffuser［J］.Mechanics and Engineering，2002，24 (5):25-27.

［8］ 王磊，龚波，余南阳.自然通风热舒适性［J］.哈尔滨工业大学学报，2009，41(12):254-258.Wang Lei，Gong Bo，Yu Nan-yang.The research of the thermal comfort in natural ventilation buildings［J］.Journal of Harbin Institute of Technology，2009，41(12):254-258.

［9］ 帕斯卡S V.传热与流体的数值计算［M］.张正，译.北京:科学出版社，1984:13-18.

［10］ 王福军.计算流体动力学分析［M］.北京:清华大学出版社，2004:7-12.

［11］ Chen Q，Xu W.A zero equation turbulence model for indoor air flow simulation［J］.Energy and Buildings，1998，28(2):137-144.

［12］ 赵彬，李先庭，彦启森.用零方程湍流模型模拟通风空调室内的空气流动［J］.清华大学学报:自然科学版，2000，41(10):109-113.Zhao Bin，Li Xian-ting，Yan Qi-sen.Simulation of indoor air flow in ventilated room by zeroequation turbulence model［J］.Journal of Tsinghua University:Science and Technology，2000，41(10):109-113.

［13］ Fanger P O.Thermal comfort［M］.New York:Robert Ekrieger Pnblish Company，1982.

［14］ ISO7730:1994，Moderate thermal environments-determination of the PMV and PPD indices and specification of the conditions for thermal comfort［S］.

［15］ Tanabe S，Kimura K.Effects of air temperature，humidity and air movement on thermal comfort under hot and humid conditions［J］.ASHRAE Transactions，1994，100 (2):953-967.

［16］ Marc E Fountain，Edward Arens，Xu Teng-fang.An investigation of thermal comfort at high humidities［J］.ASHRAE Transactions，1999，105(2):94-103.