轴压－弯曲联合荷载下功能梯度材料圆柱壳的屈曲*

黄怀纬 韩强 魏德敏

(华南理工大学土木与交通学院，广东广州510640)

近年来，新型的功能梯度材料(FGM)以其优异的力学、热学性能，在科学研究领域和尖端工程领域受到广泛关注.目前，对于FGM板壳弹性屈曲问题的研究已较为深入［1-6］.Wu等［1］研究了FGM圆柱壳的线性热屈曲行为，得到了结构屈曲载荷的解析解;Li等［3］研究了轴压FGM夹心圆柱壳的线性屈曲问题;Zhao等［6］采用一种无网格 kp法研究了带有圆孔FGM板在热荷载下的屈曲问题;但关于FGM圆柱壳弯曲屈曲性能的研究鲜见报道.

在联合荷载作用的情况，普通圆柱壳的屈曲问题一直以来备受学术界关注［7-9］，但对于FGM圆柱壳的研究却较少涉及.Shen等［10］采用边界层理论结合奇异摄动法研究了轴向与侧向联合荷载下FGM圆柱壳的后屈曲;Shariyat［11］研究了轴向和侧向荷载下FGM圆柱壳的热屈曲性能，分析中考虑了热弹耦合效应，该研究尽管涉及了联合荷载，但研究重点主要在瞬态热屈曲方面.

文中采用Donnell壳体理论和本征值计算方法，将理论研究与数值模拟相结合，研究了轴压－弯曲联合荷载作用下FGM圆柱壳的屈曲问题.

1 理论推导

根据文献［12］，静载下含缺陷FGM圆柱壳的线性屈曲控制方程为

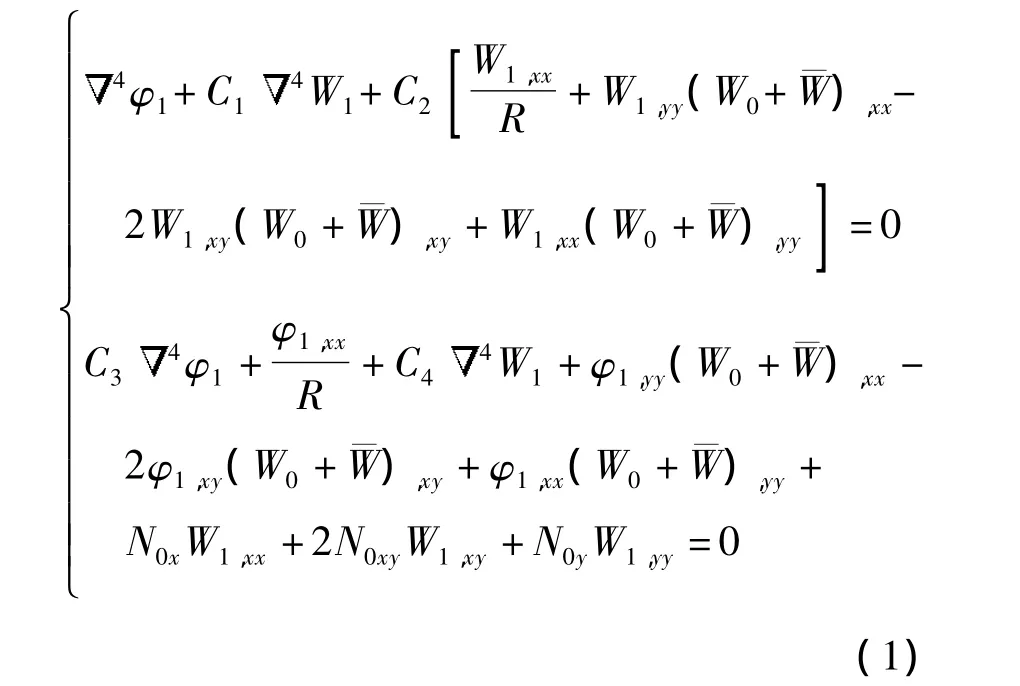
式中:x、y分别表示壳体轴向和周向坐标位置，下标中的逗号表示偏导数，如 W1，xy=∂2W1/∂x∂y;N0x、N0y、N0xy为前屈曲轴向、周向和扭转内力;W0、W1为前屈曲、屈曲挠度;¯W为初始几何缺陷;φ1为应力函数;R为壳体中面半径;C1、C2、C3、C4为与材料和壳体尺寸相关的参数.

忽略前屈曲变形、初始几何缺陷的影响，并将W1和φ1写成W和φ，式(1)可写为

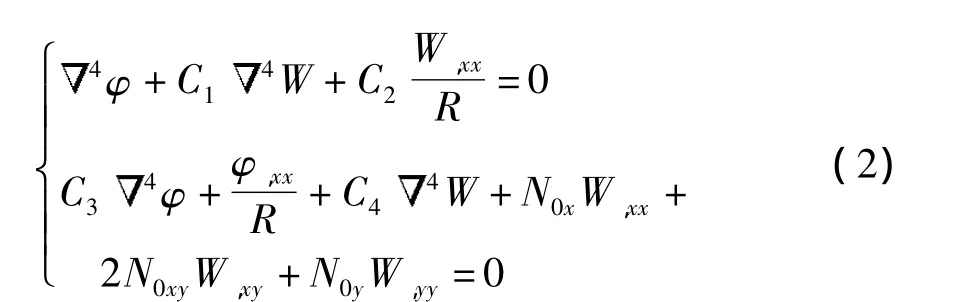
假设FGM圆柱壳在弯矩M和前屈曲轴向内力N0x的共同作用下，其应力分布沿壳体截面方向呈线性变化规律，假设由弯曲引起的截面最大平均应力为σ，如图1所示.

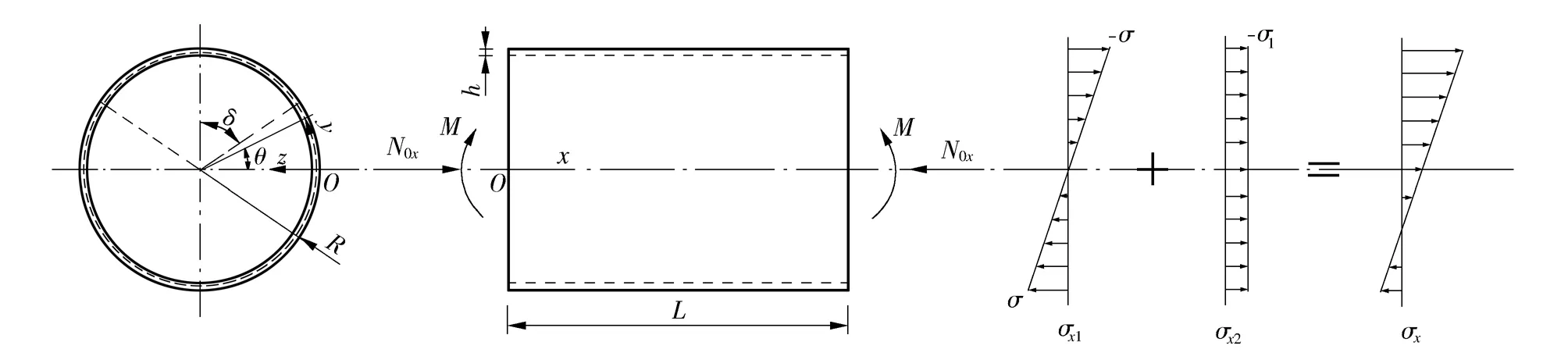
图1 荷载与应力分布示意图Fig.1 Sketch of loading and stress distribution

由于dM=－σx1hR2sinθdθ=σhR2sin2θdθ，则弯矩M可表示为

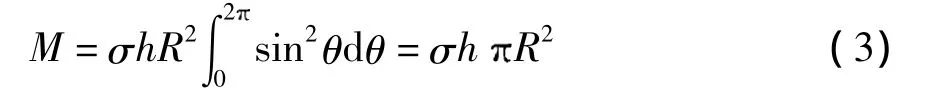
其中，h为壳体厚度;θ为周向转角.

由此，FGM圆柱壳的前屈曲内力可表示为

代入式(2)得到在轴压和弯曲联合荷载作用下的屈曲控制方程:

式中，a=C1C3－C4，b=C2/R2，c=(C1+C2C3)/R.将联合荷载下的屈曲挠度表示为

式中:

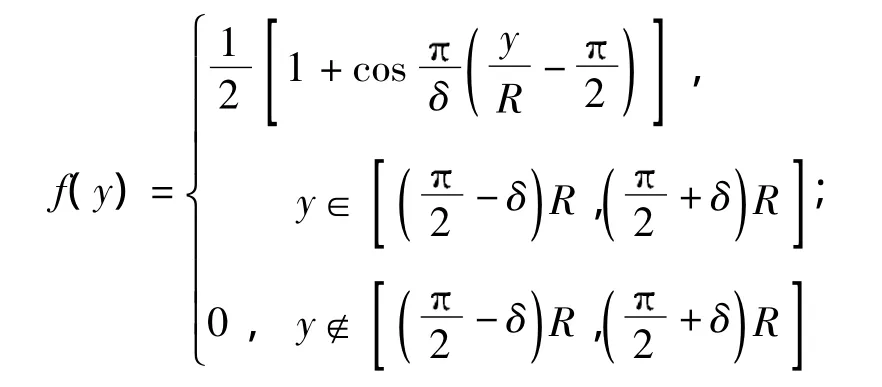
Wb、Wc分别为弯曲和轴压引起的屈曲挠度;η、ζ分别为相应的屈曲挠度幅值;L为壳长;m为轴向半波数，这里假设轴压和弯曲引起的轴向半波数一致;n为屈曲周向波数;δ表示弯曲屈曲波形发生的范围.上述屈曲挠度满足简支边界条件:

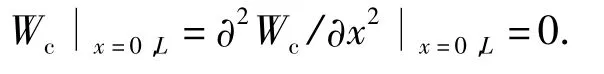
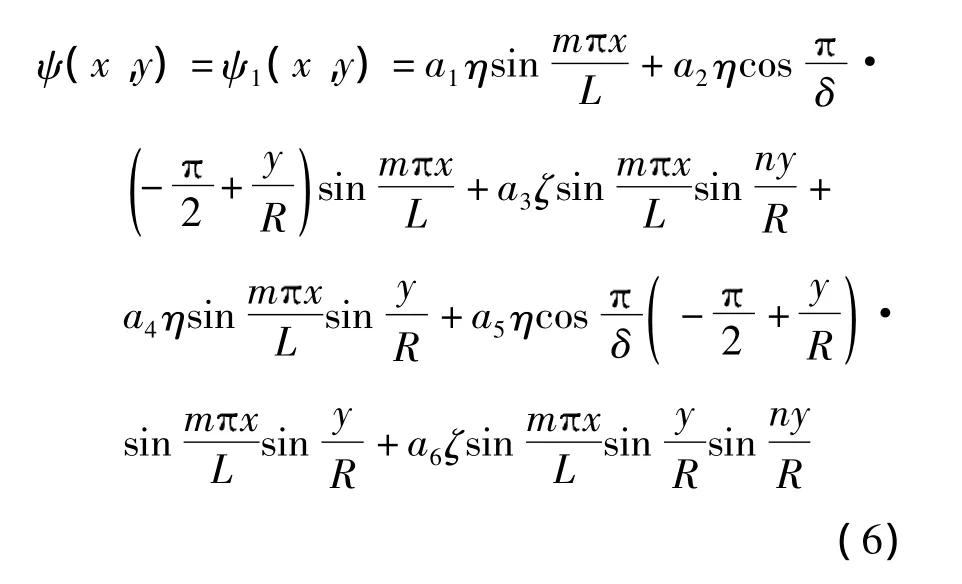
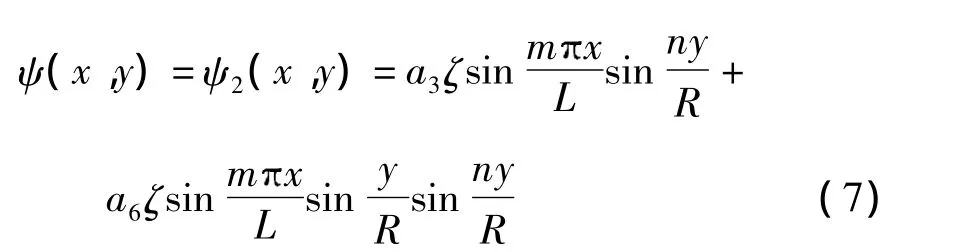
式中，a1，a2，…，a6为相应的系数.

应用Galerkin原理，有

由上式得到:

式中，α11、α12、α21、α22为与材料和结构尺寸相关的系数.为了使得ζ、η存在非零解，得到弯曲－轴压联合荷载下FGM圆柱壳屈曲的临界条件:

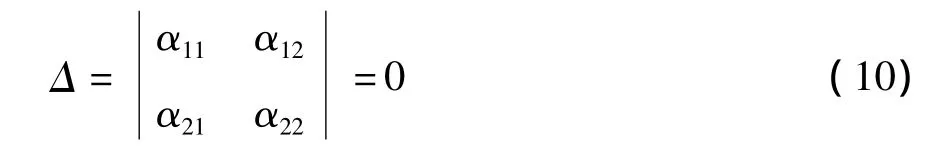
2 结果分析

文中引入采用有限元软件ABAQUS的数值结果对理论分析进行验证，该软件可定义任意壳体截面，从而定义了FGM的物性梯度，结合其本征值屈曲分析模块，可得到结构的屈曲临界状态.

采用ZrO2/Ti-6Al-4V FGM的材料数据［12］，材料属性可表示为

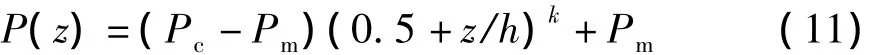
式中:Pc、Pm分别为陶瓷和金属的材料属性，可表示相应的弹性模量、泊松比等材料参数;k为材料组分参数.

取温度为300K时的材料属性;k=1，L=R= 50mm，h=0.5mm，引入参数=δ/、=R/L.

不同轴压预载下FGM圆柱壳的屈曲临界状态的理论预测和ABAQUS数值结果(数值模拟的n值难以计算，故未给出)如表1所示，可见理论与数值的屈曲临界弯矩相吻合，且随着轴压逐渐增大，临界弯矩呈线性下降趋势.通过ABAQUS计算，图2给出了相应的轴压预载下FGM圆柱壳的弯曲屈曲模态.

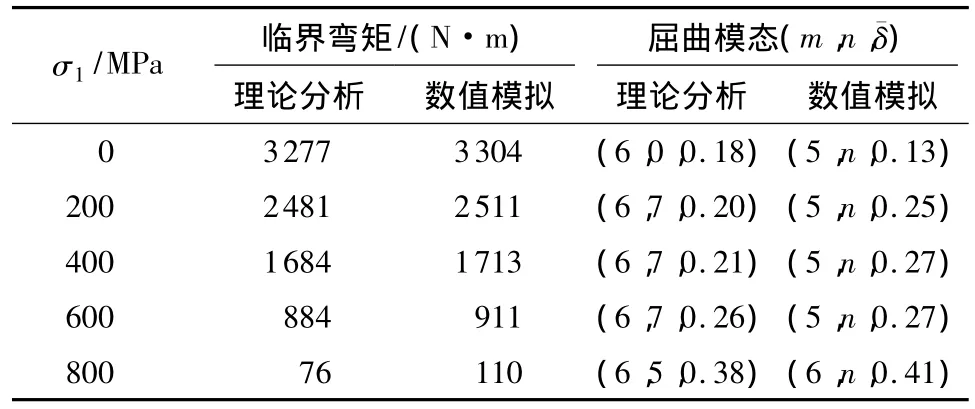
表1 不同轴压预载下FGM圆柱壳的临界弯矩和屈曲模态Table 1 Critical buckling moments and buckling modes of FGM cylindrical shells under various axial compression preloads

图2 不同轴压预载下FGM圆柱壳的弯曲屈曲模态1)Fig.2 Buckling modes of bended FGM cylindrical shells under various axial compression pre-loads 1)自左向右σ1=0，200，400，600，800MPa

FGM圆柱壳尺寸取L=R=50 mm、h=0.5 mm，轴压预载σ1分别为0、200、400 MPa时，组分参数k对壳体屈曲临界弯矩的影响如图3所示.计算结果表明，壳体屈曲临界弯矩随着组分参数的增加而减小，这说明陶瓷含量越多，临界弯矩越大.

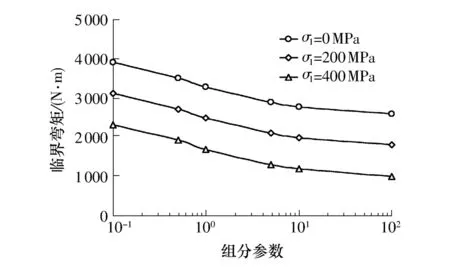
图3 轴载下组分参数对FGM圆柱壳屈曲临界弯矩的影响Fig.3 Effects of inhomogeneous parameter on buckling critical moment of FGM cylindrical shells under axial compression

3 结语

文中研究了弯曲－轴压联合荷载作用下FGM圆柱壳的屈曲问题，假设弯曲荷载和轴压荷载引起的轴向屈曲半波数始终一致，采用本征值屈曲分析方法得到了弯曲和轴压联合荷载作用下壳体的屈曲临界条件.理论分析和数值模拟结果相互印证，证明了理论结果的合理性.模拟结果表明:随着轴压的逐渐增大，屈曲临界弯矩呈线性下降趋势，同时组分参数对壳体屈曲临界弯矩有较大影响，即FGM材料中陶瓷组分的增大将使得屈曲临界弯矩增大.

［1］ Wu L H，Jiang Z Q，Liu J.Thermoelastic stability of functionally graded cylindrical shells［J］.Composite Structures，2005，70(1):60-68.

［2］ Samsam Shariat B A，Eslami M R.Thermal buckling of imperfect functionally graded plates［J］.International Journal of Solids and Structures，2006，43(14/15):4082-4096.

［3］ Li S R，Batrab R C.Buckling of axially compressed thin cylindrical shells with functionally graded middle layer［J］.Thin-Walled Structures，2006，44(10):1039-1047.

［4］ Zhang J H，Li S R.Dynamic buckling of FGM truncated conical shells subjected to non-uniform normal impact load［J］.Composite Structures，2010，92(12):2979-2983.

［5］ 黄怀纬，韩强.侧压下含缺陷功能梯度材料圆柱壳的屈曲［J］.华南理工大学学报:自然科学版，2008，36 (6):40-46.Huang Huai-wei，Han Qiang.Buckling of imperfect functionally graded cylindrical shells under lateral pressure［J］.Journal of South China University of Technology: Natural Science Edition，2008，36(6):40-46.

［6］ Zhao X，Lee Y Y，Liew K M.Mechanical and thermal buckling analysis of functionally graded plates［J］.Composite Structures，2009，90(2):161-171.

［7］ Ellinas C P，Croll J G A.Elastic-plastic buckling design of cylindrical shells subject to combined axial compression and pressure loading［J］.International Journal of Solids and Structures，1986，22(9):1007-1017.

［8］ Vaziri A，Estekanchi H E.Buckling of cracked cylindrical thin shells under combined internal pressure and axial compression［J］.Thin-Walled Structures，2006，44(2): 141-151.

［9］ Shen H S，Xiang Y.Buckling and postbuckling of anisotropic laminated cylindrical shells under combined axial compression and torsion［J］.Composite Structures，2008，84(4):375-386.

［10］ Shen H S，Noda N.Postbuckling of FGM cylindrical shells under combined axial and radial mechanical loads in thermal environments［J］.International Journal of Solids and Structures，2005，42(16/17):4641-4662.

［11］ Shariyat M.Dynamic thermal buckling of suddenly heated temperature-dependent FGM cylindrical shells under combined axial compression and external pressure［J］.International Journal of Solids and Structures，2008，45 (9):2598-2612.

［12］ Huang H W，Han Q.Buckling of imperfect functionally graded cylindrical shells under axial compression［J］.European Journal of Mechanics A/Solids，2008，27(6): 1026-1036.