辅助信息在数据缺失时的应用

罗 薇，曾琼军

(1.暨南大学 经济学院，广州 510632；2.广东工业大学 管理学院，广州 510520)

1 问题的提出

数据缺失是几乎所有的抽样调查都无法避免的问题，一般来说，数据缺失主要由以下几方面的原因造成：抽样框没能覆盖目标总体中的全部单元；样本单元没有参与调查；样本单元没有回答某些调查项目；或者出现一些明显不合逻辑、有意造假的数据。数据缺失不但减少了接受调查者的实际单位数，而且可能扩大估计量方差，严重时还会带来估计量偏差，甚至造成抽样的无效。在数据收集过程中，有许多方法可以用来处理缺失数据。这些方法的共同目的都是要将缺失的数据寻找回来。例如对无回答样本进行重新调查，但是由于成本或其他种种原因的限制无法进行重新调查，或者重新调查也不能获得回答。此时，我们就要关注数据处理阶段对无回答的补救，如采用辅助抽样框将缺失数据与抽样总体单元进行某种方式的联接，或者利用有关辅助资料对缺失数据进行推算，计算缺失数据带来估计量偏差的影响程度。上述问题的解决都有赖于辅助信息运用。本文仅讨论项目无回答背景下的处理，但其方法对单位无回答情况有参考意义。

设目标总体为U，包含N个抽样单元，Y为目标变量，X为与目标变量Y存在较高相关性的辅助变量，则有：

Xi为第i个调查单元的已知辅助信息，q为辅助变量的个数，εi为残差，其均值为零，与Xi相互独立。

上式可以化为：

2 辅助信息在加权调整法中的应用

保证回答集中辅助变量的加权总值等于实际辅助变量的总体总值：

（2）利用辅助信息，调整样本的初始权数di，使得di=ωi，即在等式（4）约束下，使得di与ωi的距离最小，下面采用较为简单的线性校准估计，距离函数表达为：

利用拉格朗日定理求解线性距离最小化得：

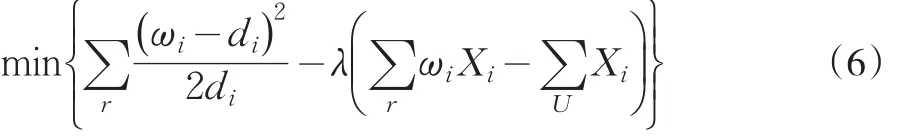
解得：

即：

从而校准估计量为：

即：

校准估计的方差估计量为：

其中：

上述情形为总体辅助信息已知。如果只有样本辅助信息，在项目无回答发生时，校准估计可以利用样本辅助信息调整无回答集的分布，使得回答单位集辅助信息的分布与样本辅助信息的分布较为一致，从而减少无回答误差，此时，校准估计的条件约束方程组为：

则校准估计量为：

3 利用辅助信息进行插补

插补的基本原理是用已有的数据替代调查中的缺失数据，然后利用调查所收集的数据或模拟出缺失数据对总体参数进行估计。已有的数据可以通过两种方法获得：一是以前进行过类似的调查，或存在与缺失数据相关的辅助信息，如果变量之间存在函数关系，建立起反映数据之间相互关系的模型，则可以对缺失数据进行推算估计。但是变量之间往往不存在函数关系，这就限制了这一方法在实际中的应用。二是利用当前正在进行的调查数据，即利用样本中回答数据模拟缺失数据的样本单位，如均值插补、随机插补、热卡和冷卡插补、距离函数配对法、回归估计插补，而这类方法可能会人为地扭曲数据的真实分布。而在相关的辅助信息下，模拟的精度往往得以提高。

sr是对目标变量y回答单元的集合，sm是对目标变量y数据缺失单元的集合，为补上缺失数据yi而造出的插补值，下面将讨论不同插补方法。

（1）均值插补法

（2）随机插补法

为了避免均值插补中插补值形成一个人造“峰值”的缺陷，我们按照某种概率抽样的方法从回答单位数据中随机抽取插补单位，以抽取的插补单位的实际回答值代替缺失值。即在样本回答集中，在r个回答单元中随机抽取m个回答单元，替代m个缺失数据，若j∈sr使得p(=yj) =1 r，则=yj。这一方法弥补了均值插补中插补值过分集中的缺点，但是增加了一个再抽样的过程，必然导致方差的增加。如果能利用相关辅助信息对样本单位进行事后分层，再在每层中进行随机插补，则调整效果较好。

（3）热卡和冷卡插补法

热卡插补就是先根据辅助变量的信息将样本分为若干层，使得层内各单位特征尽可能相似，然后按照某种概率抽样的方法，从当前正在进行调查的同层回答单位中抽取与无回答单位数量相同的样本，以抽取的样本单位数据作为缺失数据的插补值。由于热卡插补抽取的数据与缺失数据具有相似性，所以插补出的数据比较准确，且插补后仍可以保持数据的回答分布形式。如果缺失数据由当前调查外的其他信息，如历史数据进行插补，则称为冷卡插补。

（4）距离函数配对法

采用离缺失数据最近的回答数据作为插补值，若j∈sr使mindist(xi,xj)则=yj。距离函数一般是辅助变量的函数，所选择的辅助变量在性质上应与目标变量相似，且两者应具有密切关系。

（5）回归插补法

回归插补法需要完整的辅助变量x1,…xq和目标变量估计目标变量y对线性关系建立回归方程，则：

此时的插补值是通过标准方法（如最小平方法）计算出来的预测值，它所产生的插补值比均值法得到的插补值更为稳定。往往可以采用前期数据作为辅助变量来预测现期数据。而当辅助信息x1,…xq相同时，得到的插补值也一样，同样会产生样本扭曲的问题。

4 利用辅助信息构造间接估计量

由于缺失数据的分布一般来说是随机的，所以采用插补法推算缺失数据，样本方差将增大，估计量也是有偏的，同时，上述各插补方法也要求完整的辅助信息。下面研究在一般情况下，即在一些目标变量数据和一些辅助信息都缺失的情况下，利用回答数据和已知辅助信息构造间接估计量来处理无回答。

设目标总体U的样本为s，第i个单位的包含概率为πi[1]，将样本分成三个不相交的子集：s1表示目标变量和对应辅助信息都完整的集合，s2表示目标变量无回答但辅助信息存在的集合，s3表示目标变量存在但辅助变量不存的目标变量的集合，其对应的样本量分别为n1，n2，n3，且1≤n2,n3≤n/2[2]。要估计总体均值，一方面可以先对各子样本考虑估计量，然后进行加权平均或相加，求得总体均值的估计量。令总体均值为：

如果β未知，利用广义最小二乘法，固定样本下β的最小线性无偏估计量即为样本回归系数，则为的线性无偏估计量。而未抽中单元均值估计量为=，所以：

另外，根据样本的结构，也可以利用所有已知目标变量和辅助变量来推断缺失数据，估计总体参数。子样本s1，s2，s3的Horvitz-Thompson估计量为：

则目标变量Y和辅助信息X的总体总量估计分别为：

相应的比估计量和回归估计量为：

其中，X是辅助变量的总体总量，如果b未知，取b=cov(x,y)/var(x)。M.M.Rueda，S.Gonza′lez和A.Arcos的数据模拟研究证明，与简单回归估计插补相比，上述间接估计量的精度可以大大地提高[4]。

5 结论

综合上述各种方法不难发现，利用辅助信息，加权校准估计能调整样本回答集的发布，使其更好地代表总体的分布，提高估计量的精度。采用辅助信息模拟缺失数据的插值法，简单易明，能够减少估计量的偏差。但传统的插值法也存在这样或那样的缺点，如扭曲样本的分布，低估方差，稳定性较差，需要完整的辅助信息。而利用间接估计量进行插补，方法虽较为复杂，但是在一部分目标变量和一部分辅助信息缺失的情况下，利用所有已知的目标变量和辅助信息，能够提高估计量的精度。

[1]刘建平等.辅助信息在抽样调查中的应用模型与方法[M].北京:中国统计出版社，2008.

[2]Valliant,A.H,Dorfman，R.M.Royall.Finite Population Sampling and Inference[M].London：John Wiley,2000.

[3]H.Toutenburg，V.K.Srivastava.Efficient Estimation of Population Mean Using Incomplete Survey Data on Study and Auxiliary Characteristics，Sonderforschungsbereich[C].Discussion Paper179,2000.

[4]M.M.Rueda，S.González,A.Arcos.Indirect Methods of Imputation of Missing Data Based on Available Units[J].Applied Mathematics and Computation，2009,(175).

[5]金勇进.非抽样误差分析[M].北京:中国统计出版社，1996.