对Jahangir组合式矩估计器的改进
2012-03-15李大朋
李大朋 姚 迪
(北京理工大学电子信息工程学院,北京 100081)
对Jahangir组合式矩估计器的改进
李大朋 姚 迪
(北京理工大学电子信息工程学院,北京 100081)
在M.Jahangir以常数为权的组合式矩估计器的基础上,给出一种以函数为权的组合式矩估计器,称为L-J估计器.其中,最优加权函数是根据U估计器与形状参数的单调关系,通过数论网格最优化算法搜索解出.大量仿真实验证实,在对K分布形状参数v大范围的参数估计中,L-J估计器在估计精度上,不但较Jahangir等提出的常数加权组合矩估计器的精度有显著提高,而且可与MLE(Maximum Likelihood Estimator)相当.特别是由于MLE作为渐进无偏估计量,需要充分大的样本长度才能达到最优,这就使得L-J估计器的估计精度可在样本长度较小时优于MLE.此外,L-J估计器无需迭代运算,因而在计算效率上,显著优于现有的ML估计器.
K分布;U估计器;组合式矩估计器;ML估计器
K分布杂波模型是目前应用较为成功的雷达遥感图像统计模型之一,它能很好地描述高分辨雷达图像的统计分布特性,在海杂波、地杂波描述以及其他领域都有着广泛的应用.其参数估计一直是研究的热点问题.研究表明[1],对K分布形状参数v的错误估计会引起CFAR(Constant False Alarm Rate)检测性能严重下降.因此对K分布形状参数v的正确估计,具有重要意义.
虽然理论上,最大似然估计(MLE,Maximum Likelihood Estimator)是K分布形状参数v的最佳渐进无偏估计,其渐进分布是以真值为均值,方差为Crammer-Rao下界的正态分布.但是,迄今很难得到ML估计的闭型解,而通过数值方法,需要大量的迭代运算,计算量巨大[2-3].为此,很多学者提出了不同的参数估计方法来替代ML估计.
文献[4]提出了一种由U估计器与幅度对比算子估计器以常数为权组合而成的新型估计器.其性能较单一的矩估计器的性能有显著提高,向MLE靠近了一步.
文献[5]提出了另外一种以常数为权的由U,X估计器组合形成的新型的K分布形状参数估计器,称为M估计器.M估计器在小v值,即v在0~2的范围内优于U,X等其他所有非组合型矩估计器,在0<v<2的范围内其性能与Jahangir提出的估计器类似.文献[6]提出了对M估计器的改进,扩大了M估计器的应用范围.不过,改进的M估计器仍然属于以常数为权的组合式K分布形状参数估计器,其估计精度仍与Jahangir估计器相差不多.
本文给出以函数为权的组合式矩估计器,记为L-J估计器.实验证实,L-J估计器对K分布形状参数v估计的精度与效率,不但显著优于上述以常数为权的组合式K分布形状参数估计器,而且可达到接近或相当于MLE的精度;特别是在样本长度较小、v较大时,L-J估计器的精度甚至在v的某些取值范围内超过MLE的精度.此外,由于L-J估计器不必像ML估计器那样进行大量的迭代运算,其在计算效率方面较MLE有着显而易见的优势.
1 K分布形状参数v的矩估计器
1.1 K 分布
K分布的密度函数(PDF)为
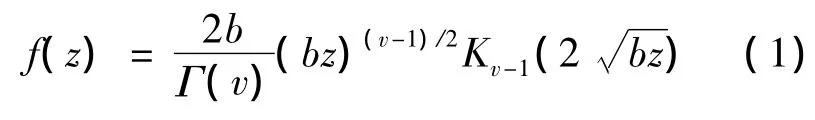
其中,z≥0为信号强度;Kv-1是 v-1阶第二类修正Bessel函数;v>0为形状参数;b=v/μ为尺度参数;μ为杂波均值.
1.2 U 估计器[2]

其中,ψ(0)是双 gamma函数;γ是 Euler常数,γ=0.57721.
1.3 J 估计器[4]

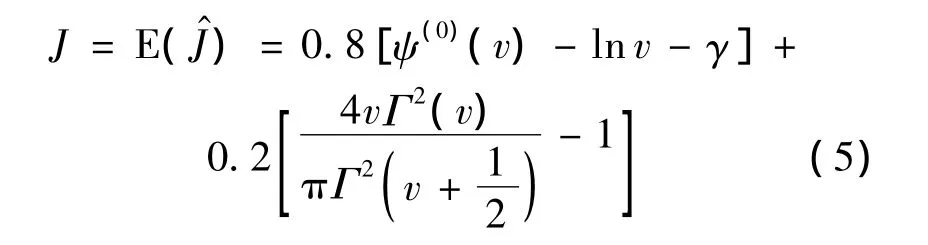
2 L-J估计器
正如文献[4]指出的,以常数为权进行两个矩估计的这种组合,所得估计器的性能只能是次优而达不到最优.因此,为使组合式矩估计器达到最优而与MLE相当,提出以函数为权的组合式矩估计器,记为L-J估计器.
L-J估计器:
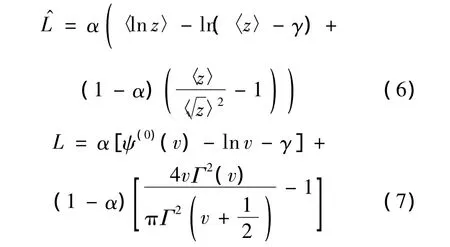
由于式(3)的函数是U关于v的单调递增函数,即可推知U估计器的期望U与K分布形状参数v互为反函数,具有单值、单调的一一对应关系.也就是说,U的变化可以完全反映v的变化.这就成为选取U做控制权函数α=α(U)变化的自变量的理论根据.
为确定α=α(U)的具体表达式,需建立两个n(n∈Z+,n≥3)元数组 x和 y.由于在 n的取值范围内求α=α(U)的基本原理是一样的,故以下为便于说明和理解,仅以n=3的情况为例.
设有两个三元数组:
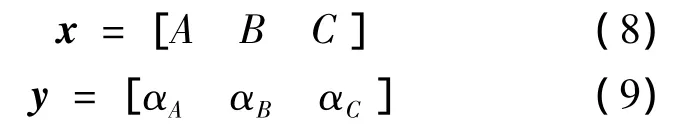
利用matlab数学软件中的pchip函数对x,y进行分段三次Hermite插值[7],即可得到插值函数:

其中,A,B,C为U定义区间内待定的3个点,αA,αB,αC为 α的与 A,B,C三点对应的待定的3个值.
为确定 A,B,C 和 αA,αB,αC的具体数值而得到函数 α(U)=pchip(x,y,U),先给出 Fuzzy 数学中Hamming距离的概念:对m∈N,为比较点集(s1,s2,…,sm)与点集(t1,t2,…,tm)“距离”的远近,Fuzzy数学定义这两个点集的Hamming距离:

由Fuzzy数学可知,d越小,两个点集靠得越近.于是,寻求L-J估计器的最优估计的最优化问题就是通过Monte-Carlo实验,寻求适当的A,B,C和 αA,αB,αC,使得点集(σvL_1,σvL_2,…,σvL_m)与点集(σvMLE_1,σvMLE_2,…,σvMLE_m)之间的 Hamming距离达到最小.其中,(σvL_1,σvL_2,…,σvL_m)及(σvMLE_1,σvMLE_2,…,σvMLE_m)分别为 L-J估计器、ML估计器,在v1,v2,…,vm共m个仿真点上得到的对 v的估计的标准差点集.则,A,B,C 和 αA,αB,αC这6项的具体值,就可以通过求Hamming距离d的最小值的6维最优化搜寻获得.最优化搜索的方法有多种,例如遗传算法、模拟退火法、粒子群算法等等.本文采用数论网格方法.运用数论网格(SNTO)方法进行最优搜索,最后结果如下:

即得分段三次Hermite插值函数:

为实际运用,将此matlab中的pchip函数表示成分段三次Hermite插值函数,得函数表达式:

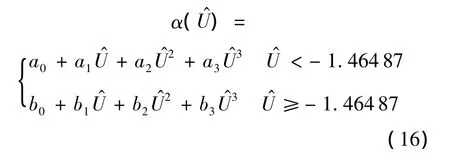
其中
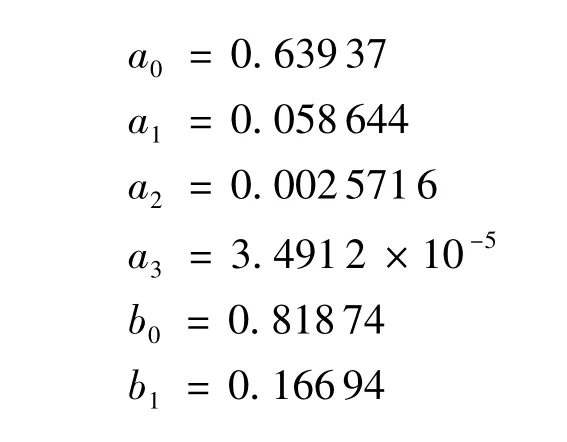
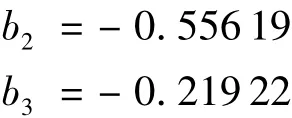
3 仿真实验
文献[2]提出的MLE,限于多种因素影响,即使样本长度N=1000时,所得数据的标准差仍然很大,没有达到理论最优值.文献[2]中MLE与J,L-J估计器标准差的比较详见表1(为便于比较,实验条件保持与文献[2]一致,均为:N=1000,Monte-Carlo实验次数为1000).

表1 M LE,J,L-J估计器标准差情况比较
由表1可以看出,L-J估计器在上述情况下所得估计的标准差最小,估计精度优于该MLE.
文献[8]采用期望最大(EM)迭代算法实现了另一种对K分布参数的ML估计.但正如文献[9]指出的那样,虽然其运算较二维平面搜索有所减小,但有关迭代运算仍需要相当大的数据量才能保证计算的精度,额外的计算量还是比较大.下面给出L-J估计器与文献[8]中MLE及J估计器误差情况的比较.
图1给出在样本长度N=750的情况下,L-J估计器与文献[8]中MLE及Jahangir估计器的估计误差比较.易见,即使样本长度很大,L-J估计器与MLE的估计精度也很接近.
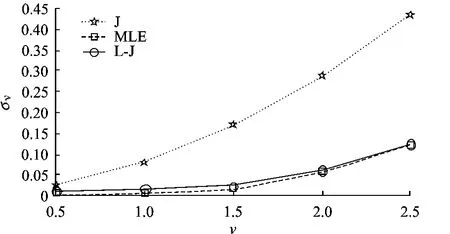
图1 N=750时,MLE,L-J与 J估计器对形状参数v估计的标准差比较
而由图2可以看到,当样本长度N=500时,L-J估计器与文献[8]中MLE的估计精度更加相近,而且随着v值增大其精度已在部分点上超过MLE.
图3给出在样本长度N=250时,L-J估计器与文献[8]中MLE及其他估计器的估计误差比较.不难看出,此时L-J估计器的估计精度总体上优于MLE.

图2 N=500时,MLE,L-J与 J估计器对形状参数v估计的标准差比较
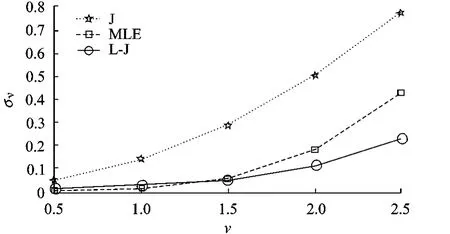
图3 N=250时,MLE,L-J与 J估计器对形状参数v估计的标准差比较
由图1~图3的结果可见,随着样本长度的减小和v值增大,文献[8]中MLE的估计精度越来越不如L-J估计器.其原因在于:
1)MLE是渐进的无偏估计.MLE要达到最优估计,是有条件的,要求样本长度充分大.所以,MLE的估计精度会随样本长度减小而减小.
2)文献[8]给出的EM算法,需要大量的迭代运算,且估计精度与初值关系很大.初值给偏,不但会造成迭代次数增加,同时也会造成估计误差的增大.
为全面比较,图4和图5给出样本长度N=250,经10000次Monte-Carlo仿真实验,在小v值和大v值两种情况下,L-J估计器与Jahangir提出的J估计器的标准差的比较.由图可见,L-J估计器的精度在很宽的v值的范围内,显著优于J估计器.

图4 N=250,v∈[0.1,2]时,L-J与 J估计器对v估计的标准差比较
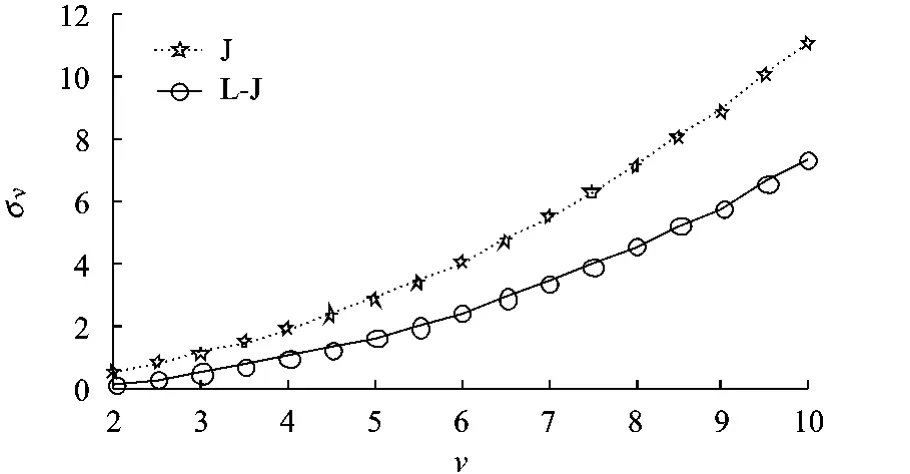
图5 N=250,v∈[2,10]时,L-J与 J估计器对v估计的标准差比较
4 结 束 语
为了对K分布形状参数v尽可能准确的估计,国内外学者进行了大量研究,提出了多种估计器,例如近期成果[10-12].迄今这些估计器大体可分为两类:矩估计器和ML估计器.研究表明,这两类估计器各有短长:矩估计器计算量小但精度低,而ML估计器精度高,是理论上的对N的最优估计,其缺点是:要求样本长度N充分大,并且运算量较大.
文献[4]提出了一种以常数为权的通过两个矩估计器组合而成的新型估计器,性能优于单一的矩估计器.理论与实践都证明,这种以常数为权的组合式矩估计器的性能只能是次优的,不可能达到最优.
本文提出L-J估计器,改变了组合式矩估计器只能以常数为权的现状.L-J估计器是一种由U估计器和对比度算子估计器组合而成,以函数为权的组合式矩估计器.大量仿真实验证实,L-J估计器在估计精度上不但显著优于Jahangir提出的J估计器,而且在样本长度较小时,其精度在v的某些范围内甚至优于现有MLE;而从估计效率上看,L-J估计器无迭代过程,因而其估计效率明显优于MLE.
References)
[1] Armstrong B C,Griffiths H D.CFAR detection of fluctuating targets in spatially correlated K-distributed clutter[J].IEE Proceedings-F,1991,138(2):139 -152
[2] Joughin IR,Percival D B,Winebrenner D P.Maximum likelihood estimation of K-distribution parameters for SAR data[J].IEEE Trans on Geosciences and Remote Sensing,1993,31(5):989-999
[3] Blacknell D.Comparison of parameter estimators for K-distribution[J].IEE Proc-Radar,Sonar,Navigation,1994,141(1):45-52
[4] Jahangir M,Blacknell D,White R G.Accurate approximation to the optimum parameter estimate for K-distributed clutter[J].IEE Proc-F,1996,143(6):383 -390
[5]郝程鹏,侯朝焕,鄢锦.一种新的K分布形状参数估计器[J].电子与信息学报,2005,27(9):1404 -1407 Hao Chengpeng,Hou Chaohuan,Yan Jin.A new estimator for estimating the parameters of K-distribution[J].Journal of Electronics& Information Technology,2005,27(9):1404 - 1407(in Chinese)
[6]郝程鹏,侯朝焕.一种K分布杂波背景下的双参数恒虚警检测器[J].电子与信息学报,2007,29(3):756 -759 Hao Chengpeng ,Hou Chaohuan.A two parameter CFAR detector in K-distribution cluuter[J].Journal of Electronics & Information Technology,2007,29(3):756 -759(in Chinese)
[7]张德丰.MATLAB数值计算方法[M].北京:机械工业出版社,2010:143-147 Zhang Defeng.Numerical computing with MATLAB[M].Beijing:Machinery Industry Press,2010:143 -147(in Chinese)
[8] William J JRoberts,Sadaoki Furui.Maximum likehood estimation of K-distribution via the expectation-maximization algorithm[J].IEEE Transaction on Signal Processing,2000,48(12):3303-3306
[9]胡文琳,王永良,王首勇.基于zlog(z)期望的K分布参数估计[J].电子与信息学报,2008,30(1):203 -205 Hu Wenlin,Wang Yongliang,Wang Shouyong.Estimation of the parameters of K-distribution based on zlog(z)expectation[J].Journal of Electronics & Information Technology,2008,30(1):203-205(in Chinese)
[10] Abraham D A,Lyons A P.Reliable methods for estimating the K-distribution shape parameter[J].Oceanic Engineering,IEEE Journal of,2010,35(2):288 - 302
[11]娄昊,张乐锋.雷达海杂波的K分布复合特性[J].火力与指挥控制,2010,35(7):62 -65 Lou Hao,Zhang Lefeng.K-distribution compound characteristics research on radar sea clutter[J].Fire Contral and Command Contral,2010,35(7):62 -65(in Chinese)
[12]张晓利,关键,何友.K分布杂波中分布式目标的Rao检测[J].电子与信息学报,2010,32(10):2496 -2410 Zhang Xiaoli,Guan Jian,He You.Rao test of distributed targets in K-distributed clutter[J].Journal of Electronics & Information Technology,2010,32(10):2496 -2410(in Chinese)
(编 辑:娄 嘉)
Improvement of Jahangir’s multiple moments estimator
Li Dapeng Yao Di
(School of Information and Electronics,Beijing Institute of Technology,Beijing 10081,China)
Based on M.Jahangir's multiple moments estimator using constant weight,a new estimator named L-Jestimatorwas proposed,which consists of multiple moments and uses function weight.The optimum weight function was obtained by the sequential algorithm for optimization according to the monotonic relationship of U-estimator and the shape parameter.A large number of simulation experiments show that the accuracy of L-Jestimator is not only higher than that of Jahangir'smultiple estimator using constant weight noticeably,but also it can stand comparison with that of maximum likelihood estimator(MLE).As an asymptotic unbiased estimation,MLE requires sufficient large number of samples to achieve the optimum performance,then it makes that the accuracy of L-Jestimator can be better than that of MLE in the case of fewer samples.Moreover,the efficiency of L-Jestimator is obviously higher than that of MLE,since there is no iteration to need.
K-distribution;U-estimator;multiplemoments estimator;maximum likelihood estimator
TN 911.23
A
1001-5965(2012)06-0788-05
2011-03-11;网络出版时间:2012-06-15 15:43
www.cnki.net/kcms/detail/11.2625.V.20120615.1543.020.htm l
李大朋(1979 -),男,黑龙江齐齐哈尔人,博士生,ddyao@bit.edu.cn.
