Von Karman模型三维大气紊流仿真理论与方法

高 静 洪冠新 梁灶清

(北京航空航天大学 航空科学与工程学院，北京 100191)

Von Karman模型三维大气紊流仿真理论与方法

高 静 洪冠新 梁灶清

(北京航空航天大学 航空科学与工程学院，北京 100191)

基于三维紊流场相关函数矩阵，用蒙特卡罗法仿真生成Von Karman模型三维空间大气紊流场，实现了对复杂的Von Karman模型的精确推导和应用，仿真流场的相关特性在理论上可以任意逼近Von Karman理论模型.通过提高白噪声序列的白化程度及优化蒙特卡罗算法的方法提高了仿真精度和效率.数值仿真结果证明:所生成的空间大气紊流场符合模型特性，具有较好的统计特性和仿真精度，满足实时飞行仿真对紊流场数据的要求.

大气紊流;蒙特卡罗法;Von Karman模型;数值仿真;飞行仿真

大气紊流对在大气层中飞行的各种飞行器，包括飞机、导弹、运载火箭、空天飞机以及微小型飞行器、气球、飞艇等的设计、使用安全等都有较大影响.大气紊流模型中，与 Dryden模型相比，Von Karman模型的频谱函数在高频段的斜率不同，频谱函数更为复杂，更符合大气紊流的实际情况［1］.在研究涉及飞机结构振动的飞行品质、飞机的结构疲劳等问题时，由于飞机结构模态频率通常恰好处在高频范围，因而高频范围内紊流可能激发飞机的结构振动，只要可行，最好使用Von Karman大气紊流模型.

对大气紊流进行建模与仿真研究中，一维大气紊流序列的仿真一般采用成型滤波器法，此方法要求模型的频谱函数能够进行共轭分解，因此无法基于Von Karman模型进行时域仿真，工程应用较少.但在分析空中加油、编队飞行等多机飞行仿真及飞行品质等研究中，必须使用模型的二维或三维紊流场，且最好采用基于Von Karman模型.文献［2－3］中生成二维紊流场的方法，在理论上有缺陷，各向同性不满足.文献［4］对 Von Karman模型进行有理化逼近，简化了 Von Karman模型，生成的并不是真正的空间三维大气紊流场.文献［5］中提出的空间三维大气紊流场的理论模型和数值方法，摆脱了以上仿真模型的局限，该方法不用对模型进行简化，生成的三维大气紊流场具有良好的均匀性和各向同性.但是文献［5］只是基于 Dryden模型，没有实现基于 Von Karman模型的三维紊流场仿真，且由于需要大样本空间的计算以提高精度，此方法受计算机条件限制，仿真精度和效率都难以令人满意，无法满足工程计算需要.

本文应用蒙特卡罗法基于相关函数矩阵，仿真生成了Von Karman模型三维空间大气紊流场，验证了该方法的正确性，且在算法上进一步完善，仿真生成了精度较高的可应用飞行动力学仿真的三维大气紊流场.

1 Von Karman模型

Von Karman模型的能量频谱函数为

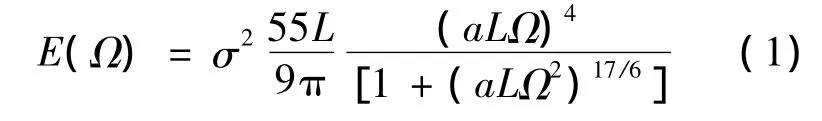
其中，a=1.33;L为紊流尺度;Ω为空间频率;σ为紊流强度.

由此可推得大气紊流Von Karman模型的纵向和横向相关函数如下:

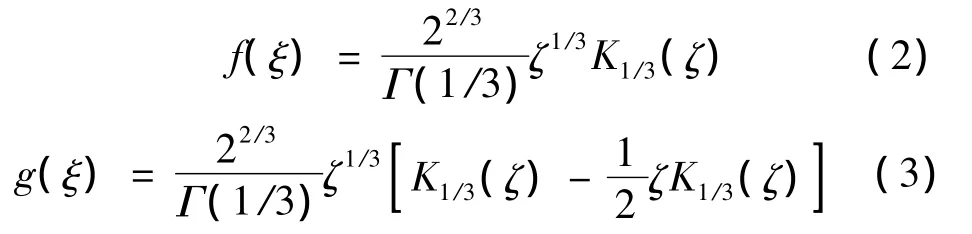
其中，ζ=ξ/(aL);Γ为 Gamma函数;K为 Bessel函数.由于Von Karman模型函数形式复杂，使得常规仿真方法受限.

根据Bachelor公式，得出基于Von Karman频谱的空间相关函数如下:

基于式(4)可构造三维空间大气紊流场的空间相关函数矩阵.

2 三维大气紊流场建模理论

2.1 产生三维高斯白噪声场并将其离散化

用数学库函数产生(0，1)上高斯分布白噪声序列{W}，随机变量为{W1，W2，…，Wmnl}.

白噪声的相关函数等于δ函数:

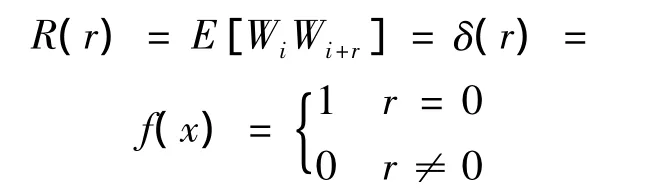
将随机变量Wi按逐行排列方式排布在划分为 m ×n×r的空间网格上，m，n，r分别为沿 X，Y，Z轴方向的网格点数.由此生成了如图1所示的高斯分布三维白噪声场{Z(x，y，z)}.其中 x=1，2，…，m，y=1，2，…，n，z=1，2，…，r，且 Z(i，j，k)=Wp，其中p=(k－1)×m ×n+(j－1)×m+i.

2.2 离散化三维空间随机场的相关函数矩阵

构造一般相关系数矩阵MU={Cij}={R(ij)}，按照图1所示，空间划分为p=m×n×r个网格，则点点相关构造相关系数矩阵的一般表达式为

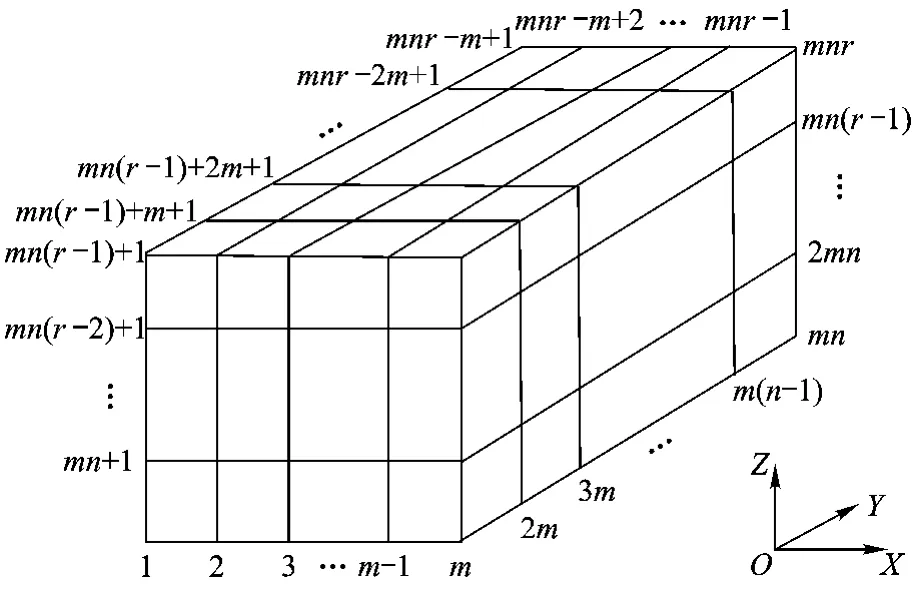
图1 随机变量空间分布示意图

矩阵中Cij为由式(4)得到的基于Von Karman模型的空间相关函数.

2.3 产生满足相关函数矩阵的紊流场

由于MU为对称正定阵，采用Cholesky分解法，可将其分解为一个上三角阵和一个下三角阵的乘积，即MU=AAT.其中，A为下三角阵.设U是需要产生的随机场，取U=AZ，其中，Z=［Z1，Z2，…，Zn］T为白噪声随机变量.

可以证明U是满足相关系数矩阵要求的随机场.

以上三维大气紊流场建模方法，理论完备，可以精确生成任意需要的三维大气紊流场.在实际数值仿真计算中，仿真精度取决于输入的白噪声精度以及紊流的样本空间大小.可以证明，白噪声的白化程度越高，紊流场的样本空间越大，仿真精度就越高，表现在仿真结果上就是仿真曲线和理论曲线贴合得越好.

3 仿真算法

本文采用蒙特卡罗法对三维大气紊流场进行数值仿真.蒙特卡罗法可以对复杂的随机性问题进行求解，方法及程序结构简单，大量简单重复抽样，做出的解答能否反映实际，与原来所建立的数学模型是否正确及输入信息的质量有关，而与本方法无关.由于选用的样本容量有限，因此总会存在误差，提高解的精度则需要成百倍的增长样本的容量.随着计算机的迅速发展，将蒙特卡罗随机模拟的方法应用于研究三维大气紊流场数值仿真中，使得对空间三维大气紊流速度场的高精度仿真得以实现.

3.1 改进的双随机交换法提高输入白噪声精度

由于仿真计算中采用数学库函数生成的伪随机数存在固有缺陷，导致对紊流场的仿真精度存在很大影响［6］.为了提高伪随机数的白化程度，本文采用改进的双随机交换法.主要步骤如下:

1)随机抽取序列x(i－1)(n)的两点数据并互换其位置，得到序列xi(n)，重复执行N次;

2)计算xi(n)的自相关函数 ri和平方和SSi;

3)若SSi＜ε或i达到预定执行运算的最大循环次数Nmax，则停止运行;

4)若 SSi＜ SSi－1，则返回步骤 1)，继续执行运算，反之，放弃在步骤1)中进行的第i次随机双换，并返回步骤1)继续执行.

5)重复执行步骤1)～步骤4)j次，其中Nj=N/10j，若 Nj＜1，则令 Nj=1.

该方法只是对随机数序列进行重新组合，因此不改变随机数样本的方差、均值以及概率密度特性.由于步骤2)、步骤3)的计算量很大，上述方法用较小的计算量获得了较大的白化效果.例如处理一个6 000点序列耗时仅几分钟，随机序列白化程度明显提高.

3.2 相关函数矩阵的计算

Von Karman模型的三维空间大气紊流场计算，是对计算机速度和内存要求较高的海量数据计算.在具有足够大样本容量的计算条件下，计算结果的统计特性将更接近理论值，数据结果的精度也就更高.在计算相关函数矩阵，并Cholesky分解为下三角矩阵的环节，将占用大量计算机内存并耗费大量时间.需采用通过降低程序计算量和优化内存使用的优化算法来提高计算效率，使得在相同的计算条件下可以计算尽可能大的样本空间.

以10×10×10的空间随机场为例，构造的基于Von Karman频谱的纵向相关系数矩阵MU为

其中

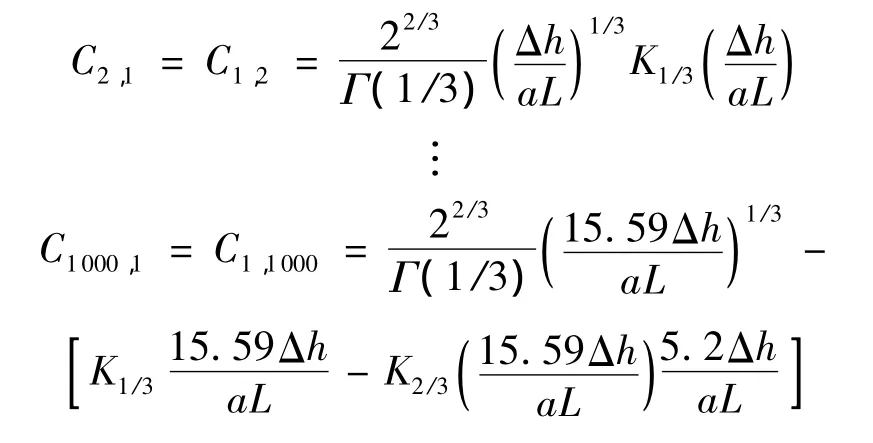
C1，1000表示网格空间中第1点与第1000个点间的相关函数，其余类推;Δh是网格间距步长，为简化表达式，直接按照式(4)计算出了系数;L是大气紊流纵向尺度.

以上Von Karman模型相关函数表达形式虽然复杂，但是由于本建模方法无需对模型表达式进行简化，因此可以进行数值计算.

3.3 仿真大气紊流场的特性检验

三维大气紊流场仿真计算结果是否合理，精度是否满足要求，需要对仿真结果进行相关特性检验.检验的准则就是看仿真紊流序列的相关特性是否符合该紊流模型的相关函数理论表达式［7］.Von Karman模型的纵向和横向相关函数的理论表达式见式(2)和式(3).仿真序列的相关函数如下式:

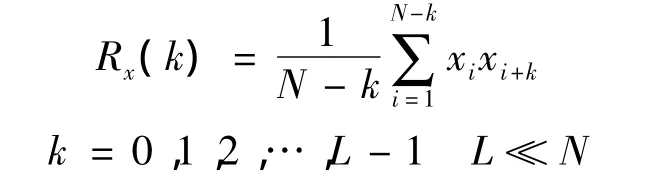
将仿真的相关函数曲线和理论相关函数曲线画在同一幅图上，来衡量它们的贴合程度.

3.4 抽样-检验方法

蒙特卡罗方法提高解的精度需要成百倍地增加样本的容量，而增加样本容量受内存容量和CPU计算速度的限制，这是蒙特卡罗方法通过增加采样点数提高精度的主要限制因素.另一方面，结果的误差难以估计，更是蒙特卡罗法固有的特点.注意到蒙特卡罗法是一个纯粹的抽样方法，本文提出了“抽样-检验方法”:抽样方法采用蒙特卡罗法，检验则是对抽样结果的误差进行统计计算，进而筛选误差达到要求的仿真紊流场.本文对检验长度分段逐段检验来实现，对每段分别设定误差，以实现精细的误差控制，从而得到满足相应要求的仿真结果.按照抽样-检验方法的要求改进后的算法，可以在短时间内完成同一尺度的成千上万个紊流场计算，按照数理统计理论的大数定律，可以从中挑选到相关特性与Von Karman模型吻合度很高的紊流场，这样就不需要成百倍地增加样本的容量而得到更高精度的仿真结果.图2为仿真算法流程示意图.

图2 仿真算法流程示意

4 仿真算例和分析

选取两个算例，用本文方法计算基于Von Karman模型的三维紊流场.这两个算例的紊流场尺度，在常见的紊流场的大尺度范围内，具有典型的工程应用意义.选取紊流强度σ=1m/s，纵向紊流尺度为L=530m.根据反复计算调试，设定比较合理的误差率控制条件，以达到精度和计算效率的双赢.

算例1 网格点数:6000(1500×2×2).检验长度:100点，分3段(40点，30点，30点)逐段检验.U序列的控制误差率为:第1段，0.05;第2段，0.05;第3 段，0.1.V，W 序列的控制误差率为:第1段，0.1;第 2段，2;第 3段，1.计算时间:48min.相关性检验结果见图3.

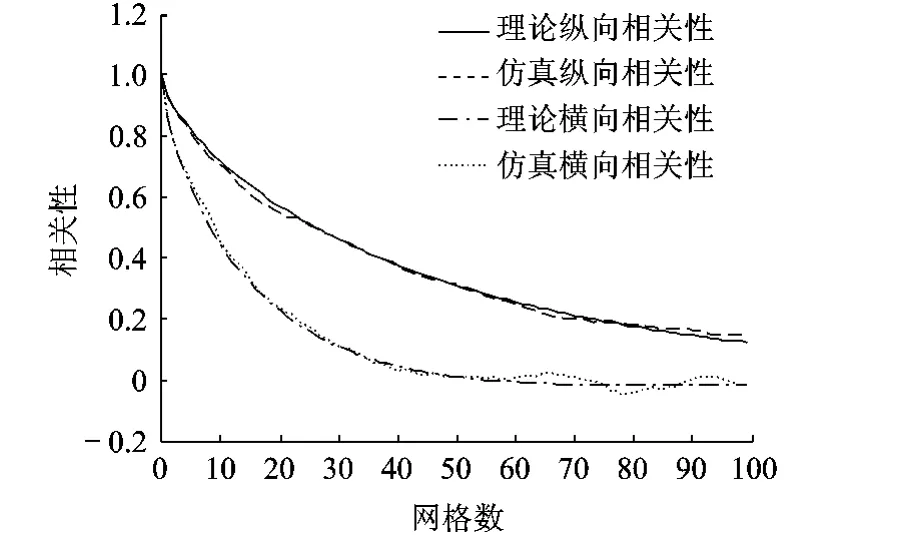
图3 三维大气紊流场(1500×2×2)的相关性检验

算例2 网格点数:8000(2×2000×2).检验长度:100点，分3段(40点，30点，30点)逐段检验.U序列的控制误差率为:第1段，0.05;第2段，0.05;第3 段，0.1.V，W 序列的控制误差率为:第1 段，0.1;第 2 段，1.5;第 3 段，0.75.计算时间:0.25min.相关性检验结果见图4.

图4 三维大气紊流场(2×2000×2)的相关性检验

图5是算例1的Von Karman模型紊流速度序列仿真结果，图6是仿真紊流场(30×30)剖面示意图.

图5 Von Karman模型紊流速度序列仿真结果

本方法未对模型进行任何简化，因此仿真生成的三维空间大气紊流场完全符合所选用的Von Karman大气紊流模型.由图3～图6的相关性检验图、仿真紊流速度图及紊流场剖面图等表明，仿真相关性曲线与理论曲线吻合程度高，与以往其他研究结果相比，仿真精度有了大幅度提高，非常令人满意.另外本文通过具体算法的改进，在计算条件、耗时和结果逼真度之间找到了一个比较理想的平衡方法，计算时间大大缩短，使仿真效率得到提高.

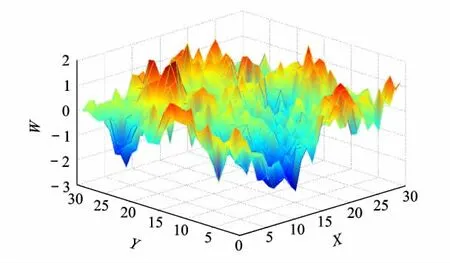
图6 仿真三维空间大气紊流场剖面示意图

5 结论

通过大量计算分析表明，应用蒙特卡罗法基于相关函数矩阵，仿真生成Von Karman模型三维空间大气紊流场的模型方法正确，仿真结果合理，计算精度和效率高.

本文的仿真理论，实现了对复杂的Von Karman模型的精确推导和应用，使得仿真结果在理论上可以无限逼近理论值.在仿真方法上，改进的双随机交换法提高了白噪声的精度，优化了蒙特卡罗方法，采用抽样-检验方法，实现了精细的误差控制，从而解决了蒙特卡罗方法提高解的精度需要海量样本容量和误差控制的困难.本文提出的仿真方法，大大提高了仿真精度和效率.

本方法可直接应用于飞行仿真，使飞行仿真中的风场模拟更加真实，对模拟器的研制具有实际意义，完全符合工程应用需要.在实时飞行仿真中，可对白噪声和确定紊流空间的相关函数矩阵进行预计算，以满足实时仿真需要.如计算条件有限，又需要较大紊流场，可采用基于对称原理的紊流场扩展方法，将生成的局部空间紊流场通过拼接的办法有效扩展为大范围连续紊流场.

References)

［1］ Etkin B.Turbulent wind and its effect on flight［J］.Journal of Aircraft，1981，18(5):327 －345

［2］肖业伦.用于飞行仿真的二维紊流场的数字生成法［J］.航空学报，1990，11(4):124 －129 Xiao Yelun.Digital generation of two-dimensional field of turbulence for flight simulation［J］.Acta Aeronautica et Astronautica Sinica，1990，11(4):124 －129(in Chinese)

［3］陆宇平，胡亚海.基于空间相关函数的二维紊流场数值生成法［J］.南京航空航天大学学报，1999，31(2):139－145 Lu Yuping，Hu Yahai.Digital generation of two-dimensional field of turbulence based on spatial correlation function［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，1999，31(2):139－145(in Chinese)

［4］张峰，汪沛，王冲，等.基于Von Karman模型的三维大气紊流仿真［J］.计算机仿真，2007，24(1):35 －38 Zhang Feng，Wang Pei，Wang Chong，et al.Simulation of threedimensional atmospheric turbulence based on Von Karmanmodel［J］.Computer Simulation，2007，24(1):35 － 38(in Chinese)

［5］洪冠新，肖业伦.蒙特卡罗法仿真生成三维空间大气紊流场［J］.航空学报，2001，22(6):542 －545 Hong Guanxin，Xiao Yelun.Monte Carlo simulation for3-D-field of atmospheric turbulence［J］.Acta Aeronautica et Astronautica Sinica，2001，22(6):542 －545(in Chinese)

［6］马树峰，岳晓奎.大气紊流的数字仿真［J］.计算机辅助工程，2008，17(3):54 －56 Ma Shufeng，Yue Xiaokui.Digital simulation on atmospheric turbulence［J］.Computer Aided Engineering，2008，17(3):54 －56(in Chinese)

［7］肖业伦.大气扰动中的飞行原理［M］.北京:国防工业出版社，1993:166－173 Xiao Yelun.Flight theory in atmosphere turbulence［M］.Beijing:National Defense Industry Press，1993:166 － 173(in Chinese)

(编 辑:李 晶)

Theory and method of numerical simulation for 3D atmospheric turbulence field based on Von Karman model

Gao Jing Hong Guanxin Liang Zaoqing
(School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China)

atmospheric turbulence;Monte Carlo method;Von Karman model;numerical simulation;flight simulation

V 321.2

A

1001-5965(2012)06-0736-05

2011-03-28;网络出版时间:2012-04-01 11:59

http://www.cnki.net/kcms/detail/11.2625.V.20120401.1159.003.html

凡舟青年科研基金资助项目(20080502)

高 静(1981－)，女，陕西子洲人，助理研究员，gaojing@buaa.edu.cn.

Three-dimension-field atmospheric turbulence based on Von Karman model was generated with Monte Carlo simulation，in view of correlation function matrix.According to the derivation of the Von Karman model for mulae，the correlation curves of the simulated field can highly approach the theory results.The precision and efficiency of atmospheric turbulence simulation were improved by using double stochastic interchange minimization algorithm to improve Gauss white noise sequence，and also by the optimization of Monte Carlo method.The simulated atmospheric turbulence field，is identical with the Von Karman model by numerical test，and has perfect statistical characteristic and simulation precision.The simulation method could be used in real-time flight simulation.