载波相位/捷联惯导组合对高轨飞行器的导航

温永智 吴 杰

(国防科技大学航天与材料工程学院，长沙 410073)

载波相位/捷联惯导组合对高轨飞行器的导航

温永智 吴 杰

(国防科技大学航天与材料工程学院，长沙 410073)

高轨飞行器可用卫星数目较少，信号空间链路损耗大，使用伪距进行测量的精度较低.提出基于GNSS(Global Navigation Satellite System)卫星载波相位与捷联惯导紧组合方法对高轨机动飞行器进行自主导航.该方法将连续跟踪的卫星初次可用时的整周模糊度的浮点解作为状态变量，通过平方根UKF建立了组合导航非线性滤波模型，提出了基于整周浮点解交集的滤波器故障检测方法.研究表明，提出的组合导航方法充分利用了载波相位高测量精度和系统性误差缓变的特点，提高了系统的可靠性和精度.

载波相位;捷联惯导;组合导航;故障检测与隔离

目前卫星导航技术的发展对空间资源的利用和人们的生活方式的改善起着越来越重要的作用，并将在未来几十年内进一步发展成熟.可用的卫星导航系统有:美国的 GPS、俄罗斯的 GLONASS、欧洲的GALILEO以及我国的北斗系统.此外，印度、日本也在研制自己的导航系统.充分利用各种卫星资源，是解决飞行器导航高精度、长航时及可靠性等问题的途径之一.

对低轨飞行器(轨道高度在2 000 km以下)的自主导航方法已较成熟.对中轨(轨道高度在2000～20 000 km)和高轨飞行器(轨道高度在20000 km以上)自主导航方法的研究相对较少.对高轨飞行器的自主导航国外已做了相关的论证与试验［1－4］.其中，试验结果表明在近 60 000 km的高度，GPS卫星信号依然能够被捕获，说明用GPS对高轨飞行器导航是可行的.国内学者分析了GNSS对地球同步轨道卫星或登月轨道飞行器进行定轨时的可见性并研究了相应的定轨算法［5－9］.本文研究的基础上对载波相位信息的使用方法作进一步研究.

为了利用载波相位获得高精度的定位结果，并避免整周模糊度求解问题.可采用载波相位时间差分和载波相位平滑伪距等方法.载波相位时间差分将测量噪声的均方差放大了2倍.载波相位平滑伪距，需要一段平滑时间才能稳定，精度受伪距测量精度影响，并且载波测量不能独立进行导航，降低了系统的可靠性.

为了充分利用载波相位的高测量精度和独立性，本文提出将连续跟踪的卫星初次可用时的整周模糊度浮点解作为状态，并用平方根UKF进行信息融合的导航方法.

1 组合导航信息融合模型

1.1 组合导航系统工作模式

采用载波相位观测量和捷联惯导测量信息进行融合.当飞行器自由飞行时，处于失重状态，为了避免加速度计测量误差的影响，认为加速度计的测量数据严格为0.数据融合时滤波器的维数根据飞行器上的轨控发动机是否开机自动进行调整.

当飞行器进行轨道机动时，状态变量由飞行器的位置、速度、姿态四元数、陀螺偏差、加速度计偏差、卫星接收机的钟差、钟差变率及可用卫星对应的整周模糊度向量在当前时刻的浮点解组成，即

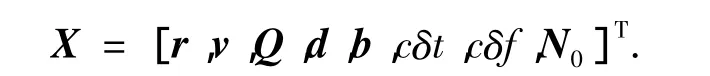
当飞行器自由飞行时，状态变量由飞行器的位置、速度、姿态四元数、陀螺偏差、卫星接收机的钟差、钟差变率及可用卫星对应的整周模糊度向量在当前时刻的浮点解组成，即

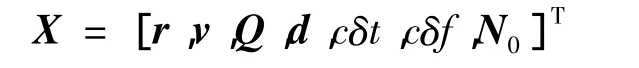
本文可用卫星对应的整周模糊度向量N0是指该卫星初次可用时从卫星到接收机的距离对应的整周模糊度，在该卫星连续跟踪过程中N0在不考虑各种误差影响的情况下应保持不变.

1.2 飞行器状态方程

导航坐标系采用J2000坐标系，文中简称为i系.飞行器的状态方程可表示为式(1).其中地球引力的摄动项考虑到J2项.

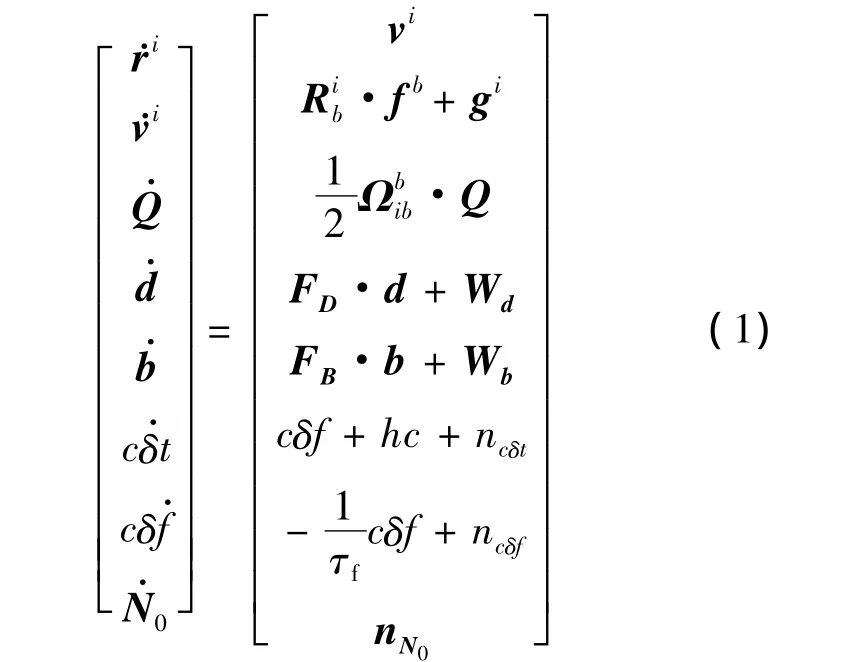
式中，ri，vi为飞行器在i系内的位置、速度向量;Q为飞行器体系(b系)相对于i系的旋转四元数为b系到i系的坐标变换矩阵;fb为视加速度在b系中的值，为加速度计的直接观测量;gi是飞行器所在位置的地球引力加速度向量在i系中的值，由ri计算;为反对称矩阵，由陀螺测得的角速度计算;Wd，Wb分别为相应的过程噪声向量;c为光速;δt为接收机钟差;δf为接收机时钟漂移;τf为接收机钟频漂移的反相关时间;ncδt和ncδf为热噪声;h为考虑相对论效应影响后的时钟频率改正数.

陀螺和加速度计偏差分解为零阶项和一阶随机马尔科夫项，即

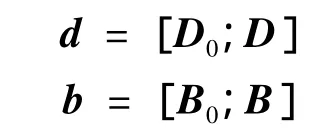
记τD和τB分别为陀螺和加速度计的随机误差的反相关时间，nB和nD为对应驱动白噪声向量.状态微分方程式中，FB和FD的表达式如下:

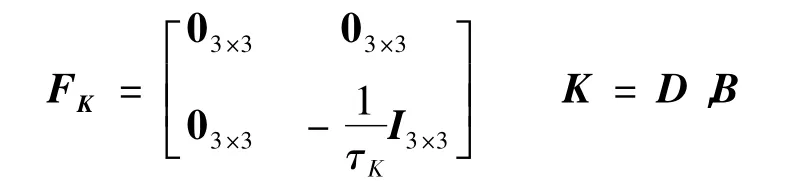
nN0为初始整周模糊度浮点解递推过程噪声，当信号不穿过大气层时，它的大小由卫星钟差校正后残差的变化率和卫星星历误差的变化率决定.当信号穿过大气层时，它的大小除了受卫星钟差变率和星历误差变化率影响外，还受大气延迟误差变化率的影响.

1.3 载波相位观测方程及误差分析

载波相位观测方程可表示为

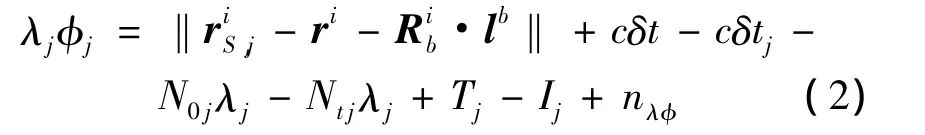
式中，λj为卫星j的载波波长;φj为测量的载波相位卫星在J2000坐标系中的位置;ri为捷联惯导在J2000系中计算的位置;lb为GNSS天线对应的杆臂矢量;cδt为接收机钟差与信号传播速度的乘积;cδtj为卫星钟差与信号传播速度的乘积;N0j为j号卫星在初次可用时刻至飞行器的距离中包含的整周数;Ntj为j号卫星从初次可用时刻到当前时刻，飞行器飞行距离中所包含的整周数，由接收机连续跟踪载波累计的整周数获得;Tj为大气对流层导致的时延误差;Ij为大气电离层导致的时延误差;nλφ为接收机产生的随机噪声.

高轨飞行器与GNSS卫星之间的相对位置如图1所示，飞行器只有在图中阴影部分显示的区域才能收到可用的GNSS卫星信号.对于穿过大气层的信号，由于信号不但有延迟误差还有折射造成的误差，为了避免这种误差的影响只使用不穿过大气层(信号路径距地球在1 000 km以上)的信号.因此通过飞行器的概略位置、GNSS卫星的位置及地球的位置之间几何关系判断接收的信号是否可用，避免大气延迟误差Tj和Ij对测量精度的影响.

图1 高轨飞行器与GNSS卫星之间的相对位置

载波相位观测中的系统性残差将折合到N0j中，因此N0j的过程噪声的主要决定因素为卫星星历误差变化率和卫星钟差残差变化率.

卫星星历误差的变化率主要由各种未建模的摄动力决定，对定位精度的影响主要通过其在视线方向的分量来体现.可通过式(3)对星历误差变化率的影响进行保守估计.

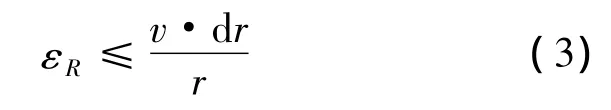
式中，r表示卫星到飞行器的距离;v表示飞行器的飞行速度;d r表示卫星的星历误差.对于高轨飞行器而言，信号可用的卫星到飞行器的距离大于4×104km，通过式(3)估算可得星历误差引起的变化率的量级约为1mm/s.另外，如果从IGS可获得实时预报的精密星历数据［10］，星历误差对N0j的影响将更小.

卫星时钟误差主要由星载原子钟的性能决定，变化非常缓慢，折合成距离约为1～2mm/s.

1.4 平方根滤波算法

为了避免计算机舍入误差对高精度的载波相位测量数据带来的影响，采用平方根滤波方法.又考虑到观测方程具有非线性特点，以及UKF相对于EKF的优越性能，决定采用平方根 UKF(SRUKF)方法进行信息融合.算法表述如下:

设非线性动力学系统可以写为:

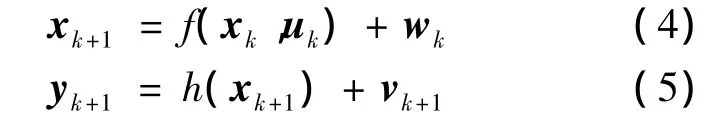
式中，x为n维状态向量;w和v均为白噪声，方差分别为Qw和Rν;假设x0和wk+1及vk+1互相独立.

1)初始化.

2)计算采样点.

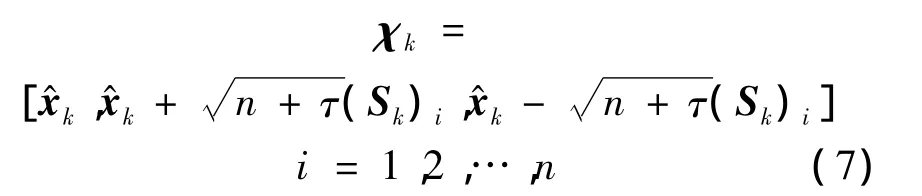
式中，n为状态维数;(Sk)i为Sk的第 i行;τ=α2(n+kc)－n，α为首要刻度因数，其一般取一个小于1的正常数;kc为第3刻度因数，通常取0.

3)时间更新

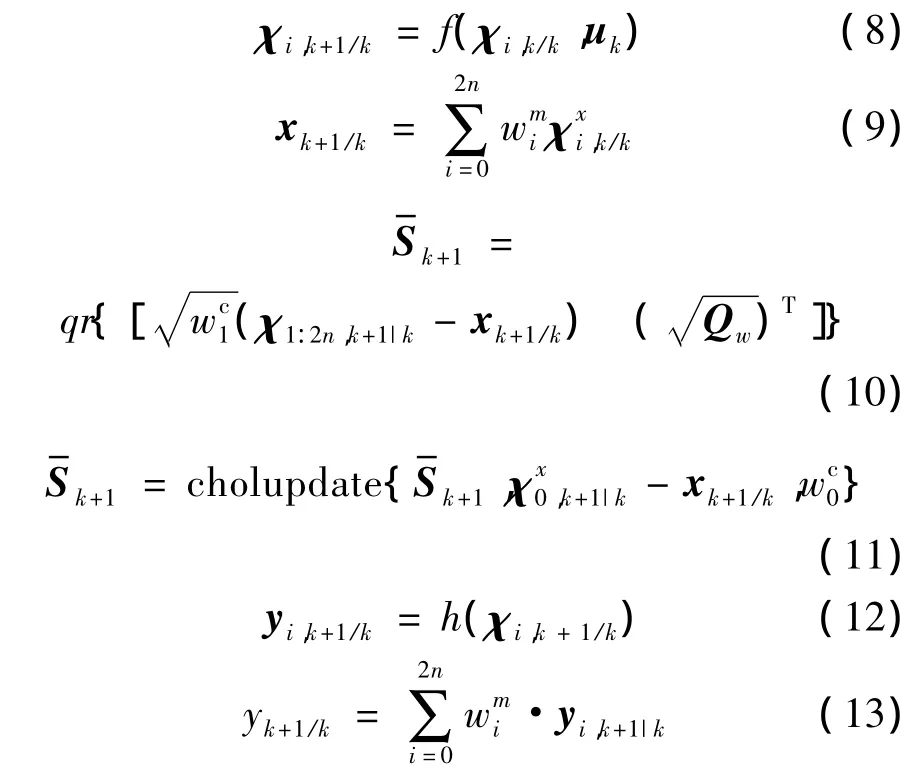
4)测量更新

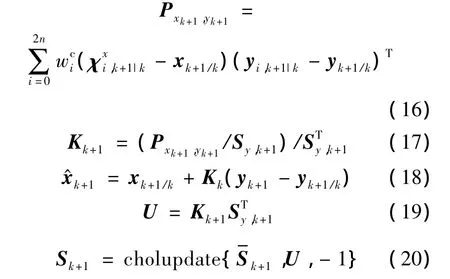
2 滤波器故障检测方法

只有可靠的导航系统才能保证飞行器正常工作，降低灾难发生的风险.捷联惯导通常可靠性较高，而且有备份和自检方法.并且考虑到在本研究中捷联惯导大部分时间段处于微重力环境下(除飞行器进行轨道机动的时段外)，加速度计测量信息不参与融合，因此对捷联惯导的故障检测方法在此不作研究.导航系统可能的故障源有:接收机在工作过程发生周跳、短时间内卫星时钟故障及广播的误差较大的星历数据等等.故障如不及时检测并隔离将导致滤波器发散，估计结果不可信.

对小故障或软故障的有效检测一直是滤波器故障诊断中的难点.因为观测数据发生小的故障或缓变故障时，观测数据在一定程度上还有使用价值，经过一段时间的积累才可能导致滤波器发散.本文提出基于整周浮点解交集的方法判断某颗卫星的载波相位测量信息是否导致滤波器发散.当某颗卫星对应的整周浮点解的交集为空集时，认为该颗卫星发生的故障已达到不可容忍的程度，应停止使用该颗卫星.当需要重新使用该颗卫星时，使用伪距对整周浮点解及其方差进行初始化.该方法在一定程度上提高了滤波器的鲁棒性.具体方法描述如下:

假设从t0时刻开始对卫星j进行观测，获得伪距 ρ0，从而获得整周模糊度的估计范围.在 t1时刻通过滤波器融合各种测量信息获得的估计值及其方差，从而获得其估计范围.令.在t2时刻通过滤波器融合各种测量信息获得的估计值及其方差，从而获得其估计范围.令.这样一直持续下去.若 Qtk= Φ，则说明该颗卫星有周跳故障，或滤波器发散，需要重新用伪距进行的初始化.

3 计算机仿真与分析

基本仿真条件:飞行器从高度200 km的停泊轨道出发沿高偏心率椭圆轨道飞向地球同步轨道，飞行器在惯性坐标系J2000内的初始位置和速度分别为5815.282 km，3059.500 km，0.00 km，7.2 km/s，7.2 km/s，0.0 km/s，总飞行时间为16300 s，最终飞离地球的高度为40 038 km.飞行过程中飞行器在900～1 100 s，5 400～5 600 s和15900～16100 s进行了轨道机动，发动机产生的加速度大小为0.25m/s2.观测卫星有GPS，GLONASS，GALILEO，BEIDOU2.各类卫星信号相对于地球的张角分别为 ±21.3°，±21.3°，±12.2°和±8.6°.星历误差 0.2 m，卫星钟差等效距离1.5m［10］.伪距测量精度为 15 ～30m.载波相位测量噪声均方差为0.01周.接收机测量信号的频率为1Hz，能接收的信噪比(C/N0)dB阈值为18 dBHz.在轨道机动前，使用自带星敏感器对捷联惯导进行初始对准，对准精度为20″.导航卫星的可见性依据是否在主瓣信号信的覆盖区域及信号的信噪比是否大于接收机的最低门限值来确定.陀螺测量精度约为0.02(°)/h，加速度计测量精度约为1×10－3g0.GNSS卫星的可见性如图2所示.

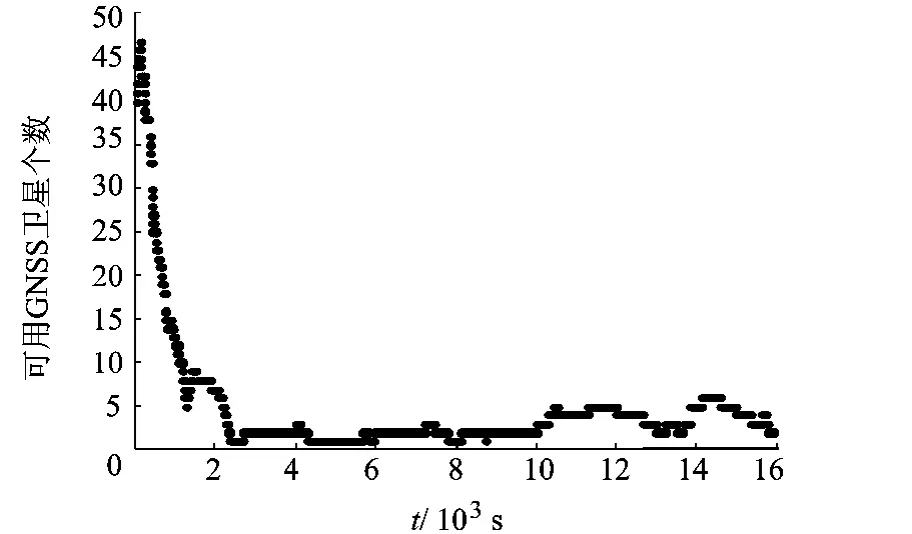
图2 飞行器飞行过程中可用卫星的颗数

载波相位/捷联惯导组合对飞行器进行导航结果如图3和图4所示.图中eR表示实际定位误差，“3σR”表示定位误差的3倍均方差;eV表示实际定速误差，“3σV”表示定速误差的3倍均方差.

从仿真结果可得:当飞行器处在高轨段，绝大部分情况下，可用的GNSS卫星数量少于4.随飞行器的高度增加，定位精度越来越差.这主要是因为飞行器上的接收机只能使用地球对面的卫星信号，导致相应的几何结构逐渐变差.由于捷联惯导测量误差的引入，导致在飞行器机动过程中定位定速均方差迅速增大.在轨道高度为40 038 km处，使用载波相位/捷联惯导组合可使的飞行器定位均方差达到51m，定速均方差达到0.149m/s.

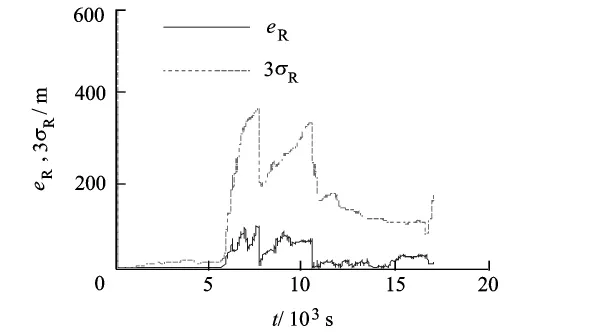
图3 载波相位/捷联惯导组合对高轨飞行器定位结果

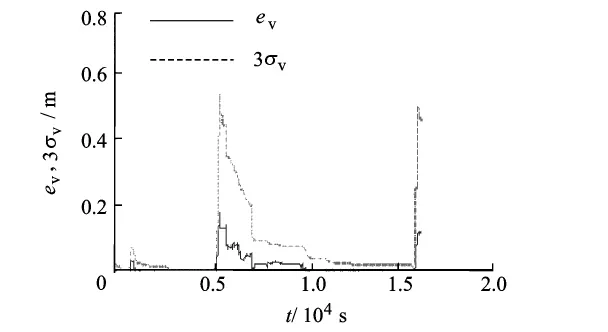
图4 载波相位/捷联惯导组合对高轨飞行器定速结果

4 结论

本文基于卫星载波相位/捷联惯导组合为高轨机动飞行器设计了一种新的自主导航方案.对误差特性的准确分析是提高导航精度的基础.在文中将载波相位的整周浮点解作为状态变量进行估计，充分利用了载波相位的高精度测量信息和测量方程中系统性误差缓变的特点，获得了较高的导航精度.

提出基于整周浮点解区域交集检测滤波器是否正常的方法.该方法通过对整周模糊度状态的检验，判断微弱故障积累是否导致滤波器发散，通过整周模糊度状态的初始化可避免滤波器的发散，从而使导航方案同时具有高精度与高可靠性的特点.

如果能合理使用伪距、载波相位、捷联惯导及天文等多种测量信息，设计合理的组合导航系统结构将会获得更高精度和更可靠的导航系统.研究结论对提高我国空间飞行器的自主生存能力、高轨飞行器交会对接及导航星座维护等方面具有一定价值.

References)

［1］ PsiakiM L，Jung H.Extended Kalman filter methods for tracking weak GPS signals［C］//Proceedings of the Institute of Navigation GPS 2002.Portlan:［s.n.］，2002:2539 －2553

［2］ Michael C，Davis E P，Carpenter JR.Results from the GPS flight experiment on the high earth orbit AMSAT oscar-40 spacecraft［C］//Proceedings of the Institute of Navigation GPS 2002 Conference.Oregon:［s.n.］，2002:122 －133

［3］ PalmeriniG B，Sabatini M，Perrotta G.Enroute to the Moon using GNSS signals［J］.Acta Astronautica，2009，64:467 －483

［4］ Gwanghyeok Ju，Keunjoo P A R K，Sang-Ryool LEE.GNSS-based satellite navigation strategy for geosynchronous orbit and Trans-Lunar orbit［C］//60th International Astronautical Congress 2009，2009

［5］范利涛，汤国建，吴杰.基于GPS对地球同步轨道自动转移飞行器进行导航的可行性分析［J］.空间科学学报，2008，28(4):311－315 Fan Litao，Tang Guojian，Wu Jie.Feasibility of geosynchronous ATV navigation based on GPS［J］.Chin JSpace Sci，2008，28(4):311－315(in Chinese)

［6］ Fan Litao，Zheng Wei，Tang Guojian，et al.Autonomous navigation method for orbital maneuver vehicle based on square-root unscented Kalman filter［J］.Journal of Chinese Inertial Technology，2008，16(6):687 －693

［7］秦红磊，梁敏敏.基于GNSS的高轨卫星定位技术研究［J］.空间科学学报，2008，28(4):316 －325 Qin Honglei，Liang Minmin.Research on positioning of high earth orbital satellite using GNSS［J］.Chin JSpace Sci，2008，28(4):316－325(in Chinese)

［8］柳丽，董绪荣，郑坤，等.星载GNSS确定GEO卫星轨道的积分滤波方法［J］.中国空间科学技术，2011(1):70－74 Liu Li，Dong Xurong，Zheng Kun，et al.Integral filter method of orbit determination for geostationary satellite based on spaceborne GNSS［J］.Chinese Space Science and Technology，2011(1):70－74(in Chinese)

［9］赵雯雯，张立新，蒙艳松，等.全球导航星座的远地/深空导航应用研究［J］.中国科学:物理学力学天文学，2011，41(5):581－588 Zhao Wenwen，Zhang Lixin，Meng Yansong，et al.The application research of global navigation constellation for HEO(high earth orbit)satellites and deep-space satellites［J］.Sci Sin Phys Mech Astron，2011，41(5):581 －588(in Chinese)

［10］ Misra P，Enge P.Global positioning system signals，m Measurements，and performance，second edition［M］.Beijing:Publishing House of Electronics Industry，2008:181 －211

(编 辑:张 嵘)

Carrier phase/SINS integrated navigation for spacecraft on high earth orbit

Wen Yongzhi Wu Jie
(College of Aerospace and Material Engineering，National University of Defense Technology，Changsha 410073，China)

Because of the fewer available satellites and the greater wastage of signal on space link，the measurement accuracy is lower using pseudo-distance.The method of autonomous navigation using carrier phase of global navigation satellite system(GNSS)and strapdown inertial navigation system(SINS)was presented for the high earth orbitautomotive spacecraft.The float solutions of initial integer ambiguity were used as states variable in this method，and the nonlinear filter was established by square-root unscented Kalman filter(SRUKF).The method of cycle slips faults detection and isolation was presented based on the intersections of the float solutions.The method of integrated navigation makes full use of the high measurement accuracy of carrier phase and slowly varying characteristic of systematic errors，and it can increase the reliability and the precision of the navigation system.

carrier phase;strapdown inertial navigation system(SINS);integrated navigation;fault detection and isolation

V 249.32+3

A

1001-5965(2012)06-0726-05

2011-03-03;网络出版时间:2012-06-15 15:43

www.cnki.net/kcms/detail/11.2625.V.20120615.1543.018.htm l

温永智(1983 －)，男，河南新乡人，博士生，wyzgfkd@yahoo.com.cn.