基于“魂芯一号”的自适应截位浮点乘法实现∗

(中国电子科技集团公司第三十八研究所,安徽合肥230088)

0 引言

在雷达阵列信号处理算法中,很多计算权系数的过程中都要用到自相关矩阵的求逆[1],但是由于自相关矩阵具有较大的条件数,为了保证求逆过程的准确性,必须要求自相关矩阵具有较高的精度[2]。现阶段32位单浮点精度无法满足自相关浮点矩阵的精度要求,因此本文基于国产“魂芯一号”DSP(简称BWDSP100)的指令系统,提出了一种自适应截位的浮点复数矩阵乘法,将浮点数据以最大值为基准扩位成定点数据,采用BWDSP100指令集中的72位定点乘累加器,将乘累加后的结果通过自适应截位处理,并对获取浮点数据的指数位进行调整,使得最终获取的结果最大程度地保留小数精度,减少截位过程的误差影响。

本文使用BWDSP100作为实现平台,BWDSP100是由中国电子科技集团公司第三十八研究所研制,可广泛运用于各种高性能计算领域,如雷达、电子对抗、精确制导、通信保障、图像处理等信号处理领域。作为BWDSP系列的第一款产品,BWDSP100是一款32位浮点DSP,同时兼容16位和32位定点数据格式,采用VLIW架构,具有强大的并行处理能力,能较好地满足高速实时信号处理的应用要求[3]。

1 算法的实现流程

1.1 单精度浮点算法存在的问题

对于雷达信号处理中的自相关矩阵而言,在求取过程中R=A∗A′,其核心运算由大量的浮点乘累加运算构成。而根据IEEE标准754/854,如图1所示,32位单精度浮点格式包含一个符号位s、一个24位的尾数和8位无符号量指数e[4]。

对于原始矩阵的数据,当其动态范围较大时,在进行乘累加运算的过程中,有可能导致个别数据的小数位被舍弃,最终导致误差结果的累积。

同时,普通的浮点乘法运算存在截位舍去问题。在进行32位浮点乘法运算过程中,其运算过程如图2所示。

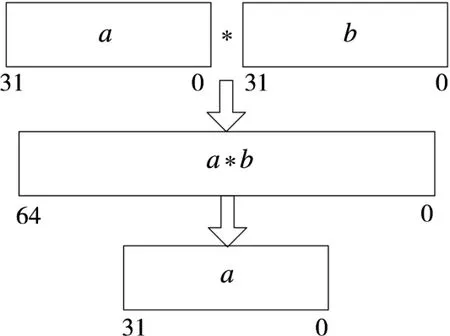
图2 正常32位浮点运算流程

处理器在进行32位浮点乘法的过程中,需要对生成的数据进行截位,从而输出32位的浮点数据结果,在截位的过程中会导致数据的偏差[5]。该误差在一次的浮点运算中没有明显的体现,但是在工程实践中进行自相关复数矩阵的运算过程中,误差被累积放大,导致后续运算无法进行。

1.2 本文算法的实现

为了在最大程度上保留浮点的运算精度,且充分发挥BWDSP100指令集中72位定点乘累加器的作用,首先按照一定的规则将原始浮点数据转化为定点数据[6],然后采用BWDSP100的指令系统进行定点的乘累加运算,最后再把求取的定点乘累加结果转化为所需要的浮点数据。其具体的转化步骤如下,流程图如图3所示(以矩阵F=[fij]24∗80为例)。

算法的具体流程为:

1)对输入复数矩阵,按行不区分实虚部取最大值EXP(矩阵EXP=[expij]24∗1);

2)以步骤1)中取得的最大值为基准,将浮点数据扩位为32位定点数据,此时获取定点矩阵A(矩阵A=[aij]24∗80);

3)在进行自适应相关矩阵运算时,需要对复数矩阵进行共轭转置,即得到矩阵B(矩阵B=[bij]80∗24);

4)对于矩阵乘法而言,由于是A∗B,因此要进行576(即24∗24)次乘累加运算。对于BWDSP100的指令系统,采用72位乘累加器MACC进行上述乘累加运算,获取MACC的值;

5)对于每次获取的72位MACC,从最高位开始判断符号位的位数,然后从符号位开始截32位,最大程度保留运算过程的低位数据;

6)将截取的32位定点数据转化为浮点,然后根据数据截位以及原始扩位的位数,对浮点数据的指数位进行修正,得到结果CO(矩阵CO=[coij]24∗24)。

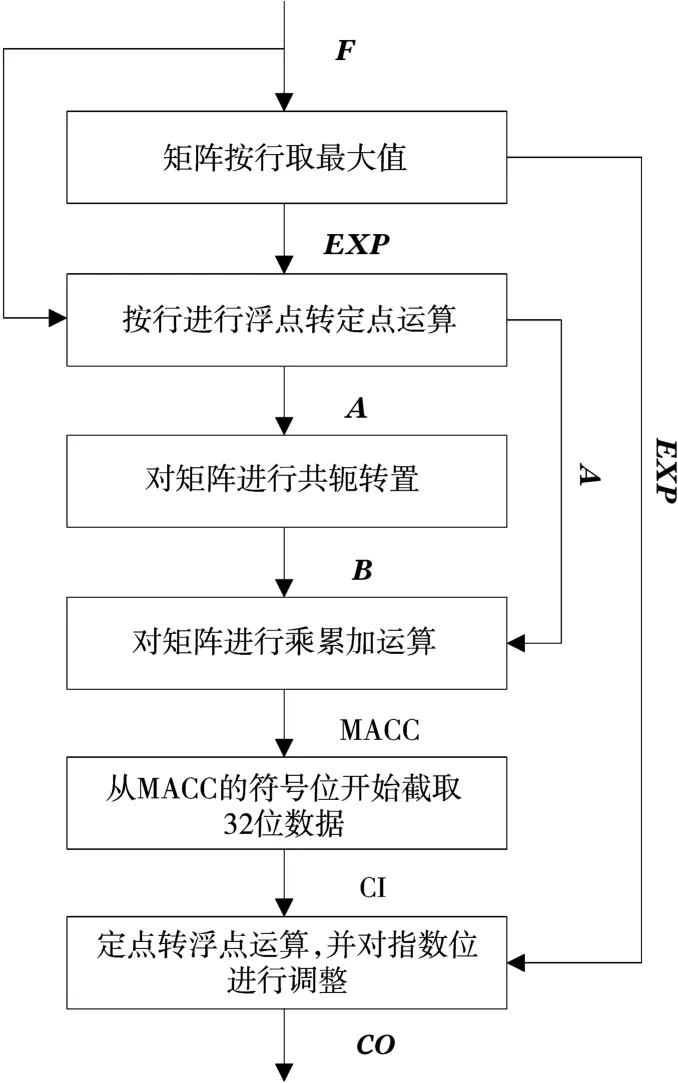
图3 浮点转定点矩阵乘法的流程图

1.3 自适应截位处理

对于上述算法流程而言,在最大程度上保留计算精度的前提下,如何将72位乘累加器中的结果通过BWDSP100指令系统转化为32位浮点数据是本文的关键。

对于一个BWDSP100中的72位乘累加器而言,其具体的表示如图4所示[7]。

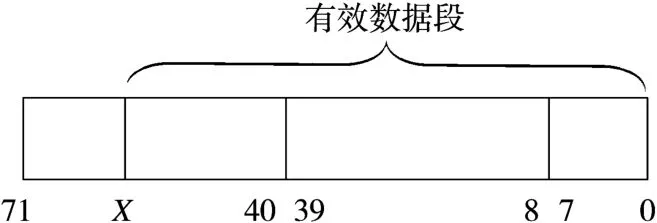
图4 72位定点乘累加器MACC的数据表示

如图4所示,由于MACC是由若干个32位定点数(其中最大值为满32位)进行乘累加运算而得到,故X表示的位数一定介于63～71之间,为了从中截取32位数据长度且最大程度的保留精度,因此需要将其中的[X-32∶X]位截取出来,这就需要对X的位数进行判断获取,然后基于BWDSP100的指令系统,进行具体的截取操作。下面是处理的主要流程:

1)由于数据符号位的判断需要在寄存器堆中进行,因此需要将72位的MACC数据放置到若干寄存器中。为了简化运算,降低8位截掉,只将MACC中[71∶40]与[39∶8]分别放置到两个寄存器中去,如图5所示。

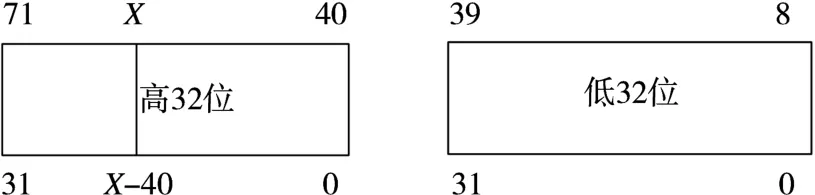
图5 将MACC通过截位放置到寄存器中

在截位的过程中,需要对数据进行四舍五入处理。当截掉的最高位为1时,则在保留的最低位上加上1,减少截位误差的影响。

2)现在要从64位数据中截取32位数据以最大程度地保留精度,因此要判断其最高的有效位在多少位,如图5中X的取值。

基于BWDSP100指令集中的pos1指令,该指令给出寄存器中1对应的最高位置,根据该位置,高32位寄存器左移相应位数,低32位右移相应位数(均是逻辑移位),然后再进行“与”操作。

3)最后将定点数据转化为浮点,并对浮点数据的指数位进行相关调整,一方面考虑最初浮点转定点的扩展位数,还要考虑MACC的截位以及步骤2)中的移位,根据BWDSP100指令集中的exp与fext指令对其指数位进行调整。

根据上述步骤,能够在最大程度上保留乘累加过程中的尾数部分,防止由于数据截位导致的误差,其具体的流程图如图6所示。

图6 乘累加器MACC的自适应截位流程示意图

2 实验结果

采用若干组实际的某型号雷达波束数据经过FFT运算后形成的复数矩阵进行测试,分别采用TS201的浮点复数矩阵乘法、BWDSP100的浮点复数乘法和本文算法进行计算,并将结果与MATLAB计算的标准结果进行对比,如表1所示。

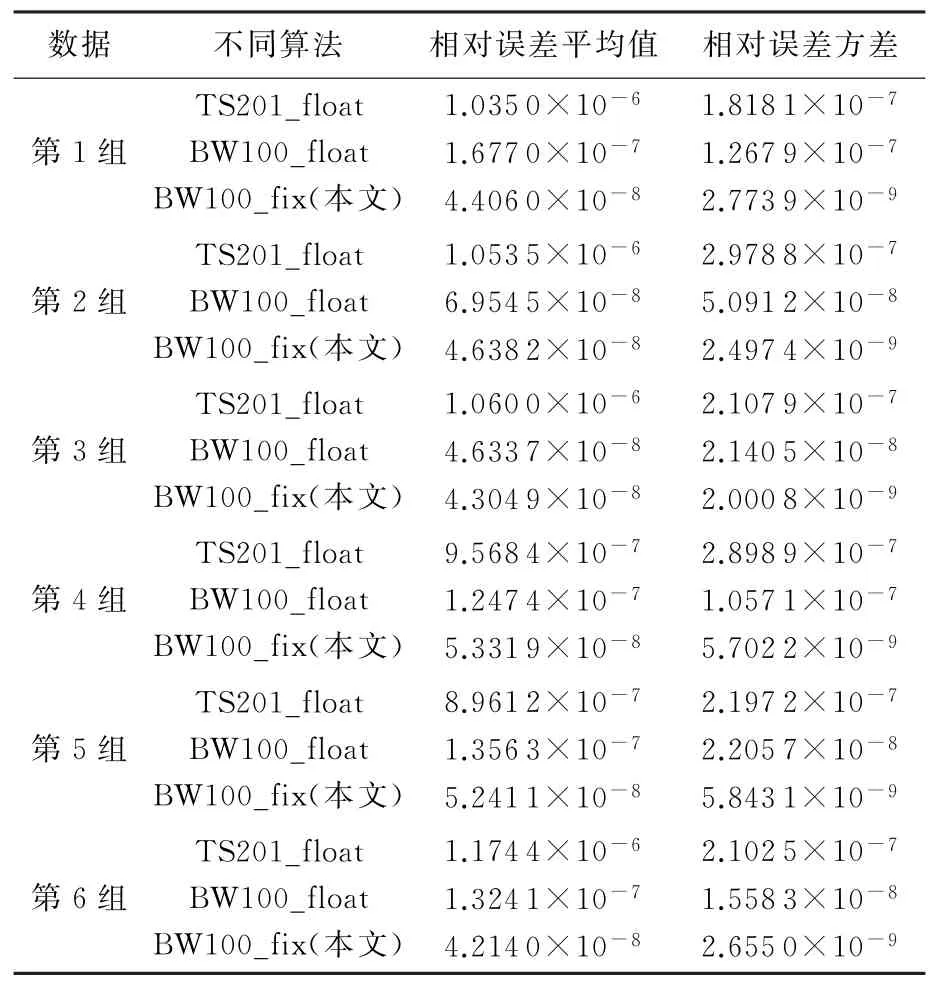
表1 不同算法数据与标准MATLAB的误差和方差分布

根据表1中的误差对比可以看出,本文算法在整体上能够有效提高运算精度,与BWDSP100的浮点算法相比能够提高一个数量级,与TS201的浮点算法相比甚至能够提高两个数量级,同时在误差分布上也具有很大的优势。选取其中两组数据绘制三维分布图能够更加明显地看到上述结论,如图7、图8所示。

图7 第1组数据的相对误差分布图

3 结束语

目前浮点算法运算精度上的不足,导致部分需要高精度浮点运算结果的算法无法实现。本文在BWDSP100指令系统的基础上,提出了一种自适应截位的浮点转定点浮点复数乘法的新算法。仿真结果表明,本文提出的新算法能够有效提高浮点运算的精度,降低误差分布,与普通的浮点算法相比具有较明显的优势。最终应用到某型号雷达中,其检测效果实现了明显提高。

[1]ELGAMEL S A,SORAGHAN J J.Enhanced Monopulse Radar Tracking Using Filtering in Fractional Fourier Domain[C]∥2010 IEEE International Radar Conference,[S.l.]:[s.n.],2010:247-250.

[2]SKOLNIK M I.雷达系统导论[M].3版.左群声,徐国良,马林,等译.北京:电子工业出版社,2006:56-62.

[3]中国电子科技集团公司第三十八研究所.BWDSP100软件用户手册[M].合肥:中国电子科技集团公司第三十八研究所,2011.

[4]ARANDI S,EVRIPIDOU P.Programming Multi-Core Architectures Using Data-Flow Techniques[C]∥2010 International Conference on Embedded Computer Systems,Samos:IEEE,2010:152-161.

[5]史鸿声,穆文争,刘丽.基于“魂芯一号”的雷达信号处理机设计[J].雷达科学与技术,2012,10(2):161-164.SHI Hong-sheng,MU Wen-zheng,LIU Li.Design of Radar Signal Processor Based on HunXin-1 Chip[J].Radar Science and Technology,2012,10(2):161-164.(in Chinese)

[6]黎渊,蒋江,张选民,等.基于模拟退火算法的浮点转定点自动位宽优化工具[J].上海交通大学学报,2013,47(1):76-85.

[7]龚晓华,郭二辉,刘小明.BWDSP100高速链路口模块的设计[J].中国集成电路,2012(3):60-64.