中国粮食价格波动的ARCH效应研究

毛 伟，赵新泉

（1.中南财经政法大学统计与数学学院，武汉430073；2.广东海洋大学经济管理学院，广东湛江524088）

0 引言

一些市场特别是金融市场，由于易受谣言，政府的财政政策和货币政策，政局波动的影响，使得市场中的某些时间序列具有波动集群性的特征。粮食是一种与国计民生息息相关的重要商品，近年来，中国粮食价格波动频繁，且出现价格不断上升的态势，这必然引起其它部门生产成本和产品产量的波动，从而对中国国民经济的正常运行造成不利影响。ARCH类模型较好地解决了时间序列中的异方差问题，因而被广泛应用于金融市场的研究中，使用这类模型来研究中国粮食市场粮价波动的特征及原因，对我国粮食价格的稳定和粮食市场的健康发展具有重要的现实意义。

本文拟依据ARCH类模型均值方程残差不同分布的假设，对粮食价格的波动的特征进行分析，主要验证以下几个问题：①残差分布的假设是否对模型结果产生重大影响？②在合适的残差分布假设下，何种ARCH类模型更适合分析中国粮价波动的特征？③粮食价格波动是否具有集簇性？④粮食价格波动是否具有非对称性或高风险高回报的特征？⑤粮食价格波动的主要原因来自与粮食系统内部还是外部？

1 模型与方法简介

本文首先对价格波动率序列进行单位根平稳性检验，其次借助ARMA模型来设定均值方程并对其进行ARCH-LM检验，然后对均值方程的残差进行正态分布检验，说明假定残差服从正态分布并不是一个好的选择，最后分别在三种残差分布（正态分布、学生t分布和GED分布）下建立ARCH类模型，并进行比较分析。

1.1 ARCH类模型

1.1.1 对称的ARCH类模型

（1）GARCH模型。GARCH模型由Bollerslev(1986)提出，该模型解决了当用ARCH模型描述某些时间序列时，ε2t的滞后项过多的问题，模型形式如下：

式（1）被称为均值方程，式（2）被称为方差方程，一般要求 p≥0,q＞0；αi≥0,i=0，1,…,q；β≥0,j=1,…,p。分别为ARCH项和GARCH，若它们两者都高度显著，则表明粮价的收益率的波动集簇性显著。一般地，GARCH（1，1）就可描叙很多有异方差的时间序列。

（2）GARCH－M模型。在GARCH模型的均值方程（1.1）中加入条件标准差ht（或用条件方差ht2代替，或用条件方差ht2的对数值代替），方差方程不变，就变成了GARCH－M模型：

条件标准差代表了期望风险的大小，参数λ是可测的预期风险波动对Rt的影响程度，它代表风险和收益（或波动）之间的一种权衡，依据该参数符号就可以辨别出中国粮食市场是否存在高风险高回报的现象。

1.1.2 非对称的ARCH模型

（1）TARCH模型。其条件方差方程为：

其中ut≥0表示利好消息，ut＜0表示利坏消息，于是，利好和利坏消息对条件方差造成了不同的影响：好消息有一个α倍的冲击，坏消息有一个（α+φ）的冲击。若φ≠0，条件方差对冲击的反应是非对称的，称这种现象为杠杆效应。所以，可以从φ的符号辨别出中国粮食市场上，价格上涨信息和价格下降信息两者之间是谁引发的粮价波动更大。

（2）EGARCH模型。其条件方差方程为：

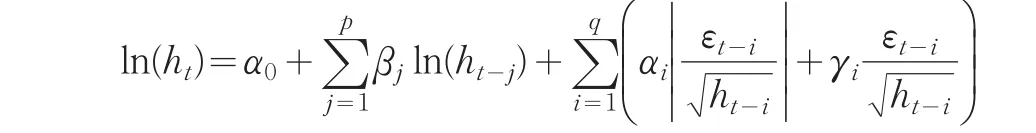
总之，GARCH类模型将本期波动的来源分为两部分：变量前期的波动和前期的外部冲击，αi反应经济变量前期外部冲击对本期波动的影响，βj反映经济变量过去的波动对本期波动的影响。如果αi与βj大于零且显著，则说明序列有显著的波动集簇性。

1.2 GARCH模型的扰动项分布假设

实践中，很多时间序列尤其是金融时间序列的无条件分布往往具有比正态分布更宽的尾部，为更精确地描述尖峰厚尾特征，有必要对误差项的分布进行假设，通常，GARCH模型扰动项的分布有3种假设：正态分布、学生t分布和GED分布。它们的密度函数依次为：

（1）标准正态分布，它是ARCH类模型的标准化残差序列最常采用的分布假定，其密度函数为：

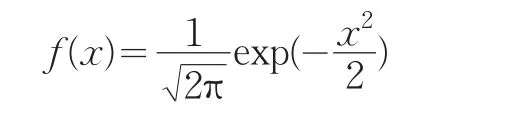
标准正态分布意味着信息冲击在整个期间内是均匀分布的。

（2）t分布，它是对称分布，其均值为0，当自由度n→∞很大时，它趋近与正态分布。通常，t分布的概率密度比正态分布有更厚的尾部和更尖的顶部。t分布的密度函数为：，其中n是自由度。

(3)广义误差分布（GED），其概率密度函数如下：

P是分布中唯一的一个参数，当p=2时，GED分布退化为标准正态分布；当p＜2时，相对于正态分布，其分布具有更厚的尾部，更尖的峰，而且p值越小，尖峰厚尾现象越明显；当p＞2时，其尾部较正态分布就更薄。

2 数据描述性统计分析

2.1 数据来源

粮食批发价格指数反映了粮食市场的某些特征，本文采用粮食批发价格指数的周数据来研究我国粮食市场的波动特征，样本区间为2004年1月4日至2009年8月9日，共得到293个周的数据。记粮食批发价格指数为Pt（t=1，2，…，350），这里Pt表示从2004年4月11日起第t周的价格指数。价格指数的周波动率R用相邻周粮食批发价格指数的对数一阶差分表示，即:Rt=1nPt-1nPt-1。数据来源于中国粮网(http://www.Cngrain.com)。本文使用Eviews6.0和SPSS19.0来进行分析。

2.2 粮食价格指数周波动率的基本统计特征

单位根平稳性检验结果表明，价格指数的周波动率序列平稳。观察周波动率序列的自相关图和偏自相关图，并根据AIC信息准则和SC信息准则，经过反复比较，最终确定均值方程为ARCH-LM检验表明：周波动率序列存在至少10阶的ARCH效应。

2.3 均值方程残差的正态分布检验

对均值方程的残差的正态分布进行检验，检验结果如表1所示

表1 均值方程残差序列的基本统计量

由表1可知，玉米均值方程残差的偏度为－1.016923，说明其分布曲线左边拖着较正态分布长的尾巴；峰度大于3，说明其分布曲线尾部较正态分布粗壮且顶端更尖，其Jarque-Bera统计量也远大于5%显著性水平上χ2(2)的临界值，因而拒绝残差是分布正态的假设。

从残差序列分布直方图（图1）和QQ散点图（图2）可见，残差分布呈现出“尖峰厚尾”的特征，相对于标准正态分布，其顶端更高更尖，尾端更厚，如果假定其服从正态分布，拟合效果较差。图2中的QQ散点图进一步说明了正态分布并不适合用于描述均值方程的残差序列。

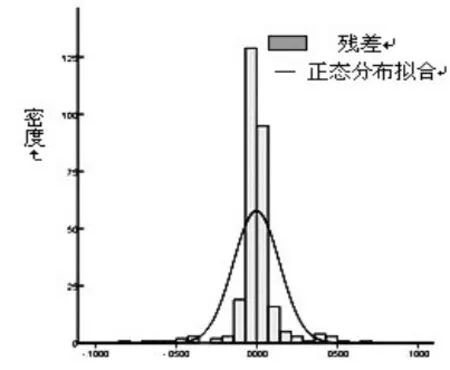
图1 正态分布密度拟合图

图2 正态分布QQ散点图

3 均值方程残差序列的分布对ARCH类模型结果的影响

考虑到建模的简洁性和显著性，下面分别运用非对称ARCH类模型和对称ARCH类模型，即TGARCH（1，1）、EGARCH（1，1）和GARCH（1，1）、GARCH-M（1，1）模型，并分别在三种不同残差的分布（正态分布、学生t分布和GED分布）的假定下建立模型，并比较各个模型的拟合结果。

ARCH-LM检验表明所建模型的ARCH效应已消失，残差之间独立性较强。为了确定中国粮食市场是否存在杠杆效应，好坏信息对粮食市场的冲击效果是否不同，首选使用TARCH和EGARCH模型对波动率序列进行分析，模型的估计结果如下（详见表2）：

表2 非对称ARCH类模型在三种分布下估计结果

（1）从非对称ARCH类模型的拟合程度看，假定残差服从t分布时，模型的AIC值和SC值最小，且对数似然值最大，这表明t分布能更好地拟合均值方程的残差序列，其次是GED分布，正态分布的拟合程度最差。

（2）与采用t分布和GED分布拟合残差相比，采用正态分布去研究中国粮食价格波动是否存在杠杆效应的问题时，模型得出的结论相反：假定残差服从t分布和GED分布时，TARCH模型中φ的估计值大于零，在EGARCH模型中，γ的估计值小于零，但它们分别在5%水平和10%水平下不显著，这说明，中国粮食价格波动没有显著的非对称性，粮食市场中价格上涨信息引发的波动与价格下跌信息引发的波动相比并无明显区别；而假定残差服从正态分布时，TARCH模型中φ的估计值大于零，EGARCH模型中γ的估计值小于零，且它们都在5%水平下显著。这说明，粮食市场中价格上涨信息引发的波动比价格下跌信息引发的波动要小，中国粮食价格波动具有显著的非对称性。

（3）不同残差分布下，均值方程的形式不同。当残差服正态分布时，无论是在TARCH，还是在EGARCH模型中，εt-2项对当期粮食价格的波动率的影响从t分布和GED分布时的显著变成了不显著。

与假定残差服从正态分布的模型相比，残差服从t分布和GED分布时模型的拟合程度更好，这表明假定残差服从正态分布时，ARCH类模型描述粮食波动率结论的准确性值得怀疑。

下面使用对称ARCH类模型来进行分析，并利用GARCH－M模型来检验粮食市场的波动率与风险的关系，模型的估计结果如下（见表3）：

（1）从对称ARCH类模型的拟合程度看，假定残差服从GED分布时，模型的AIC值和SC值最小，且对数似然值最大，这表明GED分布能更好地拟合均值方程的残差序列，其次是t分布，正态分布的拟合程度最差。

（2）不同分布下，模型参数约束条件满足情况有差异。当残差服从GED分布时，GARCH和GARCH－M模型的GARCH项都近似为零，但都不显著，ARCH项大于零，且在5%的水平下显著，它们不仅满足参数约束条件，而且表明粮食价格波动率序列具有显著的波动集簇性，即较大的价格波动后面伴随着较大的波动，较小的价格波动后面伴随着较小的波动；当假定残差服从正态分布和t分布时，GARCH和GARCH－M模型的GARCH项都小于零，且显著，这不满足GARCH类模型的平稳性约束条件,表明它们二者并不适合分析中国粮价波动问题。

（3）不同分布下，模型系数的显著性差异较大，从而导致模型各系数对粮食波动率的影响产生了变化。假定残差服从GED分布时，GARCH和GARCH－M模型的均值方程系数估计值均在1%的水平下显著，这两个模型的GARCH项都接近零，但都不显著，它们方差方程中其余各项都在5%的水平下显著；假定残差服从正态分布和t分布时，GARCH和GARCH－M模型的均值方程系数估计值均不显著。除t分布下GARCH－M模型的GARCH项在10%的水平下显著外，方差方程中ARCH项和GARCH项都在1%的水平下显著。

表3 对称ARCH类模型在三种分布下估计结果

（4）不同残差分布下，研究中国粮食市场是否存在高风险高回报的特征的问题时，模型得出的结论不同。GED分布下，均值方程中λ估计值为0.14，且在1%的水平下高度显著，表明当市场中的预期风险增加一个单位时，就会导致粮食价格指数周波动率也会相应地增加0.14个百分点，这反映了粮食市场存在高风险高回报的特征；而在正态分布和t分布下，λ估计值均不显著，表明粮食市场并不存在高风险高回报的特征。

总的来说，无论是用对称ARCH类模型，还是利用非对称ARCH类模型，假定残差服从正态分布时，模型的拟合程度是最差的，因此所得出的结论的准确性也应该是最差的。t分布下，EGARCH模型的AIC值和SC值最小，且对数似然值最大，表明在这四种模型和三种残差分布中，残差基于t分布的EGARCH模型的拟合程度最高。

4 结论

本文对正态分布、t分布和正态分布下的ARCH类模型结果进行了对比，发现不同的分布具有不同的结果。由于均值方程的残差序列并不服从正态分布，并且t分布和GED分布下，模型的拟合程度更高，因此当我们利用假定残差服从正态分布的ARCH类模型来描述粮食价格的波动率时，所得出结论的准确性是值得怀疑的。相同条件下，假定残差服从t分布和GED分布的ARCH类模型所得结论的可信度要更高一些，由此得出以下结论：①中国粮食价格波动没有显著的非对称性，好坏信息对粮食市场的冲击效果并无明显区别。②粮食价格波动率序列具有显著的波动集簇性。③粮食市场存在高风险高回报的特征。

结合中国的粮食市场的实际情况，模型估计结果表明：①好坏信息对粮食市场的冲击效果无明显差别，这表明中国政府对粮价波动问题非常重视，采取的调控措施比较得当。②GED分布下，GARCH和GARCH－M模型的GARCH项都近似为零，但都不显著，这说明我国当期粮价波动受前期粮价波动的影响并不是引起我国粮价波动的主要原因。它们的ARCH项大于零，且在5%的水平下显著，说明我国粮价当期的波动的主要原因是前期粮食市场系统以外的因素波动的冲击，这些外部因素包括交易人的心理因素，宏观经济情况和物价等因素。③粮食市场存在高风险高回报的特征，这表明中国粮食市场的大部分交易者在做决策时理性因素大于非理性因素，在政府对粮食市场的监控和引导之下，中国粮食市场已逐渐向趋于合理和成熟的道路发展。

除了用t分布和GED分布来刻画残差的尖峰厚尾特征以外，描叙尖峰厚尾特性的分布有很多，如何体现其“有偏”特性，并将“有偏”和“尖峰厚尾”特征有机融合起来，提高模型估计精度，以便更恰当地描述中国粮食市场价格的波动率，是下一步研究的方向。

[1]罗万纯，刘锐.中国粮食价格波动分析：基于ARCH类模型[J].中国农村经济,2010,(4).

[2]卢方元，李成钰.不同分布对ARCH类模型结果的影响－基于上证指数收益率的对比分析[J].数量经济技术经济研究,2007,(8).

[3]唐齐鸣，陈健.中国股市的ARCH效应分析[J].世界经济,2001,(3).

[4]何晓英.我国粮食价格上涨的原因及中长期走势分析[J].宏观经济管理,2011,(8).

[5]张娉研，柳欣.我国退货膨胀与粮食价格的实证研究[J].经济问题, 2011,(3).

[6]谭江林，罗光强.粮食价格波动与通货膨胀关系的实证研究[J].价格月刊,2009,(3).

[7]冯云.中国粮食价格波动的实证分析[J].价格月刊,2008.(2).

[8]Bollerslev,T.Generalized Autoregressive Conditional Heteroskedas⁃ticity[J].Journal of Econometrics,1986,(31).

[9]Nelson,D.B.Conditional Heteroskedasticity[J].Journal of Economet⁃rics,1991,(59).

[10]Lapp,J.S.,Smith,V.H.Aggregate Sources of Relative Price Variability among Agricultural Commodities[J].American Journal of Agricultur⁃al Economics,1992,(74).