基于相容粗糙集的ELM网络结构选择

翟俊海， 邵庆言， 苗 青

（河北大学 数 学与计算机学院，河北 保 定 071002）

0 引 言

粗糙集理论［1］是波兰数学家Pawlak教授于1982年提出的一种数据挖掘方法，已成功应用于数据挖掘、模式识别、机器学习及决策分析等领域。粗糙集理论是一种不确定性数据分析工具，与经典集合论、模糊集理论并称三大集合理论［2］。

Pawlak建立的粗糙集模型是架构在等价关系基础上的，用一对逼近算子（上近似算子和下近似算子）逼近目标概念。在逼近目标概念时，不需要任何先验知识，所以经典粗糙集模型是一种完全数据驱动的方法。但经典粗糙集模型只能处理离散值数据，使其应用有一定的困难。许多研究人员从不同的角度对经典粗糙集模型进行了扩展［3－12］。在允许有一定错分率的情况下，文献［3］提出了变精度粗糙集模型。文献［4－5］通过在经典粗糙集模型中引入概率方法，提出了概率粗糙集模型。文献［6］通过将决策理论引入到经典粗糙集，提出了决策粗糙集模型。这3种扩展模型是在等价关系的框架下，只对上近似算子和下近似算子的定义进行了改进。文献［7］将等价关系扩展为一般二元关系，提出了广义粗糙集模型。文献［8］将等价关系扩展为优势关系，提出了基于优势关系的粗糙集模型。文献［9］将等价关系扩展为相容关系，提出了相容粗糙集模型。在这3种扩展模型中，被逼近的目标概念和经典粗糙集是一样的，但将等价关系进行了扩展。文献［10］将被逼近的目标概念扩展为模糊集，等价关系扩展为模糊相似关系，提出了模糊粗糙集模型。相容粗糙集模型和模糊粗糙集模型均可以处理实值数据库。文献［11］对近年来国内外粗糙集理论研究的现状进行了综述，并讨论了当前粗糙集理论的热点研究领域以及将来需要重点研究的主要问题。

ELM（Extreme Learning Machine）是用于训练单隐含层前馈神经网络（Single－hidden Layer Feed－forward Network，简称 SLFN）的学习算法［12－13］。不同于反向传播算法（如 BP算法），ELM算法不需要反复迭代，它随机生成输入层到隐含层的权值和偏置，然后用分析的方法确定隐含层到输出层的权值。近年来，ELM已成为神经网络领域的一个研究热点，引起了众多研究人员的兴趣，并成功应用于人脸识别［14］、手写数字识别［15］、时间序列预测［16］及岭回归［17］等领域。

ELM算法存在结构选择的问题，即有效地确定网络隐含层结点的个数。确定ELM网络结构的算法可分为增量算法和剪枝算法2类。文献［18］提出了一种增量学习算法，该算法在初始化的单隐含层前馈神经网络基础上逐个或者逐组增加隐含层结点，直到算法的精度达到预定的目标。文献［19］提出了一种基于统计方法的剪枝算法，算法的基本思想是先初始化大量的隐含层结点，然后使用统计的方法对隐含层结点按重要程度进行排序，并剪掉重要程度低的隐含层结点。但该方法需要离散化预处理，容易产生信息丢失，且计算复杂度高。针对这一问题，本文提出了一种基于相容粗糙集技术的剪枝算法，用于确定ELM网络的结构。

1 基本概念

1.1 相容粗糙集

相容粗糙集理论［9］是经典粗糙集理论的推广，它用相容关系（或相似关系）代替不可分辨关系（或等价关系），不仅可以发现属性值之间的相似性，还可以消除属性值之间的微小偏差，从而提高系统决策的鲁棒性，也可有效提高决策的效率。在相容粗糙集理论中，按相容关系划分得到的相容类一般不构成对论域的划分，而是构成对论域的覆盖，即把知识看作是关于论域的覆盖。

定义1 信息系统是一个四元组IS＝（U，A，V，F）。其中，U＝｛x1，x2，…，xn｝为有限对象的非空集合，称为论域；A为用于描述对象的属性的集合为属性a∈A的取值范围；F∶U×A→V称为信息函数，满足∀a∈A，∀x∈U，F（x，a）∈Va。若A＝C∪D，C为条件属性集合，D为单决策属性，则称IS为决策系统或决策表，记为DT＝ （U，C∪D，V，F）。

定义2 给定决策系统DT＝（U，C∪D，V，F），R为定义在论域U上的二元关系，R为相容关系（或相似关系），当且仅当R满足：

（1）自反性。∀x∈U，有xRx。

（2）对称性。∀x，y∈U，若xRy，则yRx。

对 于 给 定 的 决 策 系 统DT＝（U，C∪D，V，F） ，可以在论域U上定义多种相似关系R［14］，即

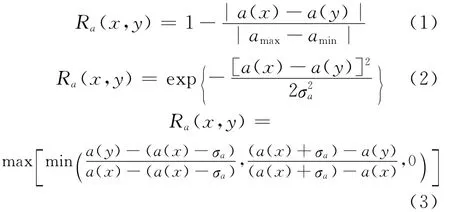
其中，a∈C；σa为属性a的方差；a（x）和a（y）分别为样例x和y在属性a上的取值；amax∈Va和amin∈Va分别为属性a的最大值和最小值，称Ra为由属性a诱导出的相似关系。对于∀P⊆C，定义属性子集P诱导出的相似关系RP［15－16］为：

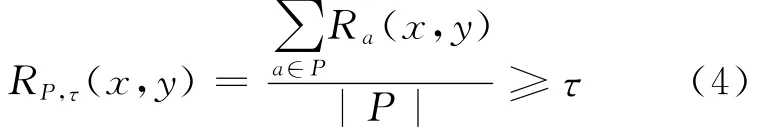
或

其中，τ∈［0，1］为相似性阈值。

定义3 给定决策系统DT＝（U，C∪D，V，F），P⊆C，RP为由属性子集P诱导出的相似关系。对于∀x∈U，定义x的RPτ相似类（或相容类为：

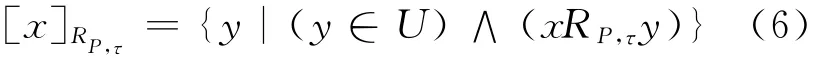
定义4 给定决策系统DT＝（U，C∪D，V，F），P⊆C，RP为由属性子集P诱导出的相似关系。U／D＝｛U1，U2，…，Uk｝是决策属性D对论域U的划分。定义Ui关于RP的τ上近似和τ下近似分别为：

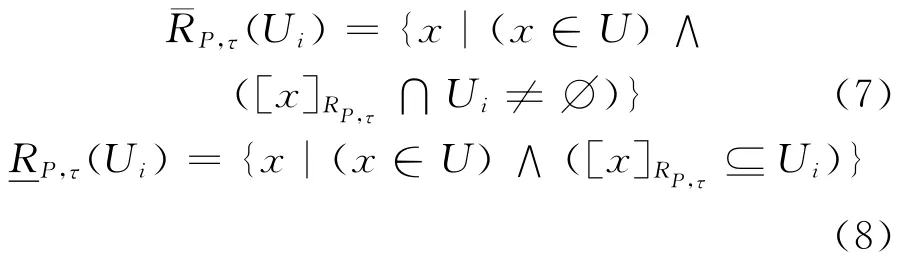
定义5 给定决策系统DT＝（U，C∪D，V，F），P⊆C，RP为由属性子集P诱 导出的相似关系，则称（9）式为P相对于D的τ正域，即

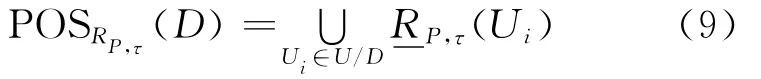
定义6 给定决策系统DT＝（U，C∪D，V，F），P⊆C，RP为由属性子集P诱 导出的相似关系，称（10）式为D相对于P的τ依赖度，即

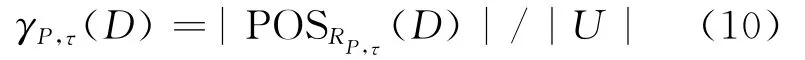
1.2 ELM 算 法

给定训练集D＝｛（xj，yj）｜xj∈Rn，yj∈RK｝，j＝1，2，…，M。ELM是用于训练如图1所示的单隐含层前馈神经网络的算法，网络的输入层结点个数为n，隐含层结点个数为N，输出层结点个数为m。输入层结点和输出层结点的激活函数均为线性函数，隐含层结点的激活函数为Sigmoid函数。wi＝（w1i，w2i，…，wni）是输入层的n个结点连接到隐含层第i个结点的连接权，i＝1，2，…，N。βi＝（βi1，βi2，…，βiK）是隐含层的第i个结点连接到输出层K个 结点的连接权，i＝1，2，…，N。该神经网络的模型为：

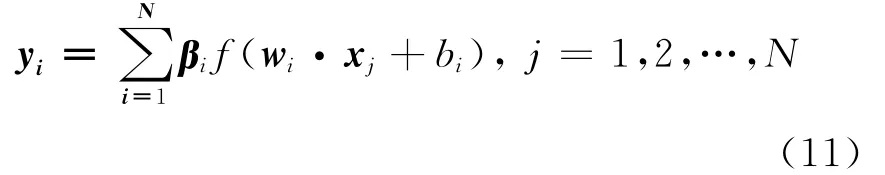
（11）式的矩阵表示为：

其中，

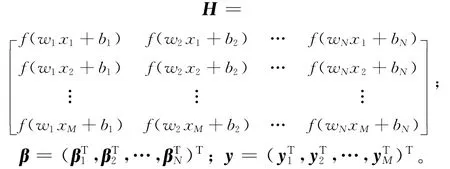
H称为隐含层输出矩阵，H的第i列是第i个隐含层结点关于输入样例x1，x2，…，xM的输出。H可逆时，权值β可以通过β＝H－1y求得，然而在大多情况下，训练样例个数远远大于隐含层结点数量；矩阵H不可逆，上述方法便行不通。ELM算法使用Moore－Penrose广义逆来近似求解权值β，即＝H＋y，其中H＋为隐层输出矩阵H的 Moore－Penrose广义逆矩阵。ELM 算法描述为：

（1）随机初始化输入层到隐含层的权值wi和偏置bi，i＝1，2，…，N。

（2）计算隐含层输出矩阵H。

（3）计算隐含层到输出层的权值＾β＝H＋y。

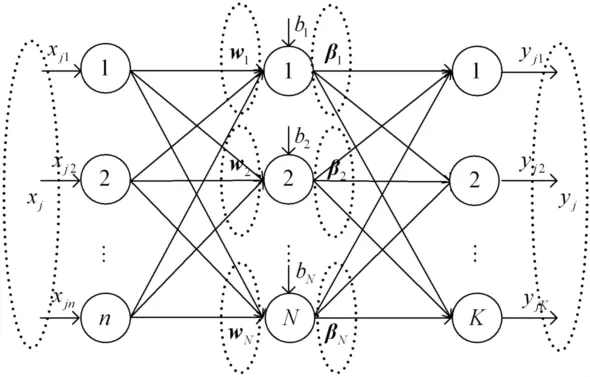
图1 单隐含层前馈神经网络

2 基于相容粗糙集的ELM网络结构选择

在ELM算法中，输入层到隐含层实际上是一个随机映射，它把n维样例空间映射到了一个N维特征空间。隐含层输出矩阵H的行对应映射后的样例点，列对应特征空间的维数（属性）。实际上，H为原样例集合经随机映射后，在N维特征空间中对应的样例集合。为描述方便，设H的第i列用ai表示（i＝1，2，…，N）。因为不同列对应不同的隐含层结点，所以决策属性D对ai的依赖度可用来表示隐含层结点i的重要度（i＝1，2，…，N），即对分类的贡献。本文可以将对分类没有贡献或贡献非常小的隐含层结点剪掉，算法首先将数据集分为训练集Tr和验证集Tv，然后从一个初始化的具有较多隐含层结点的SLFN开始，每次剪掉一个隐含层结点，直到满足预定义的终止条件为止。算法的终止条件是使C（p）达到其最小值，C（p）定义为：

其中，RSS（p）＝－yi）2；ti为 SLFN 的实际输出；Nv为验证集Tv中所含样例的个数；σ2为SLFN在训练集Tr上的均方误差的标准差；p为当前网络隐含层结点的个数。算法描述为：

（1）令τ＝τ0，将数据集划分为交集为空集的2个子集Tr和Tv。

（2）初始化SLFN为含有M个隐含层结点的网络，并用ELM在Tr上训练该网络。

（3）对隐含层权矩阵H的每一列ai，即对隐含层每一个结点i，用 （ 10）式计算γai，τ（D）。

（4）令ak＝

（5）剪掉ak所对应的隐含层结点k，得到新的网络SLFN，并在Tr上重新训练新的网络SLFN。

3 实验结果

为了进一步验证本文算法的有效性，本文在8个UCI数据库［20］上进行了实验，实验所用数据库的基本信息见表1所列。实验环境是PC机，双核1.86GCPU，2G内存，Windows XP操作系统，Matlab 7.1实验平台。实验采用十折交叉验 证 的 方 法，与 原 始 ELM 算 法［12］、BP 算法［21］、文献［18］和文献［19］中的方法进行了比较。实验中相容依赖度参数τ取为0.90，实验结果见表2所列。从表2可以看出，本文提出的方法在训练时间和测试精度上均优于其他方法。

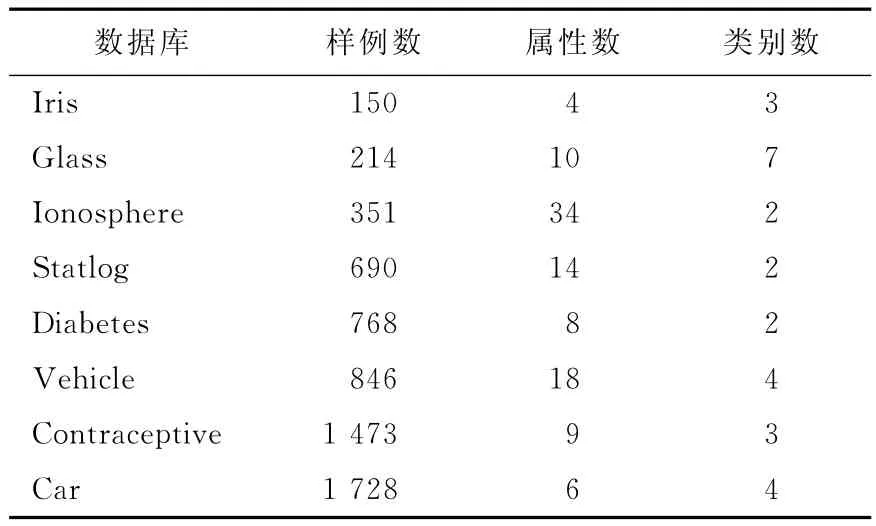
表1 实验所用数据库的基本信息

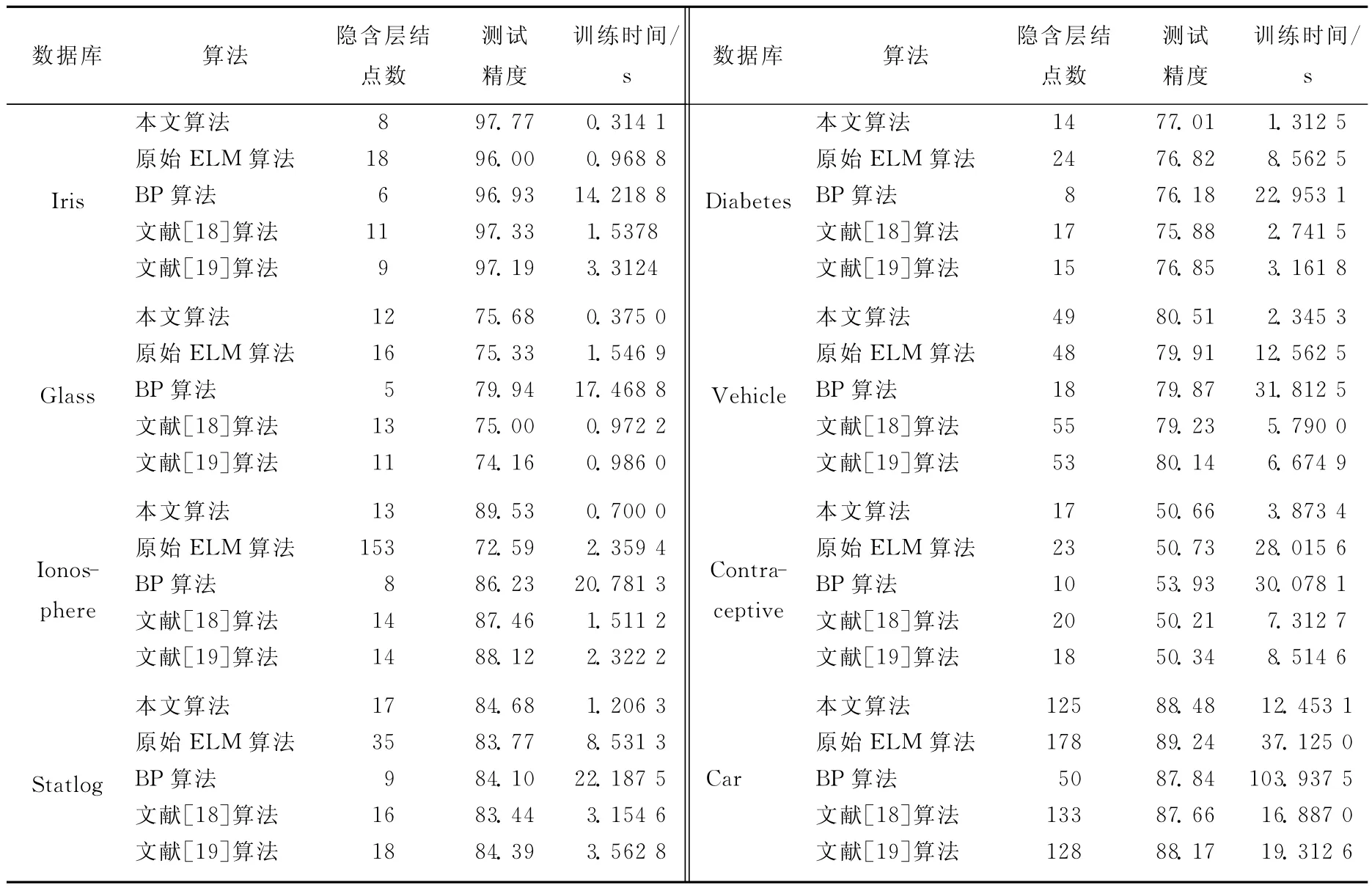
表2 与相关方法进行比较的实验结果

4 结束语

针对文献［18］中提出的剪枝算法需要离散化预处理，有信息丢失、计算复杂度高等问题，本文提出了基于相容粗糙集技术的ELM网络结构选择算法，该算法用相容依赖度来度量ELM网络中隐含层结点的重要性，递归地剪掉对分类没有贡献或贡献不大的隐含层结点，直到满足预定义的终止条件。实验结果表明，本文算法是行之有效的。

［1］ Pawlak Z.Rough sets［J］.International Journal of Information and Computer Sciences，1982，11：341－356.

［2］ 苗夺谦，李道国.粗糙集理论、算法与应用［M］.北京：清华大学出版社，2008：34－66.

［3］ Ziarko W.Variable precision rough set model［J］.Journal of Computer and System Sciences，1993，46（1）：39－59.

［4］ Yao Y Y.Probabilistic rough set approximations［J］.International Journal of Approximate Reasoning，2008，49（2）：255－271.

［5］ Yao Y Y.Probabilistic approachs to rough sets［J］.Expert Systems，2003，20（5）：287－297.

［6］ Yao Y Y，Wong S K M.A decision theoretic framework for approximating concepts［J］.International Journal of Manmachine Studies，1992，37（6）：793－809.

［7］ Yao Y Y.Generalized rough set models［C］／／Polkowski L，Skowron A.Rough Sets in Knowledge Discovery.Physica－Verlag Heidelberg，1998：286－318.

［8］ Greco S，Matarazzo B，Slowinski R.Rough Approximation of a preference relation by dominance relations［J］.European Journal of Operational Research，1999，117（1）：63－83.

［9］ Skowron A.Tolerance approximation spaces［J］.Fundamenta Informaticae，1996，27（2／3）：245－253.

［10］ Dubois D，Prade H.Rough fuzzy sets and fuzzy rough sets［J］.International Journal of General Systems，1990，17（1）：191－208.

［11］ 王国胤，姚一豫，于 洪.粗糙集理论与应用研究综述［J］.计算机学报，2009，32（7）：1229－1246.

［12］ Huang G B，Zhu Q Y，Siew C H.Extreme learning machine：theory and applications［J］.Neurocomputing，2006，70（1／2／3）：489－501.

［13］ Huang G B，Wang D H，Lan Y.Extreme learning machines：a survey［J］.International Journal of Machine Learning and Cybernetics，2011，2（2）：107－122.

［14］ Mohammed A A，Minhas R，Jonathan Q M，et al.Human face recognition based on multidimensional PCA and extreme learning machine［J］.Pattern Recognition，2011，44（10／11）：2588－2597.

［15］ Chacko B P，Krishnan V R V，Raju G，et al.Handwritten character recognition using wavelet energy and extreme learning machine ［J］.International Journal of Machine Learning and Cybernetics，2012，3（2）：149－161.

［16］ Dusan Sovilj，Antti Sorjamaa，Qi Yu，et al.OPELM and OPKNN in long－term prediction of time series using projected input data ［J］.Neurocomputing，2010，73（10／11／12）：1976－1986.

［17］ 王改堂，李 平，苏成利.ELM岭回归软测量建模方法［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2011，34（8）：1150－1154.

［18］ Feng G R，Huang G B，Lin Q P，et al.Error minimized extreme learning machine with growth of hidden nodes and incremental learning ［J］.IEEE Transactions on Neural Networks，2009，20（8）：1352－1357.

［19］ Rong H J，Ong Y S，Tan A H，et al.A fast pruned－extreme learning machine for classification problem［J］.Neurocomputing，2008，72（2）：359－366.

［20］ Blake C L，Merz C J.UCI Repository of machine learning databases［EB／OL］.［2011－03－01］.http：／／www.ics.uci.edu／～mlearn／MLRepository.html.

［21］ Kumar S.Neural networks［M］.Beijing：Tsinghua Univesity Press，2006：167－176.