基于Pareto聚类免疫进化算法的发动机悬置系统优化与稳健性分析

张代胜， 张 旭， 李彦保， 贾 坤， 李友真

（1.合肥工业大学 机 械与汽车工程学院，安徽 合 肥 230009；2.合肥工业大学 交 通运输工程学院，安徽 合 肥 230009）

引发汽车振动和噪声的一个最主要振源就是发动机不平衡惯性力和转矩波动。发动机悬置系统除支撑发动机和变速器等部件外，还隔离发动机振动向车架的传递，并减轻路面与轮胎对车身激振所引发的动力总成振动［1］。因此，悬置系统设计的优劣直接关系到发动机振动向车体的传递，影响整车的NVH性能。发动机悬置系统的优化设计旨在合理选择悬置参数，保证由于各种可控和不可控因素的影响发生微小变差时，都能保证悬置系统的稳健性［2－3］。

本文将稳健设计思想应用于发动机悬置系统的解耦优化设计中，基于悬置系统振动解耦的能量分布建立优化目标函数，综合运用遗传算法、免疫进化算法、Pareto算法和聚类算法对悬置系统进行优化，同时利用Monte Carlo方法进行稳健分析。

1 发动机悬置系统数学模型

发动机和变速器的固有频率远大于悬置系统频率，因此可把发动机看作是空间弹性支撑的刚体。将悬置橡胶简化成三向刚度和阻尼系统，假定橡胶件的弹性是线性的，并可忽略不计其阻尼，则悬置系统可简化成质量刚度和阻尼模型，建立6自由度动力总成4点悬置模型［4］。

O－xyz为发动机动力总成质心坐标系，O为动力总成质心，x轴平行于发动机曲轴轴线指向发动机前端，z轴通过发动机总成质心竖直向上，由右手定则得出y轴。悬置点1、2、3、4平置于发动机的两侧，1、2为前悬置，3、4为后悬置。各悬置的刚度方向u、v、s与动力总成质心坐标x、y、z方向在同一条直线上。

取沿x、y、z轴的位移和绕x、y、z轴的转角为广义坐标，由拉格朗日方程可以得到悬置系统的振动方程为：

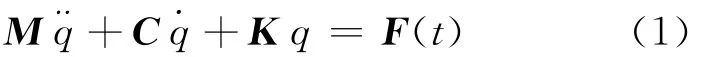
其中，M为系统的质量矩阵；C为系统的阻尼矩阵；K为系统的刚度矩阵；q为广义坐标。简化系统微分方程，即

质量矩阵为：

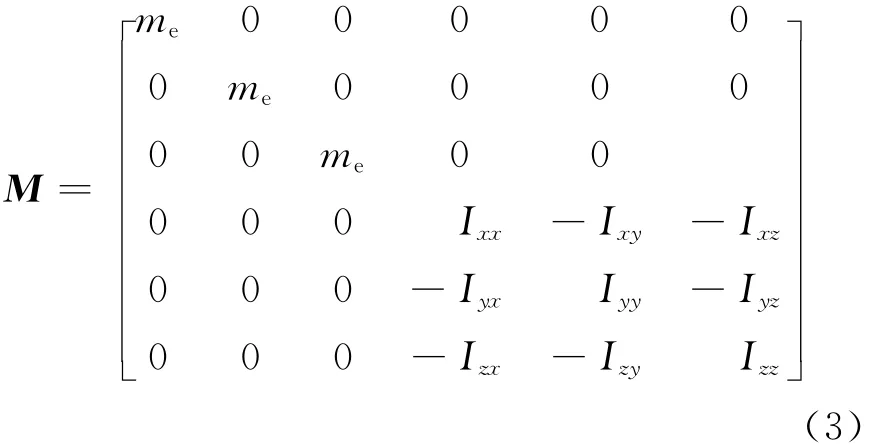
其中，me为动力总成质量；Ixx、Iyy、Izz和Ixy、Ixz、Iyz分别为转动惯量和惯性积。

刚度矩阵为：

其中，n为悬置点数目；Di为悬置垫三向主刚度矩阵，即

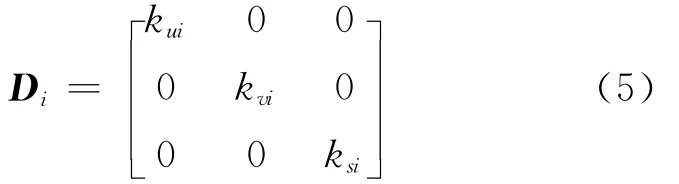
其中，kui、kvi、ksi分别为第i悬置点处悬置橡胶沿u、v、s主轴的刚度值。

Fi为物理坐标与广义坐标的变换矩阵，即

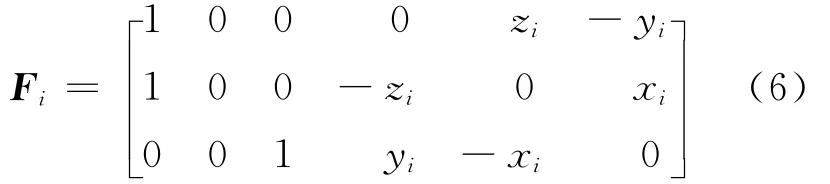
其中，xi、yi、zi分别为第i个悬置点的坐标。

Ci为方向余弦矩阵，即

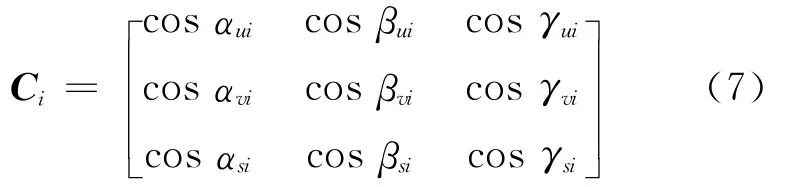
其中，αui、βui、γui为第i个悬置点处弹性主轴u正方向与x、y、z轴正向的夹角；αvi、βvi、γvi为第i个悬置点处弹性主轴v正方向与x、y、z轴正向的夹角；αsi、βsi、γsi为第i个悬置点处弹性主轴s正方向与x、y、z轴正向的夹角。

由（2）式可得动力总成悬置系统的固有频率ωj（j＝1，2，3，4，5，6）和固有振型φ。

2 能量解耦法

能量解耦法是从能量角度实现各自由度的解耦［5］，当系统以第j阶模态振动时，定义能量分布矩阵的第k行l列元素为：

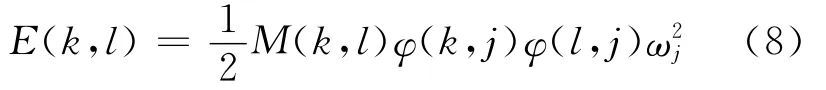
其中，k，l，j＝1，2，3，4，5，6；φ（k，j）、φ（l，j）分 别为第j阶振型的第k个和第l个元素；M（k，l）为系统质量矩阵的第k行、第l列元素；ωj为第j阶固有频率。

当系统以第j阶模态振动时，第k个广义坐标分配能量占系统总能量为：

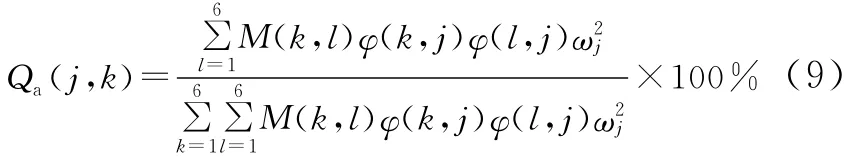
若Qa（j，k）＝100%，则系统做第j阶振动时，能量全部集中在k对应的广义坐标上，此时该模态振动完全解耦。

3 优化模型

3.1 基于Pareto聚类的免疫进化算法

考虑到在实际生产与使用过程中悬置垫参数都有很大的可变性，在悬置参数的优化设计中需要结合稳健设计的思想，既要保证最优解的高解耦率，又要保证最优解的可行稳健性。基于此，采用了Pareto聚类算法［6］。

对于极小化问题，Pareto解的定义为：对于可行解X＊，当且仅当不存在可行解X，使

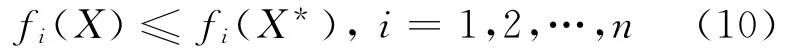
并且至少存在1个j∈ ｛1，2，…，n｝，使

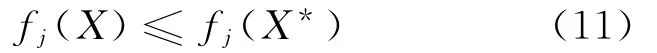
2个条件都满足时，可行解X＊为一个Pareto解［7］。Pareto聚类算法是综合Pareto算法与聚类算法［8］提出的一种复合算法。

定义1 对于一组数X＝ ｛x1，x2，…，xn｝，首先应用聚类算法把X分成m类（m≤n），得到m个子 种 群X1，X2，…，Xm，其 中Xi＝ ｛xi1，xi2，…｝；然后分别在每组中寻找个体∈Xi（i＝1，2，…，m），对任意xik∈Xi（i＝1，2，…，m）需满足f（）≤f（xik）或者f（）≥f（xik），则由组成的一组数｝称为X的Pareto聚类解。

根据IGA得出一组优化解，然后应用Pareto聚类算法求出全局最优解，完成一次迭代，算法流程如图1所示。遗传算法的编码方式采用所有变量的二进制编码串起来，组成20×n的二进制串，变异操作时分为3类，变异概率分别为0.03、0.1、0.5，记忆种群中解的个数为10，进化代数为50，采用基于欧几里得距离的方法聚类分析。

图1 发动机悬置系统稳健优化算法流程图

3.2 设计变量

影响发动机悬置系统特性的参数很多，例如悬置的安装位置、安装角度以及悬置橡胶的主刚度值等［4］。综合车架和动力总成设计限制，本文以悬置点处悬置橡胶的各向主刚度值K＝（k1，k2，…，kn）（n为悬置刚度个数）为设计变量，本文4个悬置点悬置刚度左右一致，共6个变量。

3.3 约束条件

（1）刚度约束。一方面为了限制发动机位置移动，要求悬置系统刚度不能太小；另一方面为了使系统具有较好的隔振性能，要求悬置系统刚度不能太大，即Kimin≤K≤Kimax（i＝1，2，…，n）。

（2）频率约束。悬置系统的最大固有频率必须小于发动机自身激励频率f的1／，才能起到隔振效果；为了避开路面激励频率，悬置系统最小频率应大于5Hz，即5≤ωj≤f／（j＝1，2，…，6）。另外，各阶频率之间间隔应大于0.5Hz。

3.4 目标函数

以实现悬置系统6自由度能量解耦最大为目标进行优化设计，把多目标优化转化成单目标优化。优化函数为：

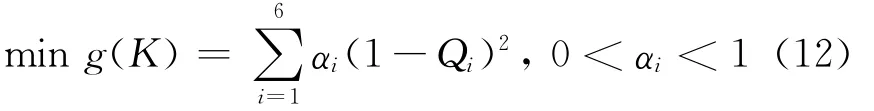
其中，Qi为各自由度上能量百分比；αi为加权因子。

3.5 优化实例

针对某款客车，发动机为6缸4冲程，4点悬置、平置式、对称分布。客车动力总成参数见表1所列，各悬置点主刚度值见表2所列。

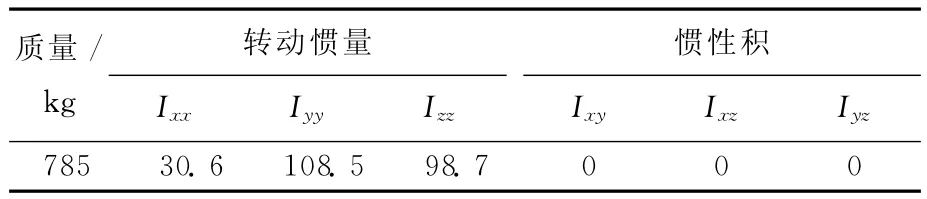
表1 动力总成系统参数 kg·m2

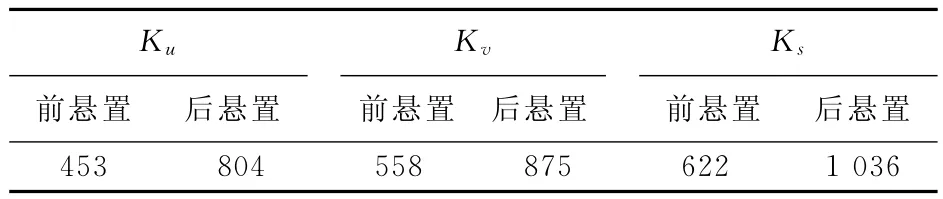
表2 各悬置点主刚度值 kg／m

由以上数据可计算出该悬置系统的6个固有频率和各频率下的能量矩阵，见表3所列。

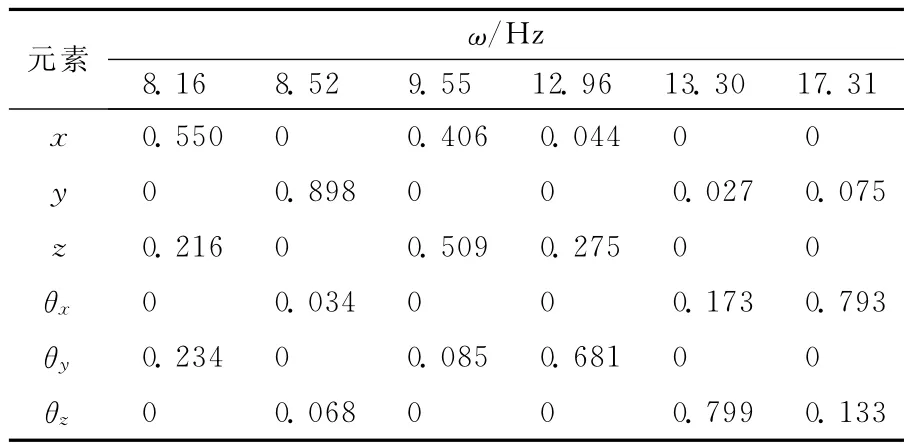
表3 优化前悬置系统固有频率和能量分布

根据表3数据，可以看到悬置系统固有频率满足频率约束条件为5≤ωj≤f／（j＝1，2，…，6），但是一阶与二阶固有频率间隔小于0.5。从能量分布上看，除横向y自由度外，其余各自由度方向能量分布小于80%，各自由度之间存在严重的振动耦合。

采用基于Pareto聚类的免疫进化算法，对以上悬置系统在Matlab环境下进行稳健性优化设计，从最终的记忆种群中提取3个最优解，结果见表4所列。

计算各优化解的固有频率和振动能量分布，见表5所列。

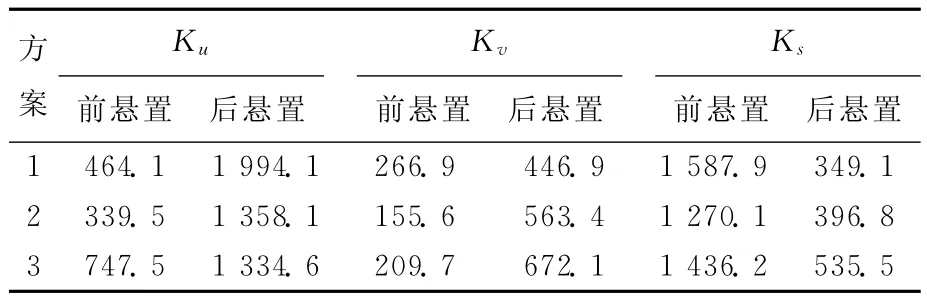
表4 优化后各悬置点主刚度值 kg／m

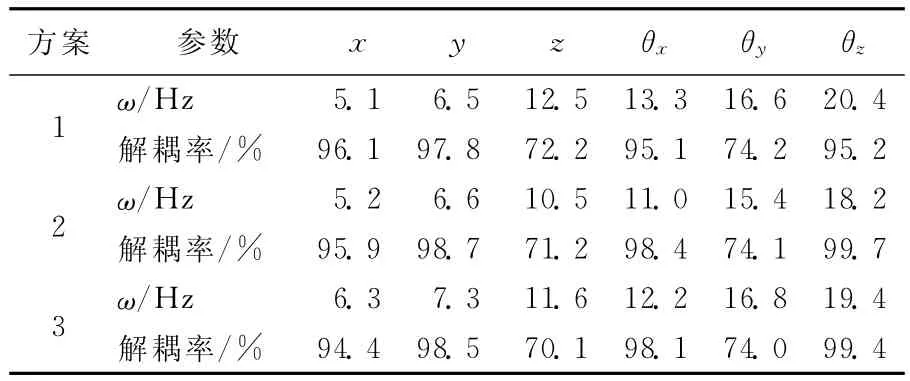
表5 优化后悬置系统固有频率和解耦率

由表5可知，3个优化解的频率都在合理的频率约束的范围内，且间隔都大于0.5。各自由度上的能量分布，除了z垂向与俯仰角θy方向分布较低外，其余自由度能量分布均大于95%。与原系统相比，在6个自由度上的振动能量分布均有显著提高，且平均提高18.3%。对于z垂向与俯仰角自由度，还可以通过改变悬置系统各悬置点的位置以及悬置安装角大小进一步优化。

4 基于Monte Carlo的稳健分析

在一系列生产与使用一段时间后的悬置垫样品中随机抽样检测发现，各向悬置主刚度基本上在±12%范围内波动，且分布曲线成正态分布。

Monte Carlo实质是通过随机变量的统计实验、随机模拟，求解数学、物理、工程技术问题近似解的数值方法［9］。建立优化目标函数的响应面模型，以各向主刚度为服从正态分布相互独立的随机变量。优化前的悬置刚度变量分布为：U1～N（453，54.362），U2～N（804，96.482），V1～N（558，99.962），V2～N（875，105.002），S1～N（622，74.642），S2～N（1036，124.322）。

对原系统进行稳健性分析，经过2 000次随机实验分析，通过计算可以得出响应面模型的概率分布为P1～N（2.485 9，0.806 12），目标函数的标准差为32.43%。优化前悬置系统目标函数的响应面模型概率分布和响应面拟合正态曲线，如图3所示。

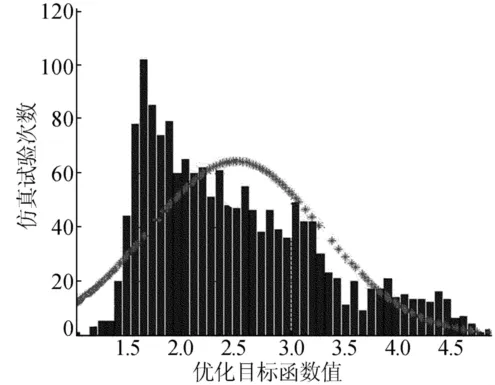
图2 优化前悬置系统响应面拟合正态曲线

根据设计要求，设计变量出现随机变化时，其产品性能变化最好不超过5%，此响应面的变化明显超出了允许值，稳健性较差。

对3个优化方案应用Monte Carlo算法进行稳健性分析，经过2 000次随机实验分析，计算得出3个方案的响应面模型的概率分布为：Q1～N（0.856 1，0.023 82），Q2～N（0.905 9，0.031 12），Q3～N（0.971 5，0.044 32）。

响应面模型概率分布和响应面拟合正态曲线，分别如图3～图5所示。

综上可知，3个方案的响应面目标函数的标准差分别为2.78%、3.43%、4.56%，均小于允许值。对比发现，优化后3个方案的稳健性均提高了几倍到十几倍。

采用Monte Carlo方法，分别对方案1的6个自由度上的解耦率建立响应面模型进行分析，其目标函数是基于单自由度解耦率建立的，消除彼此的影响，其响应面模型概率分布如图6所示，其中横坐标为解耦率，纵坐标为仿真次数。计算可得各自由度解耦率所构成响应面模型标准差分别为 0.94%、0.60%、0.36%、3.13%、0.60%、3.17%，各自由度都有很高的稳健性。由此可以判定，方案1无论是从总体上还是从局部自由度上，都具有较高的稳健性。同样方法求得，方案2与方案3同样具有较高稳健性。

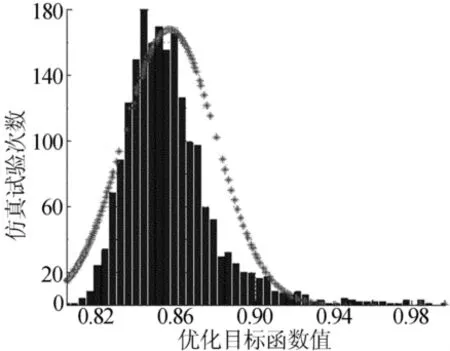
图3 方案1目标函数响应面拟合正态曲线

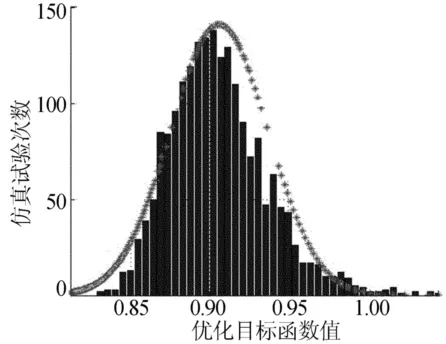
图4 方案2目标函数响应面拟合正态曲线

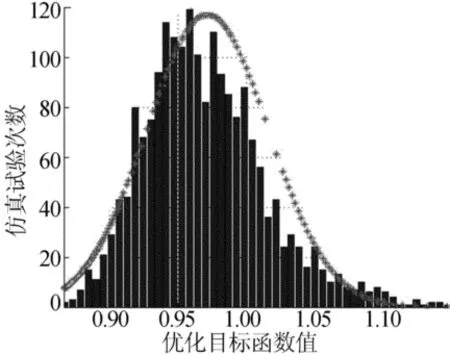
图5 方案3目标函数响应面拟合正态曲线

5 结束语

通过把Pareto算法、聚类算法、遗传算法、免疫算法相结合，对汽车动力总成悬置系统的解耦优化设计表明，基于Pareto聚类的遗传进化算法可以使发动机在怠速下达到比较满意的解耦程度。通过Monte Carlo验证优化解，还能保证悬置系统具有较高的稳健性，大大提高产品质量，在实际生产中有着较大的实际意义。

［1］ TamboliJ A，Joshi S G.Optimum design of a passive suspension system of a vehicle subjected to actual random road excitations［J］.Journal of Soundand Vibration，1999，219（2）：193－205.

［2］ Johnson S R，Subhedar J W.Computer optimization of engine mounting Systems［C］／／SAE Technical Paper 790974，1979.doi：10.4271／790974.

［3］ Sorge F.A simple model for the axial thrust in V－belt daves［J］.Journal of Mechanical Design，1996，l18：589－591.

［4］ 黄 信，柏世川，章竹一.汽车发动机悬置系统设计［J］.合肥工业大学学报：自然科学版，2009，32（Z1）：125－127.

［5］ 徐石安.汽车发动机弹性支承隔振的解耦方法［J］.汽车工程，1995，17（4）：198－204.

［6］ 王煦法，张显俊，曹先彬，等.一种基于免疫原理的遗传算法［J］.小型微型计算机系统，1999，20（2）：117－120.

［7］ 董 威.基于Pareto遗传算法的起重机主梁优化设计［D］.大连：大连理工大学，2005.

［8］ 梁志荣.数据挖掘中聚类分析的技术方法［J］.电脑开发与应用，2007，20（6）：37－40.

［9］ 张 蕾，董恩国，申焱华.基于蒙特卡罗法的气门弹簧稳健设计 研 究 ［J］. 机 械 科 学 与 技 术，2008，27（8）：1066－1069.