时域螺旋桨空泡噪声的球空泡脉动体积方法

况贶，张永坤

（1．海装上海局，上海200083;2．91439部队，辽宁大连 116041）

0 引言

空泡声学特性成为一个系统的研究课题有50多年的历史。单个球空泡的声学特性理论是比较完整的，而螺旋桨空泡噪声由于其复杂性，在很长时间里，对螺旋桨空泡噪声过多地依靠试验模拟。预报空泡噪声的理论工作，还是一个尚未完全解决的问题。

1 舰船螺旋桨空泡求解

螺旋桨空泡是一个十分复杂的问题，有些问题在机理上尚未完全解决，加之空泡范围和空泡形状也难以用试验方法准确验证，这都给空泡预报带来相应的困难。螺旋桨三维空泡问题有2种求解方法，一种是Kinnas和Lee［1－2］等采用的整体迭代求解方法;一种是Kim和熊鹰［3－4］采用的条带迭代求解方法。Kinnas和Lee采用整体迭代方法求解螺旋桨空泡形状和范围时，每次迭代求解的对象是整个螺旋桨。假定各半径处的空泡长度，将给定的空泡数直接代入Dirichlet型动力学边界条件，求出空泡的厚度分布。对于给定的空泡数，假定的空泡长度不能满足空泡末端厚度为0的条件，因此需要构造1个M维（M为桨叶展向的面元数）的Newton-Raphson迭代方程，通过迭代计算使所有展向位置空泡末端的厚度同时等于0，得到完全意义下的空泡范围。熊鹰［4－6］采用条带迭代方法求解螺旋桨空泡时，依次对螺旋桨各弦向条带进行求解，且对某一弦向条带求解时，其他弦向条带的影响认为是已知的。各条带之间的干扰通过迭代过程来考虑，即桨叶上的空泡是在沿弦向分布的条带上进行局部调整确定的。当设定空泡长度时，选取空泡厚度的初始值（一般设为0，空泡表面和桨叶表面重合），将控制方程应用于N个控制点上可得到N个线性方程，此时引入了1个新的未知数:空泡起始点的速度，故需从空泡末端封闭条件导出1个补充方程，联立求解后得到各未知奇点强度和空泡起始点处速度，由运动学条件可确定新的空泡形状，再将面元重新布置在求得的空泡表面上，进行迭代计算，直到求得的空泡厚度收敛为止。

对于单气泡空化噪声，一般只考虑体积脉动的影响，声压用体积的加速度来表示。

其中，C为液体中的声速;r为观测点到空泡初始中心的距离;ρ为液体密度。体积的加速度用泡半径的变化规律给出如此已知空泡的溃灭过程就可以得到空泡溃灭的发声情况。计算结果表明，在空泡的初生阶段与溃灭后期辐射的声压较高，而在中间阶段辐射的声压较低。

2 螺旋桨空泡噪声时域解法

2.1 单空泡辐射噪声特性

Lighthill从质量守恒和动量守恒方程出发得到声发生的普遍微分方程，出现了流体动力声源及其他辐射声场系统、全面的理论分析，因此Lighthill对流体动力声源的分析是十分重要的。

空泡在液体中所辐射的声压满足广义的Lighthill方程［7］:

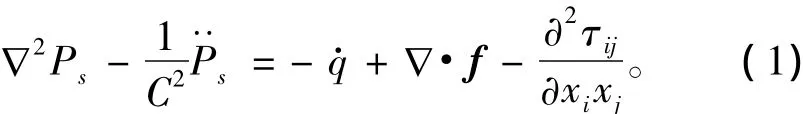
式中:Ps为声压;C为声在水中传播速度;q为单位体积内的质量脉动速率;f为脉动外力;τij为流体应力张量。式（1）右边的3个源项分别代表了3种主要类型的辐射源。第1项代表进入到流体中的非平稳质量流，它的作用与1个单极子相当;第2项是施加在某些界面上的非定常力的散度，具有偶极子的性质;第3项代表流体本身的湍流应力，具有四极子性质。这3种声源的辐射效率为

其中，m为声源的阶数（单极子m=1、偶极子m=2、四极子m=4）;k为波数，a为声源的特征尺寸。

对于空泡而言，由于实际情况中的空泡非常小，故ka＜＜1。因此由上式可知:极子阶数越小，辐射效率越高。单极子存在时，单极子对声辐射起主导作用。假定单空泡辐射的声压仅与质量脉动单极子声源有关，式（1）可简化为:

式中:ρ为液体密度;t'=t－r/C为延迟时间;r为观测点距泡中心的距离;V为任意时刻空泡体积。

假定液体密度的起伏忽略不计，式（3）也可表示为:

式（4）是小脉动单极子声源辐射的一般表达式，这种声源的强度正比于空泡体积变化加速度与液体密度的乘积。

2.2 面元法计算螺旋桨空泡体积变化

如果空泡形状已知，则可由空泡形状预报空泡体积变化。各个对应时刻的空泡形状求2次导数即可求得空泡体积变化，再通过Lighthill方程预报声压。此部分介绍计算螺旋桨空泡噪声的面元法。首先给出螺旋桨空泡所满足的控制方程和边界条件，通过这些方程迭代求解出螺旋桨空泡形状变化。

2.2.1 螺旋桨空泡控制方程

螺旋桨扰动速度势的积分方程为［9］:

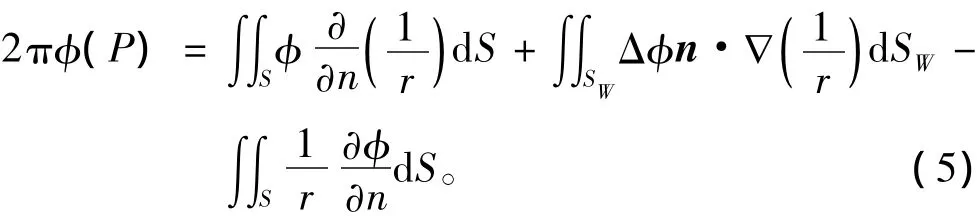
式中:φ（P）为桨叶表面上任一点P的扰动速度势，相当于P点分布的偶极子强度μ;Δφ=φU－φL，相当于尾流面上分布的偶极子强度μW;令σ=∂φ/∂n，相当于分布在桨叶表面的源强。

2.2.2 螺旋桨空泡边界条件

1）运动学条件

在桨叶表面上任一点的扰动速度和该点的来流速度在法线方向上相等。式中:n为S的外法线;VI为相对来流速度，对于螺旋桨而言，VI=Vs+Ω×r。由于右端项已知，上式表示了1个Neumann边界条件。

2）无穷远条件

3）Kutta条件

在初步的计算中采用Morino引入的1种近似的Kutta条件，即

扰动速度势在无穷远处满足

螺旋桨桨叶上的流动和二维流动存在很大差别，在计算的过程中采用压力相等的Kutta条件:

4）空泡区域的动力学条件

从物理上讲，空泡区域的动力学条件即是要求空泡内部及空泡表面上的压力保持为水的汽化压力Pv不变。在定常流中，可根据Bernouli方程将动力学条件以空泡上的合速度为常数的形式表示为:

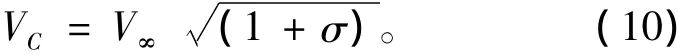
式中:σ为以无穷远来流速度V∞定义的空泡数。Kinnas［10］给出了三维流动中的空泡动力学条件，他利用非定常Bernouli方程，并将空泡上的合速度以扰动速度势沿空泡表面的方向导数和来流速度分量表示（其中采用了在空泡表面合速度的法向分量为0的条件），然后将2个式综合起来得到以表示的空泡动力学条件，其中s是空泡表面沿流动方向的坐标。一般再对其进行积分，得到以扰动速度势φ表示的Dirichlet型动力学条件。通常以此条件确定空泡面元上的偶极子强度，但在计算过程中空泡面元一般并不是布置在真正的空泡表面上，以便减少迭代次数和计算量。为解决此问题，可以采用Kim［11］推导的Dirichlet型动力学条件，在依动力学条件确定空泡上的偶强时，其中的积分是沿着迭代出的空泡表面进行。

5）尾流面上条件

对于无空泡或局部空泡在桨叶上封闭的情况，尾流面上的运动学条件为:

即尾流面上法向速度不连续（不存在源汇）。而动力学条件为:

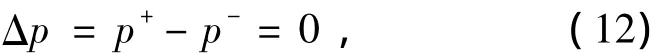
即尾流面上压力连续。对于超空泡的情况，尾流面上存在表示空泡的源汇

在非定常流中，求解局部空泡时仍与无空泡时一样，假设尾流面与时间无关;而求解超空泡问题时则与时间有关。尾流中的空泡形状可根据空泡表面方程对时间的导数为0的条件确定，如Kinnas在文献［10］中假定沿展向的横向流动速度是小量，得出确定尾流中超空泡形状的偏微分方程，

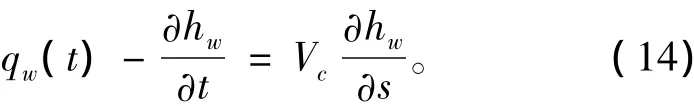
式中:hw为空泡厚度;Vc为空泡表面流动的总速度; s为空泡表面沿流动方向的坐标。

6）空泡末端封闭条件

在三维空泡流求解中，通常采用封闭的空泡末端模型，即要求空泡尾缘处空泡厚度为0，即

式中:Scte为局部空泡尾缘的弦向位置。

根据式（5）～式（15）编写了螺旋桨空泡形状计算公式。应用此程序对模型空泡情况进行计算，并做了一定的修正。

2.3 桨模网格划分以及噪声计算

时域噪声计算对象为模型桨，桨模按照一定的缩尺比与实船对应起来。采用Matlab绘制桨模网格划分图，如图1所示。螺旋桨桨叶数为5，径向单元数与弦向单元数分别为100和150，桨毂周向单元为50，网格划分均采用余弦划分。单元数的多少影响计算速度及计算精度，通过数次计算认为，本文所选取单元数在精度上可达到要求。模型计算的其余参数通过相似定律计算得出。桨模计算如表1所示。根据模型桨的数据及模型试验对应工况表，采用第2.2节中介绍的面元法对模型桨空泡形状进行计算。

图1 桨模网格图Fig.1Gridding chart of propeller model

表1 模型试验工况Tab．1Experiment conditions of model

由于空泡范围和形状都需要求解，通常先假定空泡范围迭代求解。因此，空泡起始点的位置需要事先确定。因为这一问题涉及到叶切面导缘附近的粘性流动，故在势流理论中一般假定空泡起始于切面的导缘。为了使计算方法具有更广泛的适用范围，可以结合螺旋桨非定常压力分布的形态与空泡数的比较确定空泡起始点的位置，以适合于计算空泡初生于桨叶切面弦向中部的情况。

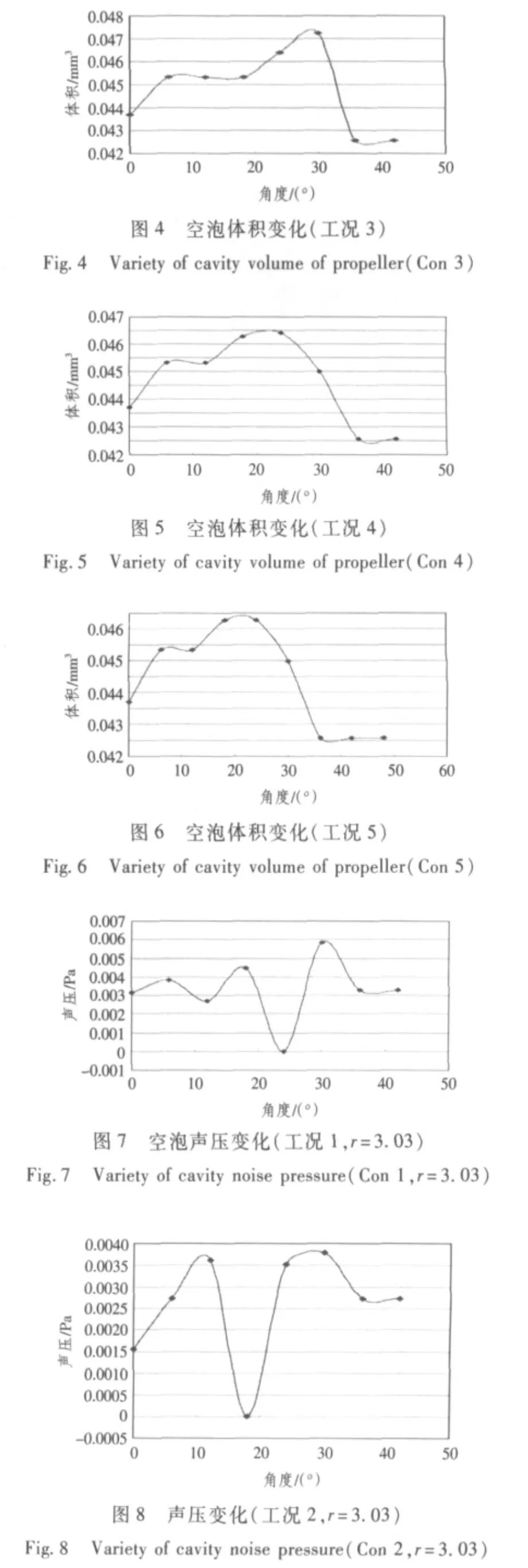
采用面元法计算出满足螺旋桨运动学条件以及空泡动力学的空泡体积的变化，然后通过单极子声理论，也就是式（4），计算出螺旋桨空泡噪声声压。此时计算出的螺旋桨空泡体积的变化是相对于角度变化的，在后续的内容中推导出随时间变化的空泡以及空泡噪声，计算结果如下图所示。图2～图6是5种工况下空泡体积随角度变化图;图7～图11为半径取3.03 m声压随角度变化图;图12～图16为半径取2.03 m时声压随角度变化图;图17和图18反映了不同航速、不同距离对噪声的影响规律。

3 时域空泡噪声计算方法

3.1 随时间变化声压与随角度变化声压关系

在第2节中时域螺旋桨空泡体积以及空泡噪声的数值是随螺旋桨角度变化的，根据此结果，在本节推导出随时间变化的螺旋桨空泡噪声。

水中声压计算公式如下［12］:

式中:pref=10－6Pa为参考声压。

压力随时间的变化p（t）与压力随角度变化p（θ）之间的关系为:

式中:ω为桨角速度，（°）/s;n为桨转速，1/s。对式（17）两边进行积分，可得:

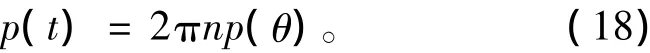
将式（18）代入式（16），可得随时间变化声压表达式:

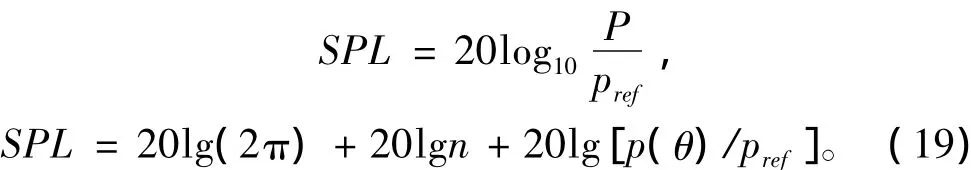
3.2 舰船螺旋桨空泡噪声计算方法

1）球空泡脉动体积方法

首先，应用面元法计算出满足螺旋桨工作条件以及空泡动力学条件的空泡形状，求解出空泡体积的变化规律;其次，根据Lighthill的理论，当单极子存在时，单极子对噪声的贡献远远大于其他极子，可以将螺旋桨整体作为一个球来处理，得到声压与空泡体积之间的关系。最后，将空泡体积的变化代入简化的Lighthill方程，求解出时域螺旋桨空泡噪声的变化规律。

2）单气泡理论计算螺旋桨空泡噪声

对于单气泡空泡噪声，考虑体积脉动的作用，声压用体积加速度来表示。

式中:C为液体中声速;r为观测点到空泡初始中心的距离;ρ为液体密度，体积加速度由泡半径的变化规律给出这样，已知空泡半径变化规律即可计算出空泡噪声。本文也称为半径变化方法。

3）FWH方程方法

使用面元法计算空泡体积变化，然后代入FWH方程，计算螺旋桨空泡噪声。

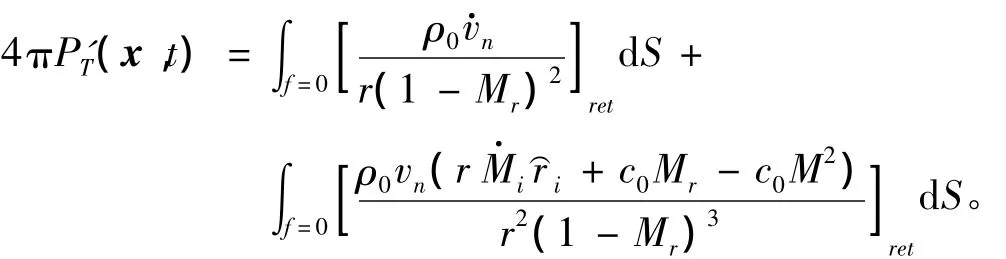
式中:P'T为由厚度导致的声压，对应于单极子;桨叶旋转、非定常片空泡体积振动作为单极子源，桨叶表面脉动压力作为偶极子源;M为马赫数;Mr为径向马赫数。

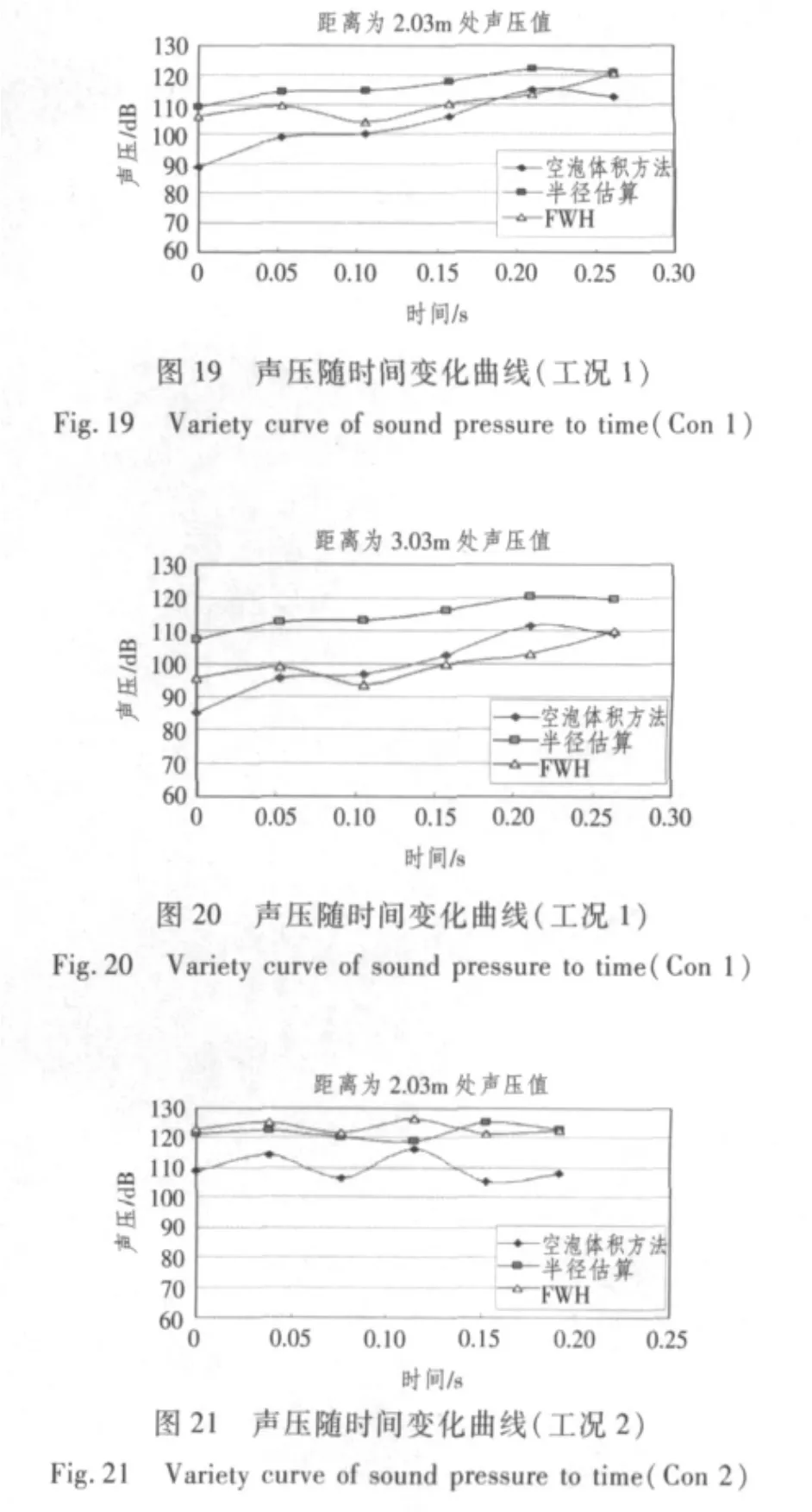
随时间变化的声压与随角度变化声压关系如式（18）所示。声压计算公式如式（19）所示。3种方法计算结果如图19～图28所示。

4 时域螺旋桨空泡噪声计算结果分析

图2～图6反映了5种工况下空泡体积随角度变化，从图中可以看到随着航速增加，空泡体积最大值有前移的趋势。

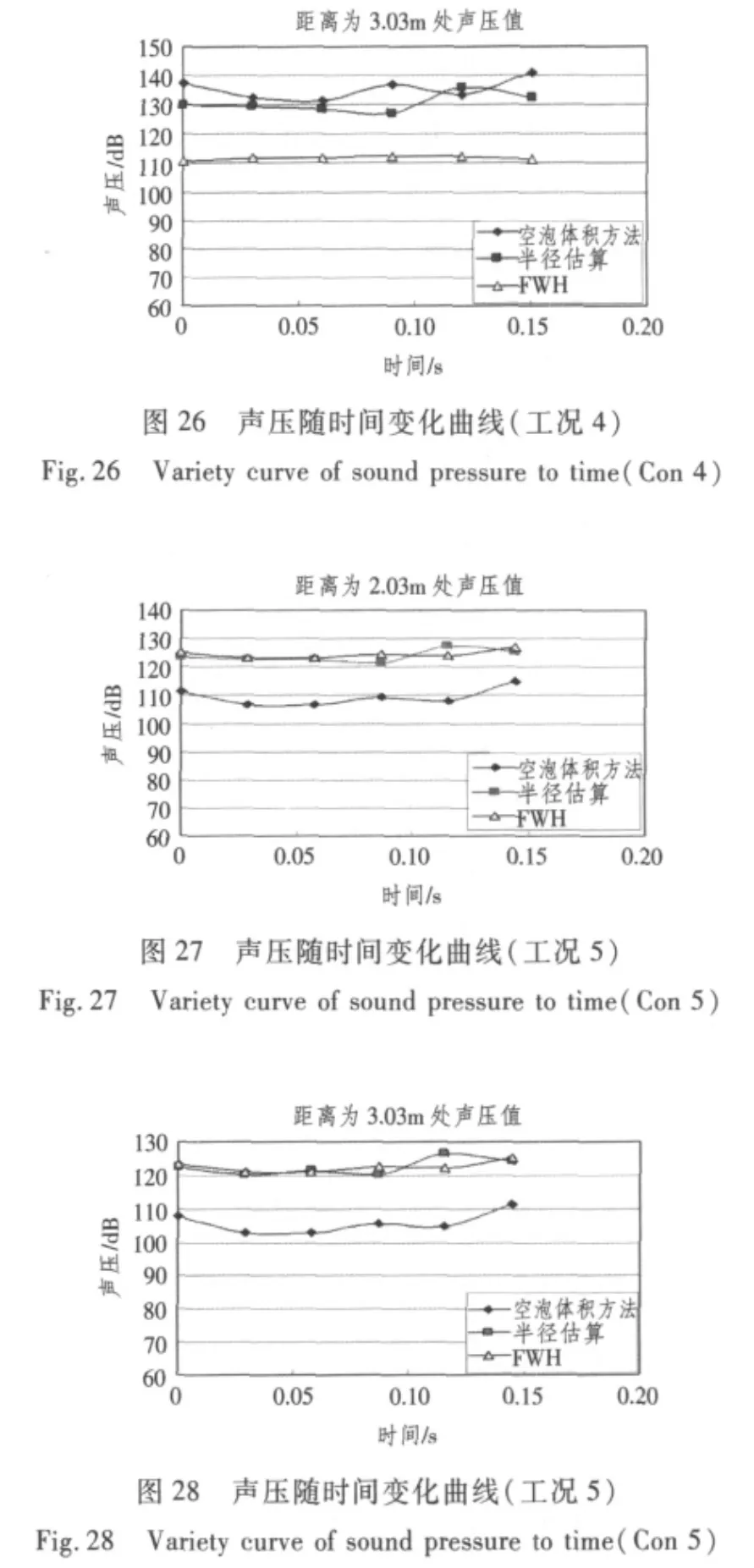
图7～图11为距离3.03 m处声压随角度变化值;图12～图16为距离2.03 m处声压随角度变化值。图17和图18为2种不同距离、不同航速下噪声谱。由图17和图18可以看出，螺旋桨空泡噪声有准周期性特点。对于螺旋桨空泡来讲，空泡是桨叶在船尾不均匀流场作旋转过程中不断产生不断破灭的。桨叶不断地交替经过空泡形成的低压区和高压区，在不均与流场和桨叶旋转共同作用下，无数空泡不断交替地产生和破灭，故具有准周期的特点。5种工况下准周期排列顺序为:T5＞T4＞T3＞T2＞T1。周期小，说明变化快。振幅的排列顺序为A3＞A1＞A2＞A4＞A5。

图19～图28反映了3种不同数值方法的计算结果。从3种算法自身的假定条件来讲，球空泡脉动体积方法考虑问题最全面，空泡满足水动力学边界条件以及空泡动力学条件。单气泡理论（半径收缩变化）只是对噪声的现象进行说明，对噪声的数值进行大概的估算，精确度不是很高。FWH方程计算螺旋桨空泡噪声时，没有考虑流场以及负荷情况，只是把空泡体积变化代入厚度噪声项进行了计算。这3种方法中球空泡体积方法计算结果最为可信。

5 结语

螺旋桨空泡噪声由于空泡的瞬时性、非线性给数值计算带来很大的难度。结合模型试验以及空泡形状的算法，本文将螺旋桨空泡噪声的计算分为频域及时域方法2类。频域采用回归方法进行计算，计算结果同模型试验的结果进行比较分析;时域方法分为2步进行求解。首先使用面元法计算出空泡体积变化规律，然后通过简化的Lighthill方程计算出螺旋桨空泡噪声。具体内容如下:

1）螺旋桨空泡噪声频域计算采用回归方法结合试验研究的方法进行。模型试验与实船航行状况相对应，分别对5种工况下的螺旋桨空泡噪声进行了测量。对应于这5种工况，分别采用了2种回归方法对桨模的空泡噪声进行了计算，计算的结果同模型试验的方法进行了比较，在20 kHz的范围以内，三者的吻合度很好，超过此范围，个别的测点存在一定的偏差。因此可以说在一定的频域范围内，三者的结果吻合较好。

2）对螺旋桨空泡噪声进行时域求解时，首先应用面元法计算出满足螺旋桨工作条件以及空泡动力学条件的空泡形状，求解出空泡体积的变化规律。其次根据Lighthill的理论，当单极子存在时，单极子对噪声的贡献远远大于其他极子，可以将螺旋桨整体作为一个球来处理，得到声压与空泡体积之间的关系。最后将空泡体积的变化代入简化的Lighthill方程，求解出时域螺旋桨空泡噪声的变化规律。

3）根据模型试验的工况，对5种航速下，2个测点的螺旋桨空泡噪声进行连续计算。验证了噪声随半径的衰减规律，求证了航速对噪声的影响。随着航速的增加，空泡存在周期变小，说明空泡变化剧烈。

4）3 种方法计算结果说明，空泡体积脉动球方法是可信的。单气泡理论可以对声压变化做大概估算，精确度不高;FWH方程方法在本文计算中做了很大的简化，准确度不高。应用FWH方程方法计算螺旋桨空泡噪声不但要计算流场分布，同时计算结果也很片面。有待进一步深入研究。

［1］FINE K S．A numerical nonlinear analysis of the flow aroundtwo-andthree-dimensionalpartiallycavitating hydrofoils［J］．Journal of Fluid Mechanics，1993，254（1）: 151－181．

［2］LEE C S，KIM Y G，LEE J T．A potential based panel method for the analysis of a two-dimensional super-or partially-cavitating hydrofoil［J］．Journal of Ship Research，1992，36（2）:168－181．

［3］KIM Y G，LEE C S．Prediction of unsteady performance of marine propellerswithcavitationusingsurfacepanel method［A］．Proceeding of 21stSymposium on Naval Hydrodynamics，Trondhein，Norway，1996．913－929．

［4］XIONG Ying，YE Jin-ming，WANG De-xun．Prediction of unsteady cavitation of propeller using surface panel method［J］．Journal of Hydrodynamics，2005，35（1）:43－49．

［5］叶金铭，熊鹰．螺旋桨非定常空泡数值预报中的几个问题［J］．武汉理工大学学报（交通科学与工程版），2006，32（6）:961－964．

Ye Jin-ming，XIONG Ying．Numerical and experimental research on pressure fluctuations induced by propeller cavitation［J］．Journal of Wuhan University of Technology （Transportation Science＆Engineering），2006，32（6）:961－964．

［6］叶金铭，熊鹰．螺旋桨空泡数值研究［J］．哈尔滨工程大学学报，2006，23（2）:172－175，183．

YEJin-ming，XIONGYing．Numericalanalysisof propeller cavitation［J］．Journal of Harbin Engineering University，2006，23（20:172－175，183．

［7］戚定满．空化噪声特性研究［D］．上海:上海交通大学，2002．72－98．

［8］柳康宁．船舶水下噪声原理［M］．上海:上海交通大学出版社，1982．223－245．

［9］叶金铭．推进器水动力性能及空泡预报的数值方法和模型试验研究［D］．武汉:海军工程大学，2008．

［10］FINE KS．A nonlinear boundary element method for the analysis of unsteady propeller sheet cavitation［A］．19thSymposium on Naval Hydrodynamics，Seoul，Korea，1992．102－112．

［11］KIM，Y G LEE C．Prediction of unsteady performance of marinepropellerswithcavitationusingsurface-panel method［A］．21stSymposium on Naval Hydrodynamics，TRondhein，Norday，1996．913－929．

［12］杜功焕，朱哲民，龚秀芬．声学基础［M］．南京:南京大学出版社，2006．193－195．