一类具偏差变元的p-Laplacian方程的周期解＊

唐美兰，刘心歌

（中南大学数学与统计学院，湖南长沙 410083）

一类具偏差变元的p-Laplacian方程的周期解＊

唐美兰，刘心歌†

（中南大学数学与统计学院，湖南长沙 410083）

应用Manásevich-Mawhin连续性定理，研究了具偏差变元的含有2个p－Laplacian算子的微分方程周期解的存在性，获得了周期解存在的新的充分性条件，并通过实例说明本文结论的有效性.

周期系统；p-Laplacian算子；周期解；存在性；Manásevich-Mawhin连续定理

近年来，Rayleigh方程、Liénard型方程、Duffing方程因其具有广泛的实际应用背景，很多学者对其周期解的存在性问题一直怀着强烈的兴趣，得到了很多结论［1－9］.但因p-Laplacian算子的非线性，目前对具偏差变元的p-Laplacian方程周期解的存在性研究并不多.本文将研究含多个p-Laplacian算子的偏差变元p-Laplacian微分方程周期解的存在性问题.

1 引 理

考虑下列含多个p-Laplacian算子且具偏差变元的微分方程：

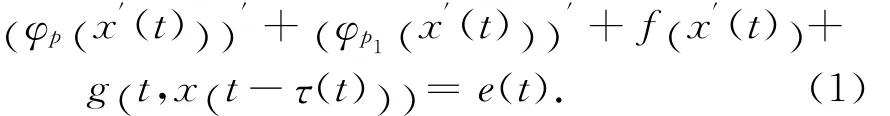
2π－周期解的存在性.其中f为定义在R上的实连续函数，p＞p1＞1，φp：R→R，φp（s）＝｜s｜p－2s，s≠0，φp（0）＝0，φp1：R→R，φp1（s）＝｜s｜p1－2s，s≠0，φp1（0）＝0，g是定义在R2上的连续函数，关于t是周期的且g（t，·）＝g（t＋2π，·），∀t∈R.e，τ是定义在R上的连续2π－周期函数.

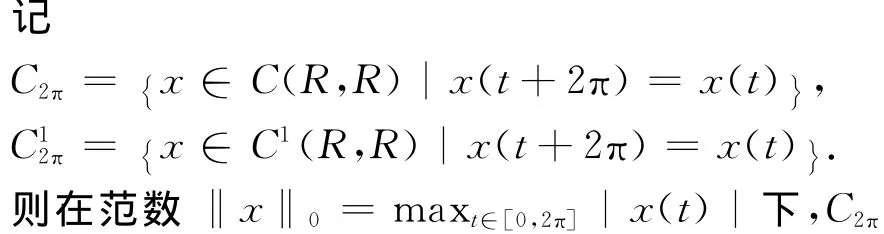
2 周期解的存在性

3 例子

例1 考虑下列方程：

4 结 论

本文应用Manásevich-Mawhin的连续性定理和一些分析技巧，在没有f（0）＝0和的条件下，得到了p-Laplacian方程（3）存在2π-周期解的新的充分性条件.

［1］ LIU Bing-wen.Periodic solutions for Liénard type p-Laplacian equation with a deviating argument［J］.Journal of Computational and Applied Mathematics，2008，214（1）：13－18.

［2］ LU Shi-ping.New results on the existence of periodic solutions to a p-Laplacian differential equation with a deviating argument［J］.Journal of Mathematical Analysis and Applications，2007，336（2）：1107－1123.

［3］ MÂNASEYICH R，MAWHIN J L.Periodic solutions for nonlinear systems with p-Laplacian-like operators［J］.Journal of Differential Equations，1998，145（2）：367－393.

［4］ ZHANG Fu-xing，LI Ya.Existence and uniqueness of periodicsolutions for a kind of Duffing type p-Laplacian equation［J］.Nonlinear Analysis：Real World Applications，2008，9（1）：985－989.

［5］ ZHOU Ying－gao，TANG Xian-hua.Periodic solutions for a kind of Rayleigh equation with a deviating argument［J］.Computers ＆Mathematics with Applications，2007，53（5）：825－830.

［6］ ZONG Ming－gang，LIANG Hong-zhen.Periodic solutions for Rayleigh type p-Laplacian equation with deviating arguments［J］.Applied Mathematics Letters，2007，20（1）：43－47.

［7］ XIAO Bing，LIU Bing-wen.Periodic solutions for Rayleigh type p-Laplacian equation with a deviating argument［J］.Nonlinear Analysis：Real World Applications，2009，10（1）：16－22.

［8］ WANG Gen-qiang，YAN Ju-rang.On existence of periodic solutions of the Rayleigh equation of retarded type［J］.The International Journal of Mathematics and Mathematical Sciences，2000，23（1）：65－68.

［9］ WANG Gen-qiang，CHENG Sui-sun.A priori bounds for periodic solutions of a delay Rayleigh equation［J］.Applied Mathematics Letters，1999，12（3）：41－44.

Periodic Solutions for a Kind of p-Laplacian Equation with a Deviating Argument

TANG Mei-lan，LIU Xin-ge†
（School of Mathematics and Statistics，Central South Univ，Changsha，Hunan 410083，China）

The existence of periodic solutions for a kind of p-Laplacian differential equation with two p－Laplacian operators was investigated.Based on Manásevich-Mawhin continuation theorem and some analysis skills，new sufficient conditions for the existence of periodic solutions were given.An example was provided to demonstrate the effectiveness of the proposed result.

periodic systems；p-Laplacian operators；periodic solutions；existence；Manásevich- Mawhin continuation theorem

O175.6

A

1674-2974（2012）08-0090-03＊

2011-07-10

国家自然科学基金资助项目（61070190）；中南大学前沿研究计划资助项目（2010QZZD015）；国家社会科学基金资助项目（10BJL020）

唐美兰（1972－），女，湖南邵东人，中南大学副教授，博士

†通讯联系人，E-mail：liuxgliuhua＠163.com