含有双曲函数非线性项的超混沌系统及其同步*
2012-03-19王春华尹晋文
余 飞,王春华,胡 燕,尹晋文
(湖南大学信息科学与工程学院,湖南长沙 410082)
由于超混沌系统具有两个或两个以上的正Lyapunov指数,相轨在更多方向上分离呈现更为复杂的动力学特性,使得超混沌系统在混沌保密通信和混沌信息加密等方面具有潜在的应用[1].目前,超混沌系统的产生与同步技术越来越受到研究者的关注而成为混沌研究的热点.自从R¨ossler[2]在1979年发现第1个超混沌系统以来,大量的超混沌系统相继提出,如王光义等[3]通过在3阶Lorenz系统中引入一个外加的状态变量构造了一个超混沌系统.刘扬正[4]在三维Lü系统的基础上增加一维状态构建了一个四维超混沌Lü系统.周平等[5]构造了只包含一个非线性项的四维超混沌系统.可以看出在所研究的众多新超混沌系统中,由于非线性项的不同导致了系统呈现出不同的超混沌特性,多数研究的非线性项均为系统的不同状态变量的乘积,对于含有双曲函数非线性项的系统是否会有同样的超混沌现象,其动力学行为特性目前尚未有研究.为此,本文在对这类自治系统研究的基础上,提出了一个新的四维超混沌系统,该系统非线性特征主要依赖于一个非线性二次双曲余弦项和一个非线性二次交叉项.
Pecora和Carroll[6]在1990年首次提出了混沌同步的原理,由于混沌同步在物理学、信息科学以及保密通信等领域存在重要的应用价值,几十年以来人们对其进行了广泛深入的研究,并且提出了用以实现混沌同步的多种方法,如主动和被动控制法[7-8]、线性和非线性反馈控制同步法[9-10]、基于观测器控制法[11]、滑模控制法[12]、自适应完全和反相同步方法[13]、Backstepping方法[14]、基于H∞控制器方法[15]和广义函数投影同步方法[16]等.最近,文献[5]提出了一种不删除驱动系统非线性信息的混沌同步方法,并利用严格数学理论证明了该混沌同步方法可行性,但是该方法只适用于2个同结构的超混沌同步,对异结构混沌同步会失效.本文通过对该方法的改进,实现了2个异结构的混沌同步,在同步过程中同样保留了驱动系统的非线性特性,而且通过调整控制参数,可控制同步收敛速度,使得驱动系统和响应系统能够快速精确达到同步.
1 新的超混沌系统及其基本动力学
超混沌系统的数学模型描述为:

式中:a,b,c,k∈R+;x,y,z,w为状态变量.与一般超混沌系统不同的是,系统(1)含有一个非线性二次双曲余弦项.当a=8,b=16,c=10,k=6,初始条件为[0.2,1,0.8,2]T时,系统轨迹的三维相图如图1所示.该四维超混沌系统的4个Lyapunov指数分别为l1=0.325 5,l2=0.121 6,l3=0,l4=-17.447 1,由此可以看出存在2个正的Lyapunov指数,表明该系统确实是超混沌系统.由图1可以看出,其吸引子结构与现有已发表的论文中所提出的四维超混沌吸引子结构完全不同,故本文提出的混沌或超混沌吸引子具有复杂的动力学行为.
由方程组(1)可得:


图1 超混沌吸引子相图Fig.1 Phase portraits of hyperchaotic attractors
这意味着,当t→∞时,包含系统轨线的每个体积元均以指数率-17收缩至零.因此,所有系统的轨迹最终渐近地运动到一个特定的零体积的极限集中,即固定在一个吸引子上.很明显,该混沌系统具有z轴对称性,即满足(x,y,z,w)→(-x,-y,z,-w)的不变性.
系统(1)的平衡点可以解下面代数方程求得:

很容易得出该系统有且仅有一个平衡点E(0,0,1/c,0),在该平衡点处对系统(1)进行线性化,对应的雅克比矩阵为:

特征方程为:

解得:

根据Routh-Hurwitz判据,有
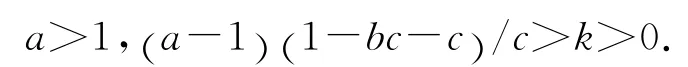
当满足上述条件时,系统(1)在平衡点E处是全局稳定的.图2为系统(1)的频谱,由图可知存在连续的宽频带特性.图3为在不同平面上所得到的Poin-care映射,可以看出Poincare映射图在一个固定区域内存在很多离散的、具有分层结构的点.

图2 log的频谱Fig.2 Spectrum map of log

图3 Poincare映射Fig.3 Poincare maps in planes where
2 超混沌系统(1)同步研究
将驱动系统和响应系统用下面形式表示:

式中:A,B分别为驱动和响应系统中的线性项系数矩阵,且A≠B为异结构同步;F1(X1),F2(X2)分别为驱动和响应系统的非线性项;U(X1,X2)为控制项,其表达式为:

式中:DF1(X1),DF2(X1)分别对应于F1(X1),F2(X1)的Jacobi矩阵;C为待定矩阵;e为驱动系统和响应系统的状态误差向量(假设驱动和响应系统的最高阶为n阶).

由式(4)~式(7)可得误差动力学系统方程为:

将所有响应系统的状态变量X2用驱动系统的状态变量X1和误差变量e表示,则式(8)的后2项将只剩下含有误差变量ei(i=1,…,n)的项.此时,ei=0(i=1,…,n)是误差系统(8)的平衡点,误差系统(8)在平衡点ei=0(i=1,…,n)处的Jacobi矩阵为A+C.如果矩阵A+C的所有特征值具有负实部,则驱动系统和响应系统可以达到同步.此外,改变矩阵C,可以调节同步收敛时间,从而获得最佳同步效果.
这里我们选取超混沌系统(1)为驱动系统,其数学模型重新描述为:

响应系统选取作者最近提出的一个具有完全四翼形式的四维混沌系统[17],其数学模型描述为:

式中:m,f,g,h,p∈R,当m=8,f=12,g=60,h=4和p=5时,系统吸引子具有完全四翼形式.
把驱动和响应系统写成向量形式,则驱动和响应系统的非线性项分别为:

可得:

计算F1(X1),F2(X1)的Jacobi矩阵DF1(X1),DF2(X1),分别为:

这里取待定矩阵
式中:k1,k2,k3,k4分别为控制系数,用来控制同步收敛的速度,需要选择合适的k1,k2,k3,k4使A+C的所有特征值具有负实部.
由式(6)可得如式(16)的控制器,将式(16)代入式(8)可得如式(17)的误差动力学方程.显然ei=0是误差动力学系统(17)的平衡点,误差系统在平衡点ei=0处的Jacobi矩阵为A+C.

此外,误差系统(17)中含有驱动系统的双曲余弦非线性项,从图4可以看出,其差值随时间变化趋向于零,故这一项并不影响误差系统在平衡点的Jacobi矩阵,只要满足k1<a,k2<-1,k3<c和k4<0.由于矩阵A+C的所有特征值具有负实部,所以平衡点ei=0是误差系统(17)的渐近稳定平衡点,故有成立,从而响应系统(10)和驱动系统
(9)可以达到全局渐进同步.
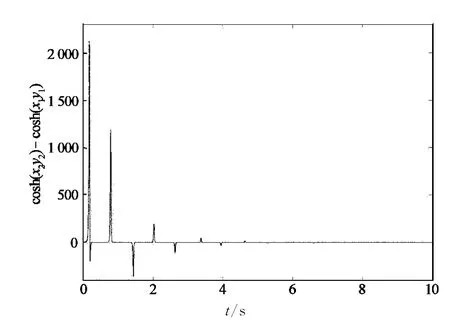
图4 驱动系统的非线性项差值随时间变化的曲线Fig.4 Curve of the difference of nonlinear term in the drive system with respect to time
为了验证该方法的有效性,采用4阶龙格-库塔法进行数值仿真,驱动系统的状态初始值为X1(0)=[0.2,1,0.8,2 ]T,系统参数为a=8,b=16,c=10,k=6;响应系统状态初始值为X2(0)=[2,1,1,2 ]T,系统参数为m=8,f=12,g=60,h=4,p=5,此时2个系统分别处于超混沌和混沌状态.当控制系数k1=7,k2=-2,k3=9,k4=-1时,图5为其同步误差曲线,同步时间约为5s;当其控制系数k1=-1,k2=-2,k3=-1,k4=-1时,图6为其同步误差曲线,同步时间约为4s.由此可知,这种同步方法不但实现了异结构混沌系统的同步,而且在同步过程中保留了驱动系统的非线性特性.同时,通过调节控制系数,可提高同步收敛速度,使得驱动系统和响应系统能够快速精确达到同步.

图5 当k1=7,k2=-2,k3=9,k4=-1时的同步误差曲线Fig.5 Curves of synchronization errors when k1=7,k2=-2,k3=9,k4=-1

图6 当k1=-1,k2=-2,k3=-1,k4=-1时的同步误差曲线Fig.6 Curves of synchronization errors when k1=-1,k2=-2,k3=-1,k4=-1
3 结 论
提出了一个含有双曲函数非线性项的四维超混沌系统,通过对该系统的一些基本动力学特性进行数值模拟和理论分析发现,此超混沌系统在参数变化时具有混沌和超混沌等复杂动力学行为,为应用于保密通信等领域提供了选择.同时本文在文献[5]的基础上,给出了一个不删除驱动系统非线性项的异结构混沌同步方法,并给予了严格数学证明.数值模拟结果与理论分析的一致性表明了该改进的同步方法的有效性和可行性.
[1] SMAOUI N,KAROUMA A,ZRIBI M.Secure communications based on the synchronization of the hyperchaotic Chen and the unified chaotic systems[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(8):3279-3293.
[2] R¨OSSLER O E.An equation for hyperchaos[J].Physics Letters A,1979,71(2/3):155-157.
[3] 王光义,郑艳,刘敬彪.一个超混沌Lorenz吸引子及其电路实现[J].物理学报,2007,56(6):3113-3120.WANG Guan-yi,ZHENG Yan,LIU Jing-biao.A hyperchaotic Lorenz attractor and its circuit implementation[J].Acta Physica Sinica,2007,56(6):3113-3120.(In Chinese)
[4] 刘扬正.超混沌Lü系统的电路实现[J].物理学报,2008,57(3):1439-1443.LIU Yang-zheng.A new hyperchaotic Lüsystem and its circuit realization[J].Acta Physica Sinica,2008,57(3):1439-1443.(In Chinese)
[5] 周平,危丽佳,程雪峰.只有一个非线性项的超混沌系统[J].物理学报,2009,58(8):5201-5208.ZHOU Ping,WEI Li-jia,CHENG Xue-feng.A hyperchaos system with only one nonlinear term[J].Acta Physica Sinica,2009,58(8):5201-5208.(In Chinese)
[6] PECORA L M,CARROLL T L.Synchronization in chaotic systems[J].Physical Review Letters,1990,64(8):821-824.
[7] LAN Y,LI Q.Chaos synchronization of a new hyperchaotic system[J].Applied Mathematics and Computation,2010,217(5):2125-2132.
[8] WANG F Q,LIU C X.Synchronization of hyperchaotic Lorenz system based on passive control[J].Chinese Physics,2006,15(9):1971-1975.
[9] 王发强,刘崇新.Liu混沌系统的线性反馈同步控制及电路实验的研究[J].物理学报,2006,55(10):5055-5060.WANG Fa-qiang,LIU Chong-xin.Synchronization of Liu chaotic system based on linear feedback control and its experimental verification[J].Acta Physica Sinica,2006,55(10):5055-5060.(In Chinese)
[10]LIU Y Z,JIANG C S,LIN C S,et al.Chaos synchronization between two different 4Dhyperchaotic Chen systems[J].Chinese Physics,2007,16(3):660-665.
[11]HUA C C,GUAN X P.Synchronization of chaotic systems based on adaptive observer design[J].Chinese Physics,2004,13(9):1391-1395.
[12]杨涛,邵惠鹤.一类混沌系统的同步方法[J].物理学报,2002,51(4):742-748.YANG Tao,SHAO Hui-he.Synchronization of a class of chaotic systems[J].Acta Physica Sinica,2002,51(4):742-748.(In Chinese)
[13]LI X F,LEUNG A C S,HAN X P,et al.Complete(anti-)synchronization of chaotic systems with fully uncertain parameters by adaptive control[J].Nonlinear Dynamics,2011,63(1/2):263-275.
[14]BOWONG S.Adaptive synchronization of chaotic systems with unknown bounded uncertainties via backstepping approach[J].Nonlinear Dynamics,2007,49(1/2):59-70.
[15]ZEMOUCHE A,BOUTAYEB M.Nonlinear-observer-based H∞synchronization and unknown input recovery[J].IEEE Transactions on Circuits and Systems I:Regular Papers,2009,56(8):1720-1731.
[16]WU X J,WANG H,LU H T.Hyperchaotic secure communication via generalized function projective synchronization[J].Nonlinear Analysis:Real World Applications,2011,12(2):1288-1299.
[17]余飞,王春华,尹晋文,等.一个具有完全四翼形式的四维混沌[J].物理学报,2012,61(2):106-115.YU Fei,WANG Chun-hua,YIN Jin-wen,et al.A 4-D chaos with fully qualified four-wing type[J].Acta Physica Sinica,2012,61(2):106-115.(In Chinese)
