预应力型钢混凝土框架试验研究和设计理论＊

熊学玉，高 峰，苏小卒

（1.同济大学建筑工程系，上海 200092；2.同济大学先进土木工程材料教育部重点实验室，上海 200092）

预应力型钢混凝土结构是在预应力混凝土结构中配置轧制或焊接型钢的组合结构，它结合了预应力结构与型钢混凝土结构的优点.国内外已对型钢混凝土结构作了一些研究［1－5］，而对预应力型钢混凝土结构仅作了少量的研究.文献［6－9］通过预应力型钢混凝土简支梁、连续梁的竖向静力实验，对预应力型钢混凝土结构的承载力、裂缝分布与开展及变形发展情况进行了初步研究，实验表明在型钢混凝土梁中施加预应力，能够提高结构构件承载力，较好地改善型钢混凝土梁的抗裂性能，抑制裂缝开展和增加构件的刚度.实际工程大多数为有侧向约束的超静定结构如框架结构等，目前还没有关于约束影响下预应力型钢混凝土框架的实验研究与理论分析.

本文研究有约束的预应力型钢混凝土结构的受力性能特征和设计计算理论，基于两榀大尺度后张有粘结预应力全型钢混凝土框架的静力试验，系统地研究和分析了预应力型钢混凝土框架梁的破坏形态、弯矩调幅、抗裂性能、裂缝分布和变形规律，进而分析次内力产生的本质，提出了考虑次内力包括次弯矩、次轴力的预应力型钢混凝土结构的抗弯极限承载力、抗裂度、刚度及最大裂缝宽度计算公式，计算结果与试验数据吻合较好.本文作为在编国家行业标准《预应力混凝土设计规范》的在研项目，所提计算理论反映了现代预应力设计理论的思想，为规范中“预应力型钢混凝土结构”一章的编制提供依据.

1 预应力型钢混凝土框架试验研究及现象分析

1.1 试验框架概况

为增加试验结果的可信度，试验采用大比例的试验构件，主要考察框架梁控制截面纵向受力筋改变时结构的各项特征.框架柱中线长度为8.2m，构件配置足够的箍筋以防止剪切破坏，XGKJ1纵筋采用6Ф18（HRB400）；XGKJ2纵筋采用6Ф22（HRB400），内置型钢钢材型号为Q235，梁中型钢为Ι290×100×8×10，柱型钢为Ι280×120×8×14，连接螺栓M20为8.8级摩擦性高强螺栓.柱内型钢上下翼缘、梁端型钢上翼缘设两排Ф19＠200栓钉.试验构件配筋及型钢节点连接如图1所示.

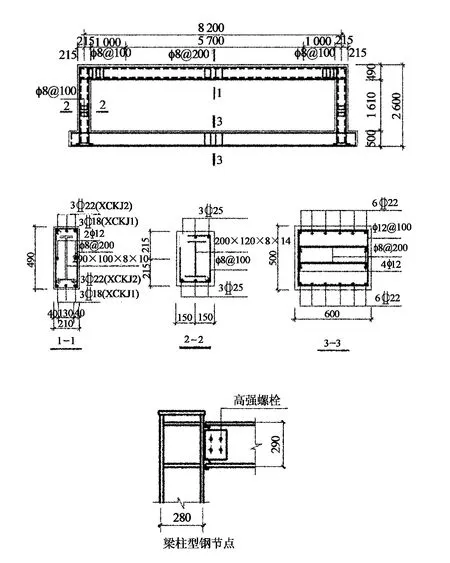
图1 XGKJ1，2试验框架基本尺寸及配筋详图Fig.1 Dimensions and reinforcements of specimen XGKJ1，2

预应力筋均为2Φs15.2（fptk＝1 860N／mm2）的高强钢绞线，沿梁长三段抛物线布置，反弯点距梁两端各0.1倍梁轴跨处（定位详见图2）.预应力筋的张拉控制应力为0.75fptk，张拉端采用单孔OVM两夹片式锚具，锚具下安置压力传感器用于测量有效张拉力.混凝土、钢筋、钢绞线、型钢材料的力学性能见表1和表2.

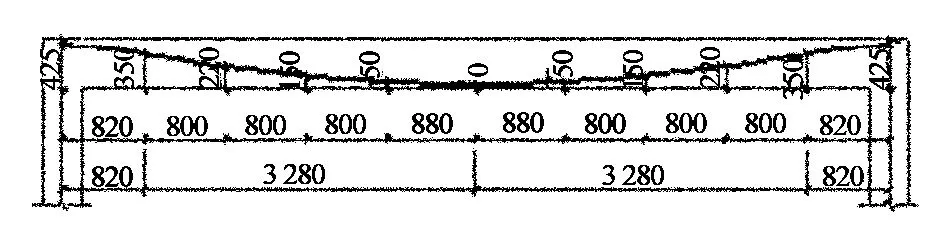
图2 XGKJ1，2预应力钢铰线曲线定位图Fig.2 Lay out of pre－stressed wire curve of XGKJ1，2

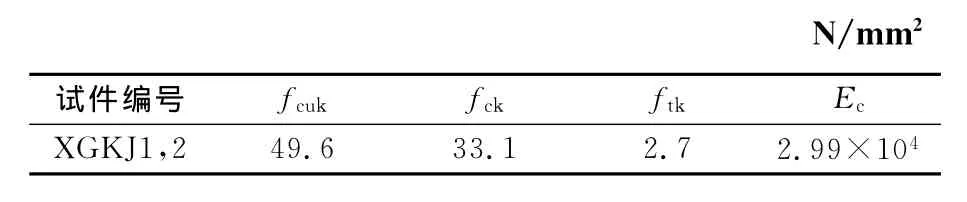
表1 混凝土的力学性能Tab.1 Mechanical properties of concrete for specimens

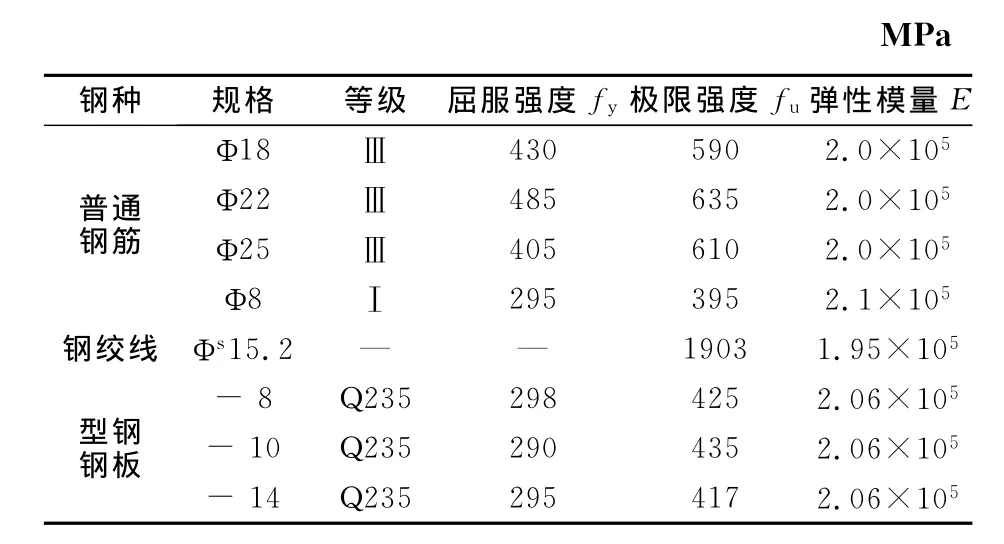
表2 钢绞线、型钢及钢筋的力学性能Tab.2 Mechanical properties of materials for specimens

1.2 试验加载方案

试验框架采用三分点集中对称的同步分级加载方式.跨中纯弯段长度为2 700mm.在反力架钢梁下，依次设传感器、千斤顶等.试验框架加载实景如图3所示.

荷载的施加：开裂前，以框架梁端计算开裂荷载Pcr为参照，每级荷载约为0.1Pcr，开裂后，按每级20kN逐步加载至跨中受拉钢筋屈服，每加一级荷载后，持荷10min，荷载稳定后采集数据.受拉钢筋屈服后，持续加载至框架破坏.

图3 试验全貌Fig.3 General view of the test

1.3 试验现象描述

在加载过程中，两榀框架首先在梁端开裂，然后跨中、柱顶外侧开裂.加载到40kN左右时，框架梁端上部出现首批裂缝，随着荷载的增加，跨中底部、柱顶相继出现裂缝.加载到0.5Pu左右时裂缝已经基本出齐.当两榀框架接近极限荷载时，由于框架梁内型钢的粘结滑移，则梁跨中纯弯段侧面型钢下翼缘附近有水平裂缝出现并逐步展开.两榀框架梁的端部产生塑性铰，最后跨中上部受压区混凝土压碎破坏，发生了类似适筋梁的延性破坏.图4为框架极限破坏时裂缝分布图，图5～图8为框架节点梁跨中破坏图片.

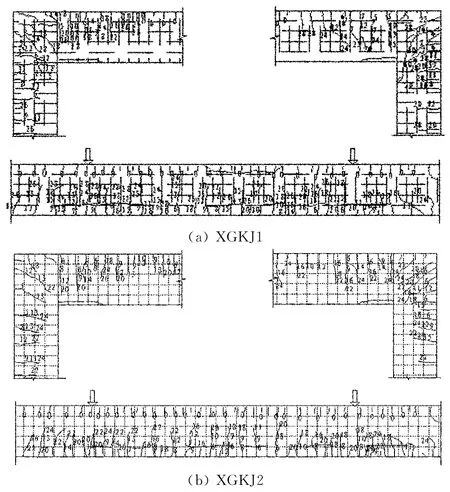
图4 极限破坏时XGKJ1，XGKJ2梁端和跨中裂缝分布图（×10kN）Fig.4 Crack distribution of XGKJ1and XGKJ2 at ultimate failure（×10kN）

图5 XGKJ1框架梁端、结点破坏Fig.5 Frame beam damage in middle span

图6 XGKJ1框架梁跨中破坏Fig.6 Frame damage of girder end

图7 XGKJ2框架梁左端结点破坏Fig.7 Frame damage of left girder end

图8 XGKJ2框架梁右端结点破坏Fig.8 Frame damage of right girder end

1.4 荷载－跨中挠度曲线

由图9可看出，预应力型钢混凝土框架梁跨中变形有2个显著特点：1）当框架梁达到开裂荷载后，不因混凝土的开裂而在荷载挠度曲线上出现明显的转折点.这是因为框架梁受拉区裂缝开展到钢骨受拉翼缘水平处，由于受到刚度较大型钢的约束以及预应力的作用，裂缝几乎不再向上发展，宽度增加也不大，产生了裂缝开展“停滞”现象.2）在使用阶段梁的刚度降低较少，比较接近直线关系，钢筋与型钢的屈服大致上同步.钢筋屈服后出现塑流，变形增大，型钢与混凝土产生较大的相对滑移后对混凝土的有效约束减小，导致框架梁的变形急剧增大.

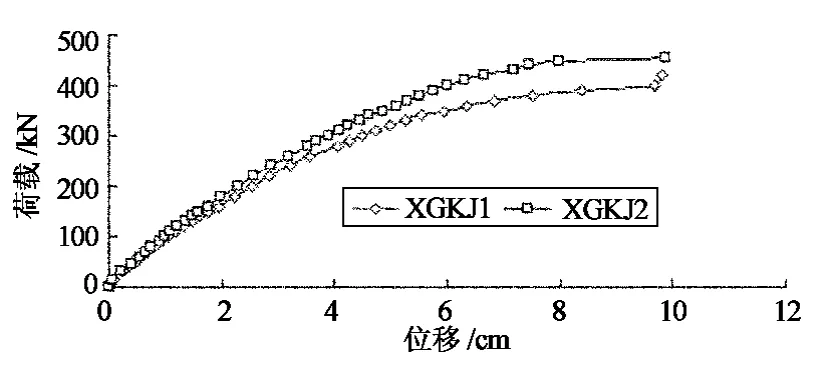
图9 框架荷载－跨中挠度曲线Fig.9 Load－deflection curve in middle span

1.5 延性分析

延性是结构在其承载能力没有明显下降的情况下，承受屈服后非弹性变形的能力.延性在超静定结构的塑性内力重分布中起重要作用，它使超静定结构所承受的弯矩由某一控制截面向其他控制截面转移，因此，延性是评价结构优劣的一个重要指标.以关键截面框架梁端非预应力受拉钢筋屈服为形成塑性铰的标志，取结构梁端受拉钢筋屈服时的挠度为fe，取结构达到极限荷载时的挠度为极限挠度fu，计算出框架的位移延性比，见表3.预应力型钢混凝土框架梁的延性位移比大于3满足规范要求.

表3 XGKJ1，XGKJ2位移延性比Tab.3 Deflection ductility of XGKJ1，XGKJ2

2 预应力型钢混凝土框架梁抗弯承载力及弯矩调幅计算

2.1 约束及其分布的本质

在预应力混凝土结构中，构件预应力筋的张拉将使其发生轴向压缩变形.如果该结构为静定结构，构件变形不会受到约束作用，截面内混凝土预压应力合力作用线与预应力钢筋的合力作用线重合，从而保持平衡状态.若是超静定结构，预应力构件的变形会受到多余约束的限制，从而在相关构件中产生次内力.对于无侧向约束的超静定结构，如预应力连续梁结构，预应力构件在支座处的竖向变形受到约束，并在构件中各截面处产生次弯矩和次剪力.但如果是有侧向约束的预应力超静定结构，如框架结构、剪力墙结构、筒体结构等，由于构件张拉时的轴向变形受到竖向构件的阻碍作用，预应力构件中除了产生次弯矩和次剪力外，还会产生表现为拉力的次轴力，并在与之相连的竖向构件中产生相应的次内力，这将对预应力混凝土结构的设计产生影响.故约束及其分布是产生次内力的本质.约束引起的次轴力使受弯构件变成拉弯构件，对构件的承载能力、裂缝、刚度产生不利影响.中国现行预应力混凝土结构的设计理论是基于预应力混凝土连续梁的工作原理建立起来的，因而对于无侧向约束的结构来说是合理的，对于有侧向约束的工程，若侧向约束不大，则其结果可以接受；若结构侧向约束较大却不加以考虑，则可能会造成这些构件的承载力计算值大于实际值，挠度及裂缝宽度计算值较实际值小，从而造成安全隐患［10］.有约束影响预应力结构设计时应考虑约束对预应力效应的影响，次轴力作用采用作用在换算截面重心位置的次轴力N2进行计算［11］.全面考虑次内力影响的预应力设计理论使预应力混凝土结构设计的经典方法得到改进和完善.

2.2 预应力型钢混凝土框架梁抗弯承载力计算

参照GB 50010—2010《混凝土结构设计规范》［12］和《型钢规程》［13］，基于平截面假定，与钢筋混凝土梁的计算类似，考虑预应力超静定结构次内力，建立预应力型钢混凝土梁的抗弯承载力计算公式.

2.2.1 界限压区高度

普通钢筋、预应力钢筋和型钢受拉翼缘屈服时，受压区高度的最小值可以认为是预应力型钢混凝土梁的截面界限压区高度，如图10所示，设普通钢筋、预应力钢筋和型钢受拉翼缘屈服时，受压区高度分别为xs，xp，xa.

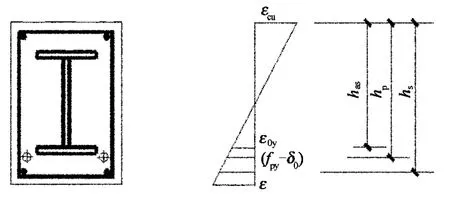
图10 界限受压区高度计算简图Fig.10 High limits of compression zone

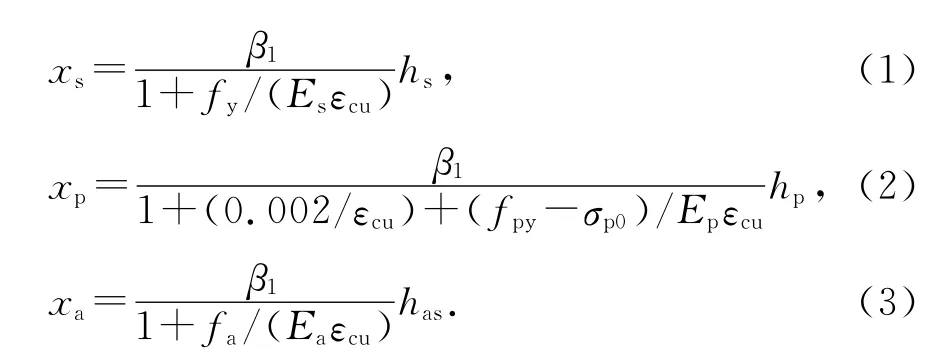
2.2.2 正截面承载力计算

如图11框架梁正截面受弯承载力计算简图所示，由Σx＝0得下式：

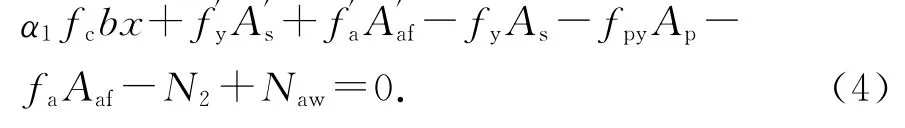
极限弯矩为：

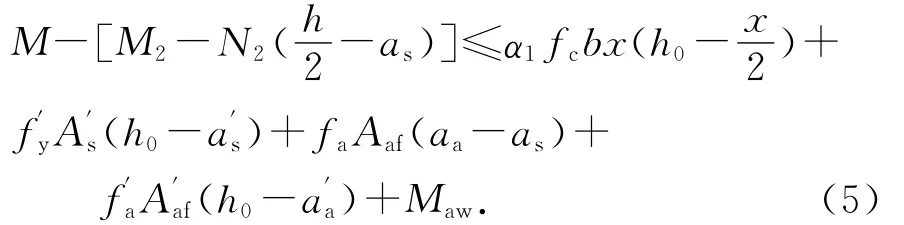
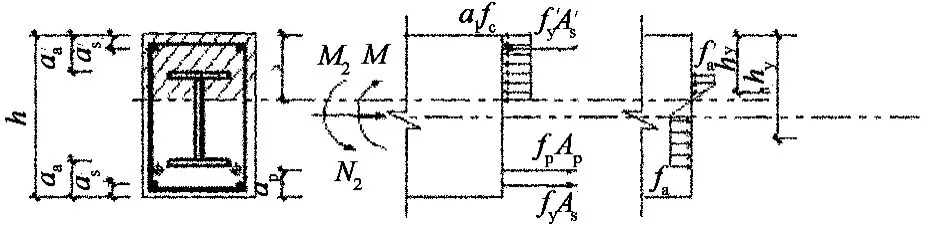
图11 框架梁正截面受弯承载力计算简图Fig.11 Bending bearing capacity calculation diagram

当δ1h0＜1.25x，δ2h0＞1.25x时，

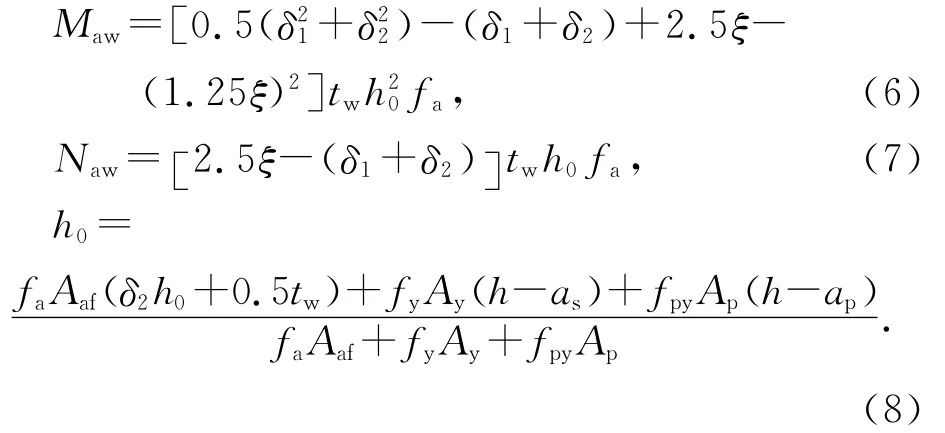
混凝土受压区高度x尚应符合下列公式要求：

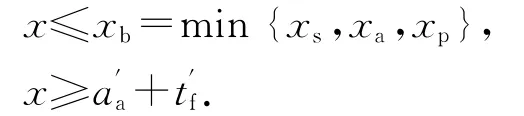
式中：b为梁宽；aa，分别为型钢下翼缘至受拉区截面边缘及钢骨上翼缘至受压区截面边缘的距离；tw为型钢腹板厚度；As，，Ap分别为受拉钢筋、受压钢筋与预应力筋的截面积；Aaf，分别为型钢下翼缘与上翼缘截面积；fy，，fpy分别为受拉钢筋、受压钢筋、预应力筋强度设计值；fa为型钢强度设计值；δ1为型钢腹板上端至截面上边距离与h0的比值；δ2为型钢腹板下端至截面上边距离与h0的比值；Maw为型钢腹板承受的轴向合力对型钢受拉翼缘、预应力筋和纵向受拉钢筋合力点的力矩；Naw为型钢腹板承受的轴向合力；h0为型钢受拉翼缘、纵向受拉钢筋和预应力筋合力点至混凝土受压边缘距离.

2.2.3 理论值与试验值的对比

首先利用公式算出预应力型钢混凝土框架梁的截面极限弯矩，利用结构力学的超静定结构极限荷载的方法［14］对XGKJ1，XGKJ2屈服荷载和极限荷载进行计算对比，理论计算结果和试验实测结果见表4.计算结果与试验值均吻合较好.

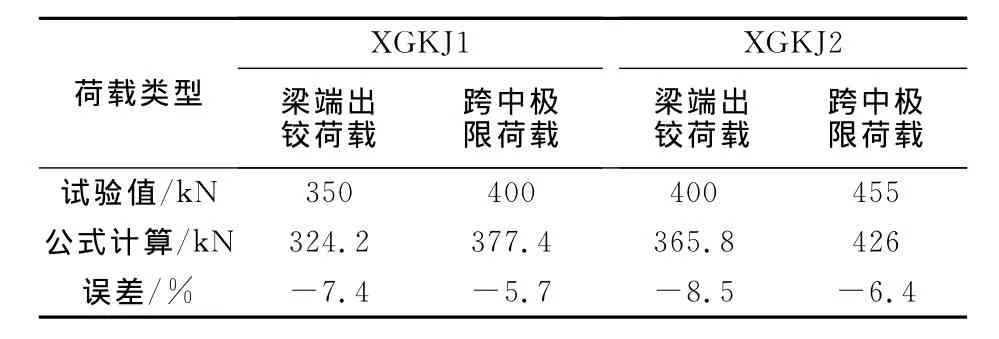
表4 XGKJ1，XGKJ2试验荷载值与理论计算值对比Tab.4 Theoretical values comparison with test values

2.3 弯矩调幅

把初始次弯矩当作一种不变弯矩，这样总调幅β就被分作两部分，即荷载调幅βload和次弯矩调幅βsec，具体计算公式如下［15－16］：

式中：Mload为框架梁破坏时按弹性计算的梁端截面的弯矩；Mu为框架梁端截面的极限弯矩；Msec为框架梁端截面的总次内力弯矩，包括两部分：第1部分为次弯矩Msec1，第2部分为次轴力引起的次轴力弯矩Msec2.根据上式，将XGKJ1，2的Mload，Mu和Msec计算值列于表5.

表5 XGKJ1，2弯矩调幅计算表Tab.5 Moment modification of XGKJ1，2

由表5中可以看出，预应力型钢混凝土框架弯矩调幅值为30%左右，通过文献［15－16］实验研究，后张有粘结预应力混凝土结构框架结构的调幅一般不超过20%.故预应力型钢混凝土框架结构调幅值比普通后张有粘结预应力混凝土结构框架结构提高10%.次内力在预应力框架结构的弯矩调幅中起着比较重要的作用，由于次弯矩的方向与外荷载负弯矩方向相反，次弯矩相当于减小了柱顶截面的弯矩值，符合常规设计中调小关键截面弯矩设计值这一调幅原则，因此次弯矩对柱顶调幅作用有利.

3 预应力型钢混凝土结构的正常使用极限状态计算理论

3.1 抗裂度计算

考虑框架结构次轴力、次弯矩影响，预应力型钢混凝土框架梁的开裂弯矩计算公式为：

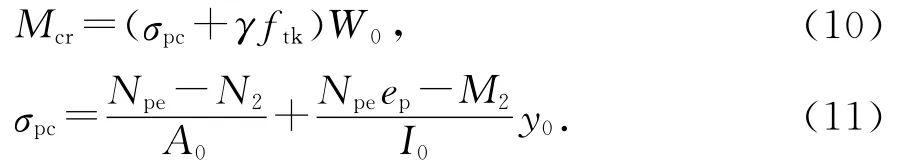
式中：σpc为扣除全部预应力损失后在抗裂验算边缘的混凝土法向应力，MPa；I0，W0，y0分别为换算截面的惯性矩、弹性抵抗矩、换算截面重心至所计算纤维处的距离；M2，N2分别为框架次弯矩、次轴力；γ为混凝土构件的截面抵抗矩塑性影响系数，对于预应力型钢混凝土梁，由于型钢的存在，混凝土的收缩和徐变会使构件混凝土中产生拉应力，降低构件的抗裂能力，建议取γ＝1.0.表6为开裂弯矩理论计算值与试验值对比.

表6 开裂弯矩理论计算值与试验值对比Tab.6 Comparison of crack moment of calculated and test values

由表6可以看出，试验值与理论值较吻合，公式能满足工程需要.

3.2 挠度计算

预应力混凝土受弯构件的挠度由使用荷载产生的下挠度（f1）和预应力引起的上挠度（又称反拱挠度f2）两部分组成，则预应力型钢混凝土框架跨中的总挠度为：f＝f1－f2.预应力型钢混凝土结构刚度为构成该结构的预应力钢筋混凝土刚度与型钢刚度之间的叠加［17］，其中预应力钢筋混凝土刚度由GB 50010—2010《混凝土结构设计规范》［12］确定.预应力型钢混凝土结构截面抗弯刚度为：

1）要求不出现裂缝构件的刚度

2）允许出现裂缝构件的刚度

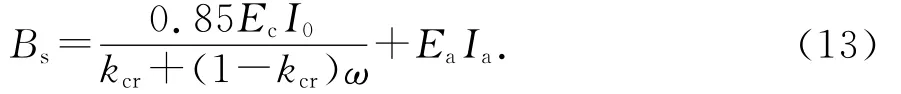
式中：kcr＝Mcr／Mk，Mcr为开裂弯矩，考虑次轴力影响见3.1公式推导；I0为换算截面惯性矩，不包括型钢部分；Ea和Ia分别为内置型钢弹性模量和惯性矩.其余未注明符号均同GB 50010—2010《混凝土结构设计规范》［12］.

XGKJ1，XGKJ2框架梁跨中挠度公式计算值与试验值对比图如图12和图13所示.

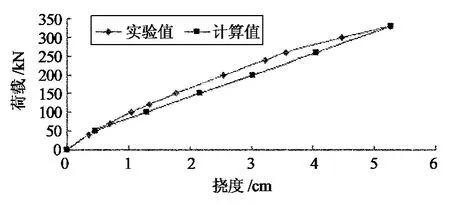
图12 XGKJ1荷载－挠度曲线Fig.12 Load－deflection curve of XGKJ1

从图12与图13可知，在正常使用条件下，预应力型钢框架梁的挠度理论计算值与试验值较吻合.

3.3 裂缝宽度计算

把型钢翼缘作为纵向受力钢筋，且考虑部分型钢腹板的影响，以混凝土结构设计规范中预应力结构裂缝宽度的计算公式为基础，并考虑侧向约束的影响，在计算Mcr，σsk时考虑次弯矩和次轴力.参照GB 50010—2010《混凝土结构设计规范》［12］计算方法，预应力型钢混凝土结构最大裂缝计算公式如下：

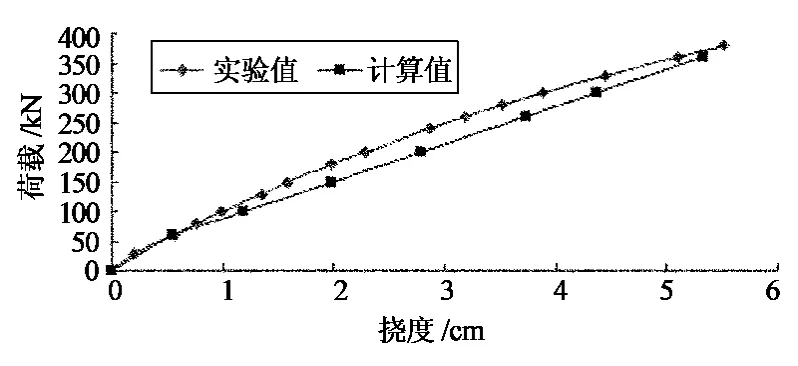
图13 XGKJ2荷载－挠度曲线Fig.13 Load－deflection curve of XGKJ2

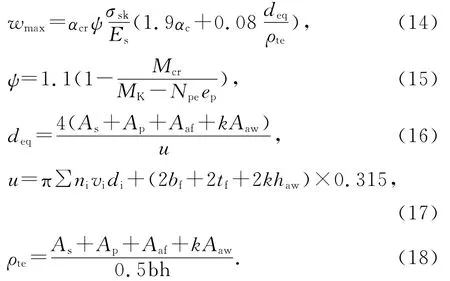
式中：构件受力特征系数αc＝1.7；vi为受拉区第i种纵向钢筋的相对粘结特性系数，型钢的相对粘结特性系数为0.45×0.7＝0.315［18］；ep为预应力钢筋作用重心到截面重心轴的距离；Aaf，Aaw分别为型钢受拉翼缘、腹板的截面面积；bf，tf分别为型钢受拉翼缘宽度、厚度；haw为腹板高度；k为型钢腹板影响系数，等于梁受拉侧1／4梁高范围内腹板高度与整个腹板高度的比值.其余未注明符号意义同GB 50010－2010《混凝土结构设计规范》［12］.

在有侧向约束的预应力混凝土框架结构中，次轴表现为拉力，从而使得框架梁成为预应力混凝土偏心受拉构件.考虑次轴力时，裂缝宽度计算截面内力图如图14所示，由截面内力平衡计算的σsk如下：

由图14（b），对截面受压中心取矩：

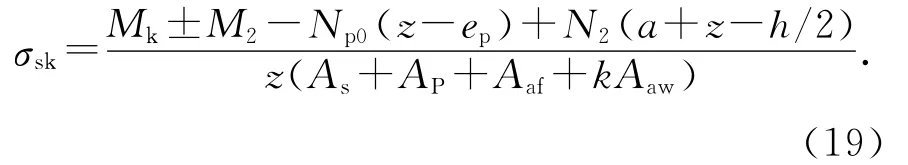
由图14（b）（c），轴向压力作用点至纵向受拉钢筋合力点的距离e为：

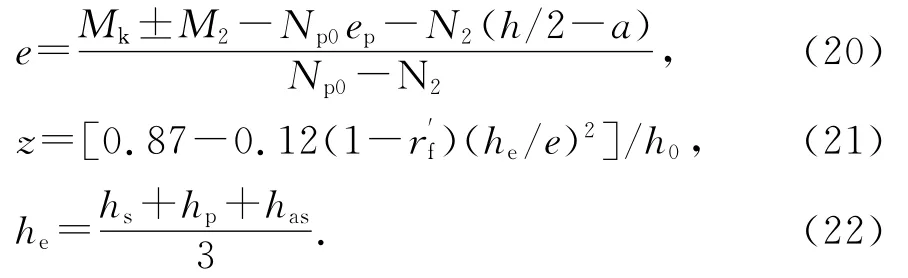
式中：he为受拉区钢筋等效高度；hs，hp，has符号意义见图10；a为纵向受拉钢筋合力点至受拉边距离.其余未注明符号意义同GB 50010－2010《混凝土结构设计规范》［12］.表7为裂缝宽度理论计算值与试验值对比.

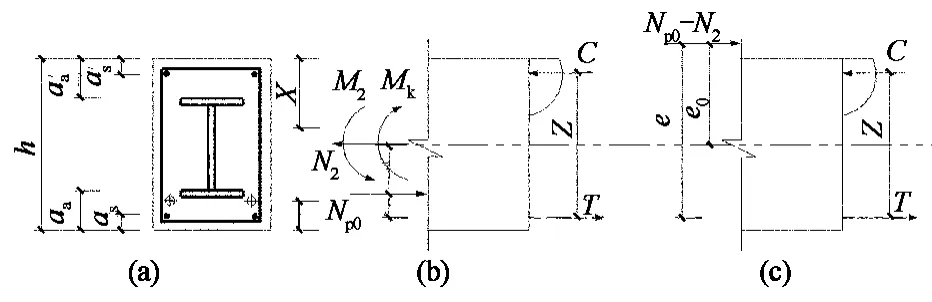
图14 裂缝宽度计算应力图Fig.14 Calculation stress diagram of crack width

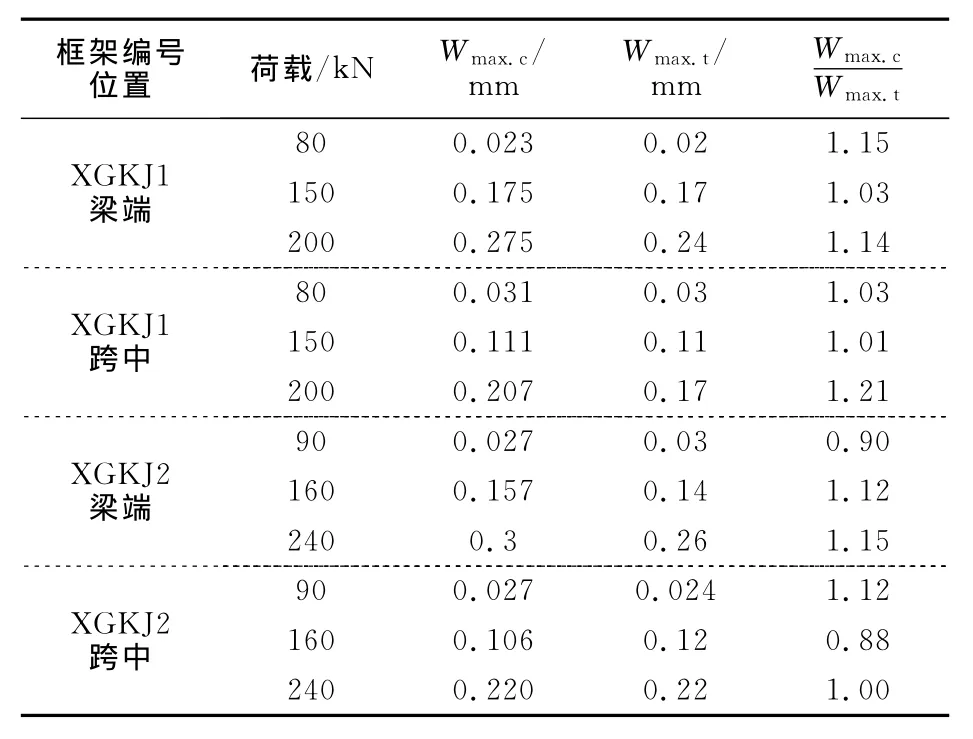
表7 裂缝宽度理论计算值与试验值对比Tab.7 Comparison of crack width between calculated values and test results

裂缝宽度理论计算值与试验值的比值为1.08±0.10，说明理论公式具有较高的精度，可用于计算正常使用阶段预应力型钢混凝土框架梁的最大裂缝宽度.

4 结 论

1）预应力型钢混凝土框架梁发生类似于钢筋混凝土适筋梁的正截面受弯破坏，属延性破坏.结构中型钢和预应力的存在，抑制了裂缝的开展，受力筋屈服前，使构件在荷载增加的情况下出现了裂缝发展的“停滞”现象，这种现象使框架梁达到开裂荷载后，不因混凝土的开裂而在荷载挠度曲线上出现明显的转折点.

2）试验构件梁端形成塑性铰实现了塑性内力重分布，位移延性比大于3，弯矩调幅值为30%左右，弯矩调幅值比普通后张有粘结预应力混凝土结构框架结构提高10%左右，实际设计中可以对预应力型钢混凝土框架梁端进行适当的弯矩调幅设计.

3）约束及其分布是产生次内力的本质，在侧向约束较大的预应力超静定结构中，次轴力产生的不利影响不能忽略，所以在预应力型钢混凝土结构计算理论中，不仅要考虑次弯矩，还要考虑次轴力.

4）本文提出考虑次内力包括次弯矩、次轴力的预应力型钢混凝土结构的抗弯极限承载力、抗裂度、刚度及最大裂缝宽度计算公式，结果与试验数据较吻合.反映了现代预应力设计理论的思想，为在编预应力混凝土设计规范中“预应力型钢混凝土结构”一章的编制提供依据.

5）本文框架由于框架柱的侧向约束较小，故次轴力的影响不明显，但是预应力型钢混凝土结构一般应用于大跨、超长结构中，如果不考虑次轴力的影响，可能会导致结构的不安全.

［1］ 李俊华，李玉顺，王建民，等.型钢混凝土柱粘结滑移本构关系与粘结滑移恢复力模型［J］.土木工程学报，2010，43（3）：46－52.LI Jun－hua，LI Yu－shun，WANG Jian－min，et al.Bond－slip constitutive relation and bond－slip resilience model of shapesteel reinforced concrete columns［J］.China Civil Engineering Journal，2010，43（3）：46－52.（In Chinese）

［2］ ROEDER C W.Composite and mixed construction［M］.New York：ASCE，1984.

［3］ 叶列平，方鄂华.钢骨混凝土构件的受力性能研究综述［J］.土木工程学报，2000，33（5）：1－11.YE Lie－ping，FANG E－hua.State－of－the－art of study on the behaviors of steel reinforced concrete structure［J］.China Civil Engineering Journal，2000，33（5）：1－11.（In Chinese）

［4］ MANFREDI G，FABBROCINO G，COSENZA E.Modeling of steel－concrete composite beams under negative bending［J］.Journal of Engineering Mechanics，1999，125（6）：654－662.

［5］ FABBROCINO G，MANFREDI G，COSENZA E.Analysis of continuous composite beams including partial interaction and bond［J］.Journal of Structure Engineering，2000，126（12）：1288－1294.

［6］ 王钧，邬丹，郑文忠.预应力H型钢混凝土简支梁正截面受力性能试验［J］.哈尔滨工业大学学报，2009，41（6）：22－27.WANG Jun，WU Dan，ZHENG Wen－zhong.Experimental research on flexural mechanical behavior of simple prestressed H－steel reinforced concrete beam［J］.Journal of Harbin Institute of Technology，2009，41（6）：22－27.（In Chinese）

［7］ 傅传国，李玉莹，梁书亭.预应力型钢混凝土简支梁受弯性能试验研究［J］.建筑结构学报，2007（6）：62－73.FU Chuan－guo，LI Yu－ying，LIANG Shu－ting.Experimental study on simply supported prestressed steel reinforced concrete beams［J］.Journal of Building Structures，2007（6）：62－73.（In Chinese）

［8］ 李峰.预应力钢骨混凝土梁承载能力试验研究［D］.重庆：重庆大学土木工程学院，2007.LI Feng.Experimental research on the carrying capacity of the prestressed steel reinforced concrete beam［D］.Chongqing：Chongqing University，College of Civil Engineering，2007.（In Chinese）

［9］ 郑文忠，王钧，韩宝权，等.内置H型钢预应力混凝土连续组合梁受力性能试验研究［J］.建筑结构学报，2010（7）：23－31.ZHENG Wen－zhong，WANG Jun，HAN Bao－quan，et al.Experimental research on mechanical behavior of continuous prestressed composite concrete beams with encased H－steel［J］.Journal of Building Structures，2010（7）：23－31.（In Chinese）

［10］张德峰，吕志涛.侧向约束对预应力混凝土框架压力的影响［J］.建筑结构，2001，31（5）：51－52.ZHANG De－feng，LV Zhi－tao.Effect of lateral restraints on the transfer of compressive force in frame structures［J］.Building Structures，2001，31（5）：51－52.（In Chinese）

［11］熊学玉，张彩红，吴学淑.约束（侧向）对预应力结构设计影响的研究［J］.建筑结构，2006，36（11）：88－90.XIONG Xue－yu，ZHANG Cai－hong，WU Xue－shu.Study on lateral restraint in prestressed structure［J］.Building Structures，2006，36（11）：88－90.（In Chinese）

［12］GB 50010—2010 混凝土结构设计规范［S］.北京：中国建筑工业出版社，2010.GB 50010—2010 Code for design of concrete structures［S］.Beijing：China Architecture ＆Building Press，2010.（In Chinese）

［13］JGJ 138—2001 型钢混凝土组合结构技术规程［S］.北京：中国建筑工业出版社，2001.JGJ 138—2001 Technical specification for steel reinforced concrete composite structures［S］.Beijing：China Architecture ＆Building Press，2001.（In Chinese）

［14］龙驭球，包世华.结构力学教程［M］.北京：高等教育出版社，1988：116－126.LONG Yu－qiu，BAO Shi－hua.Structural mechanics tutorial［M］.Beijing：Higher Education Press，1988：116－126.（In Chinese）

［15］简斌，王正霖，白绍良.预应力混凝土连续梁弯矩调幅建议［J］.重庆建筑大学学报，1999，21（2）：12－18.JIAN Bin，WANG Zheng－lin，BAI Shao－liang.Suggestions for moment modulation of prestressed concrete continuous beam［J］.Journal of Chongqing Jianzhu University，1999，21（2）：12－18.（In Chinese）

［16］简斌，孙新敏，王正霖.后张有粘结预应力混凝土框架弯矩调幅的试验［J］.重庆大学学报，2004，27（4）：107－110.JIAN Bin，SUN Xin－min，WANG Zheng－lin.Experimental study on moment modulation of prestressed frames［J］.Journal of Chongqing University，2004，27（4）：107－110.（In Chinese）

［17］赵世春，施建平.型钢混凝土梁受弯刚度计算［J］.西南交通大学学报，2004，39（6）：730－733.ZHAO Shi－chun，SHI Jian－ping.Computation of flexural rigidity of steel reinforced concrete beam［J］.Journal of Southwest Jiaotong University，2004，39（6）：730－733.（In Chinese）

［18］白国良，姜维山，赵鸿铁.型钢混凝土梁的裂缝宽度计算［J］.西安建筑科技大学学报，1995，27（3）：320－328.BAI Guo－liang，JIANG Wei－shang，ZHAO Hong－tie.Calculation crack width on SRC beam［J］.Journal of Xi＇an University of Architecture ＆Technology，1995，27（3）：320－328.（In Chinese）