气-液两相在多孔介质内同向向上流动的CFD研究*
2012-03-06王宏涛廖永浩龚光彩
余 健,王宏涛,廖永浩,龚光彩
(1.湖南大学土木工程学院,湖南长沙 410082; 2.91024部队,广东台山 529266;3.华电电力科学研究院,浙江杭州 310030)
气-液两相在多孔介质内同向向上流动的CFD研究*
余 健1†,王宏涛1,2,廖永浩3,龚光彩1
(1.湖南大学土木工程学院,湖南长沙 410082; 2.91024部队,广东台山 529266;3.华电电力科学研究院,浙江杭州 310030)
基于计算流体力学中欧拉模型,研究了气-液两相在球形多孔介质填充床内同向向上流动情况.分别采用Tung &Siefken模型、Schulenberg模型以及Attou模型通过用户自定义功能的形式添加气固、液固、气液间曳力程序对填充床流动情况进行CFD三维数值模拟.对其模拟结果与实测数据进行对比发现:Tung &Siefken的模型更适合模拟在常温常压下直径在2~8 mm的球形多孔介质内气-液两相流流动,此模型CFD数值模拟的压降差、持液量结果均与实测数据吻合很好.
欧拉模型;气-液两相流;多孔材料;数值模拟
在现代许多工程技术领域中,比如在核电工业的核反应堆、石油化工的固化床和流化床、环境工程的脱硫塔、曝气生物滤池和滴滤池中,都存在大量关于多孔介质内气-液两相流动问题[1-5].因此,开展多孔介质内气-液两相流动的研究,具有十分重要的意义.
目前,国内外对于多孔介质内气-液两相流动的研究多为理论分析和实验研究,且大部分研究都集中在气-液同向向下流动,而对气-液同向向上流动的研究较少,应用计算流体力学(CFD)三维数值模拟气-液同向向上流动还尚未见报导.Chu[1]等在试验的基础上研究玻璃球床内空气和水两相向上流动,主要研究多孔介质粒径、轴线床层孔隙率的变化、气液流量对压降和持液量影响.Schulenberg[2]等在实验基础上,在粗碎片多孔介质内考虑蒸汽与液体间曳力,提出了多孔介质内多相流压降和持液量模型.Tung等[3]在多孔介质内两相流实验的基础上,提出泡状流等不同流态概念并建立了一维压降预测和持液量模型.Molga等[4]研究了在高压下吸收塔内CO2气体与液相流动,考虑了系统压力、气相和液相表观速度、液相粘度以及多孔介质粒径对压降和持液量影响.Schmidt[5]通过总结大多数学者关于多孔介质内气液同向向上流动的压降模型,并在大量实验基础上提出了自己的压降和持液量模型,但通用性不强.
本文首次应用CFD三维数值模拟在常温常压下球形多孔介质内空气和水的两相流流动,分别采用Tung &Siefken模型,Schulenberg模型以及Attou模型定性分析气液流量和多孔介质粒径对压降的影响,利用CFD对多孔介质内气-液两相同向向上流动进行三维数值模拟以确定最佳模型.
1 数学模型
1.1 模型假设
在常温常压下气-液两相同向向上流过多孔介质,气体为空气,液相为去离子水,做如下假设:
1)气相与液相间无相变发生;
2)固定床内的多孔介质固定不动;
3)球形多孔介质被液体完全湿润,毛细压力可忽略;
4)球形多孔介质被视为各向同性,不考虑轴向床层内孔隙率的变化;
5)不考虑多孔介质的“壁面效应”;
6)气体为不可压缩流体.
1.2 体积分率连续性方程
当气-液两相流流过球形多孔介质时,每一个孔隙都由气相与液相共同占有,即

式中:G为气相;L为液相;ε为孔隙率.
1.3 质量守恒方程(连续性方程)
气相与液相流体均满足如下质量守恒方程:
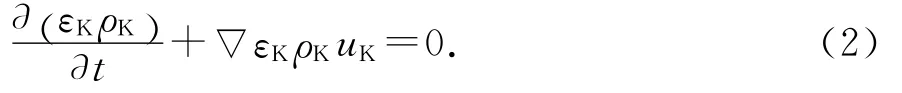
式中:下标K代表相,气相K=G,液相K=L.
1.4 动量守恒方程
气相与液相流体均满足如下动量守恒方程:
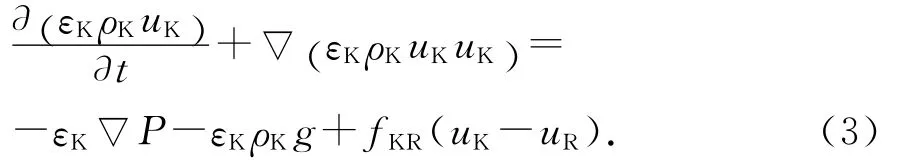
式中:εK为K相的体积分数;ρK为K相的密度;uK为K相的真实物理速度;P为压力;fKR为K相与其他相动量交换系数.
1.5 NS方程封闭模型
多孔介质内单相流一般通过Ergun[6]公式考虑流体与多孔介质颗粒之间的粘性和惯性作用来实现Navie-Stokes方程的封闭.有些学者[1-2]认为:多孔介质内两相流动,由于一相流体的流动影响另外一相的渗透率和通过率,建议直接对Ergun公式进行修正以应用于多孔介质内两相流动的研究,引入相对渗透率和相对通过率2个变量,即相对渗透率模型.不同学者提出不同的相对渗透率模型,但其模型应用于数值模拟的可行性还需进一步研究.
1.5.1 Tung &Siefken相对渗透率模型
结合单相Kozeny-Carman方程,多相流中气固动量交换系数的通用表达形式为:
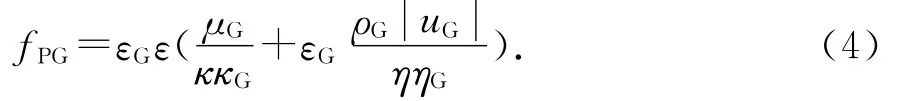
式中:κG为气相相对渗透率;ηG为气相相对通过率;绝对渗透率κ和绝对通过率η采用Ergun公式[7]求得:
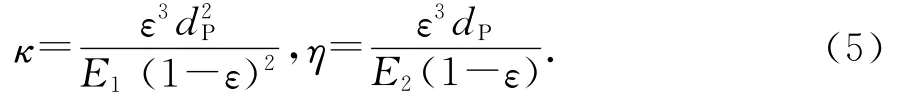
式中:E1和E2为Ergun系数,本文中分别取150和1.75.
Tung根据泡状流,泡状到弹状过渡流,弹状流,弹状到柱状过渡流以及柱状流提出对应流态的相对渗透率和相对通过率[3].


式中:αL为持液量;κL为液相相对渗透率;ηL为液相相对通过率.
多孔介质内气相与液相由于相对运动从而产生相互作用曳力,其值的确定在国际上一直是难点.Schulenberg[2],Tung[3],Schmidt[5],Attou[8]等提出了不同的气液曳力模型.Tung认为当流态为泡状流和弹状流时,气相以单一分散气泡的形式在多孔介质内运动;在较低流速(Stokes流)时,粘性力在气泡与液相间曳力中占主导地位;在较高流速时,曳力主要来自惯性力.综合考虑粘性力与惯性力,提出下面的曳力系数表达式[3]:
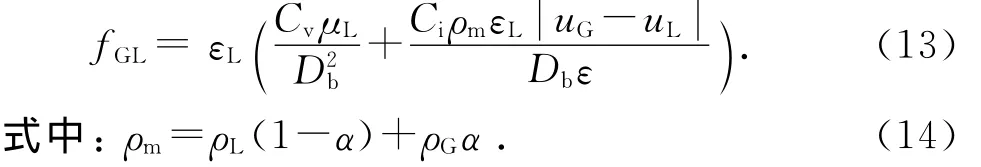
Tung在试验的基础上,根据泡状流和弹状流提出对应流态的粘性系数C和惯性系数C[3].
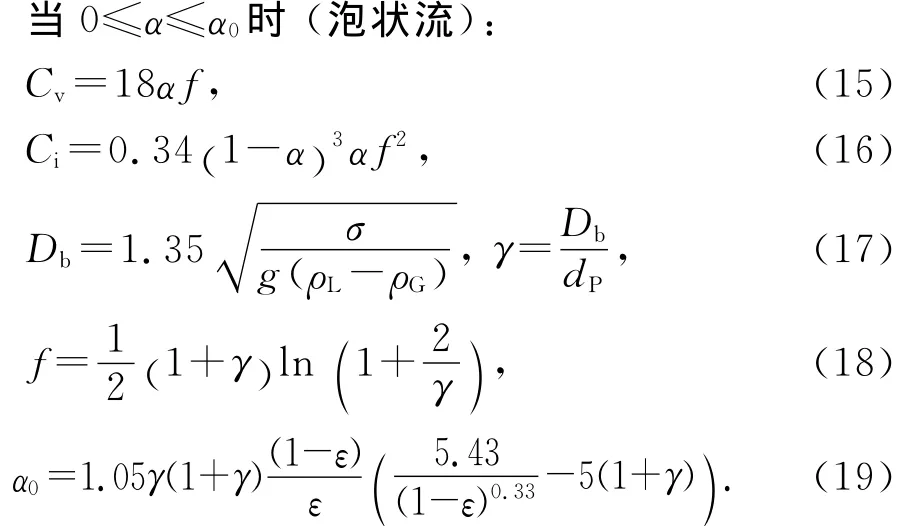
式中:γ为气泡与颗粒直径比;σ为表面张力;f为形状影响因子;dP为多孔介质当量粒径.


关于弹状到柱状过渡流和柱状流,Tung认为弹状气泡合并在一起形成气相连续相在通道流动,而液相以液滴的形式流动[3],其气液曳力系数表达式分别为式(28)和式(29).

式中:κG和ηG采用式(7)计算;W采用公式(8)计算.
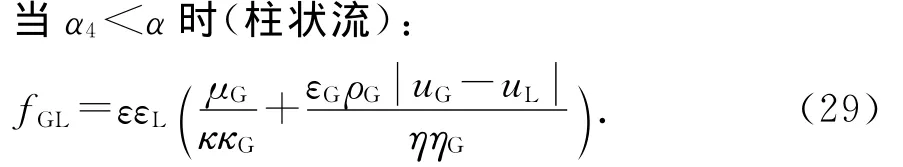
式中:κG和ηG采用公式(9)计算.
1.5.2 Schulenberg模型
Schulenberg基于两相流的动量方程研究多孔介质内气液流动,综合考虑气液间的虚拟质量力,毛细力,粘性力与惯性力对曳力影响,提出气固、液固和气液曳力模型[5].其气固、液固和气液间动量交换系数分别为式(30),式(33)和式(35).
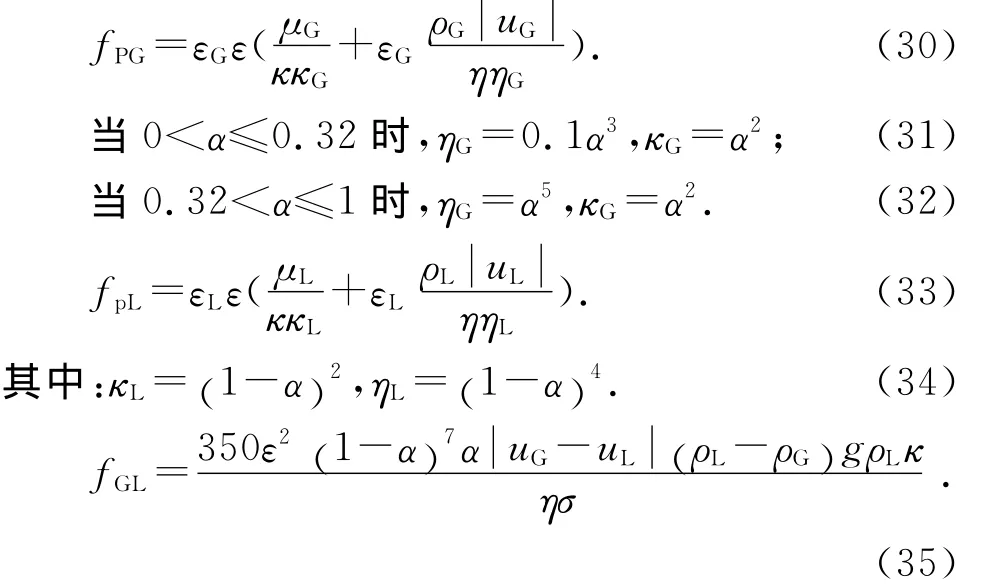
1.5.3 Attou双流体界面模型
Attou忽略层流粘性应力张量,用面积平均法建立稳态滴滤池一维气液两相数学模型,提出气固、液固和气液曳力模型[8].气固、液固和气液间动量交换系数为:
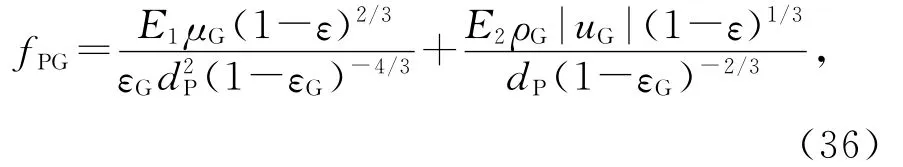
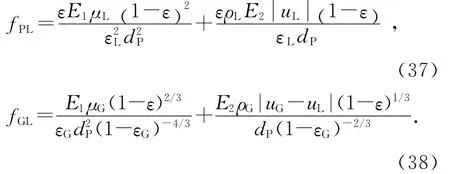
2 模拟对象与边界条件
2.1 模拟对象
试验装置如图1(a)所示.采用内径为50 mm,长度为1 m的有机玻璃管,竖直固定放置,管中分别填充直径为2,5,8 mm的玻璃球,测压环之间的距离为700 mm,气体(空气)与液体(去离子水)经气液混合器从下面流入球形多孔介质球床,从装置上端流出.气体与液体流量通过流量计测量,测压环的压强通过差压变送器测得,液体质量流量为36~324 kg/h,气体质量流量为0.05~13 kg/h[9].
本文的模拟对装置进行合理简化,反应器形状、尺寸如图1(b)所示.模拟计算区域为:测压环之间距离700 mm的试验段,其流体物质属性与实测值相同.利用ICEM对计算区域进行三维网格划分,网格类型为0型网格,网格单元总数为30 720个.
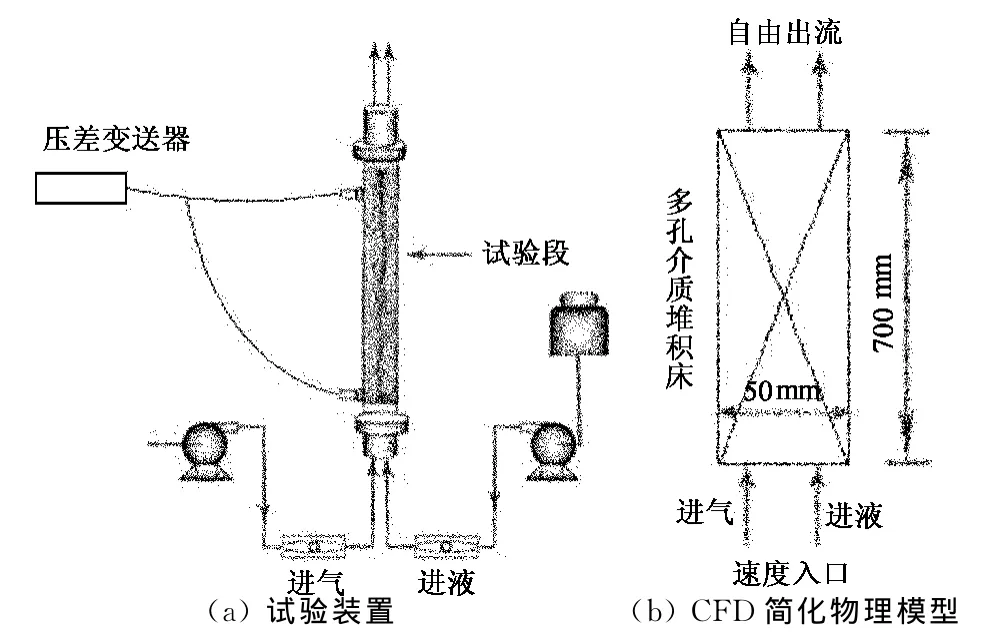
图1 试验装置与CFD物理模型Fig.1 Diagram of experiment and CFD physical model
2.2 模型设置
选用Fluent 6.3软件中多相流模型,即气液固三相欧拉模型,气体为连续相phase1,液体为phase2,球形多孔介质为静止相phase3,气相、液相和多孔介质三相间的动量交换系数通过编写用户自定义功能(UDF)添加到程序中.采用压力基非稳态求解器,时间步长为0.01 s,方程离散格式为一阶迎风格式,压力和速度的耦合采用simple算法,质量残差设定为5×10-4,其他残差设置为2×10-6.
2.3 初始条件和边界条件
反应器入口为速度入口,按照实验进口处测定气相与液相的质量流量分别转化为对应的速度,设定液相入口的体积分数,出口均为自由出流边界条件,壁面采用无滑移边界条件.
3 计算结果分析
3.1 阻力压降
影响气液两相流过多孔介质压降的因素有很多,如多孔介质颗粒的粒径、气液两相的流量、流体的属性和孔隙率的大小等众多因素.本文基于Tung &Siefken模型、Schulenberg模型以及Attou模型,利用CFD数值模拟方法,研究了气液流量、孔隙率和球形多孔介质粒径对阻力压降的影响,结果如图2,图3和图4所示.
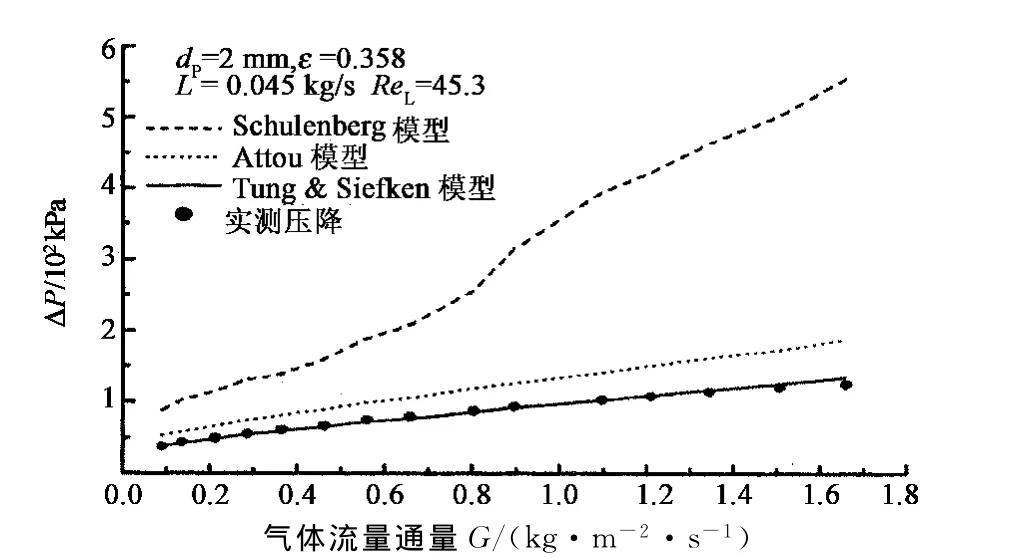
图2 进液量为0.045 kg/s的2 mm球床各模型压降与试验数据对比Fig.2 Comparison between pressure-drop models and experimental results(dp=2mm,L=0.045 kg/s)
从图2~图4可知,当固定进液流量,进气流量较小时,阻力压降增加较缓慢;当进气量逐渐增大时,阻力压降增加较快,这主要是由于阻力压降包括粘性力分量和惯性力分量,粘性力与速度成比例变化关系,惯性力与速度的平方成比例变化关系所致[10].当进气流速较小时,气相的雷诺数较小,粘性力分量所占份额较大,从而阻力压降增加较缓慢.随着进气流速增加,其雷诺数较高,气相的惯性力所占份额较大,导致气体与多孔介质边壁、气液间的作用力越来越大,并且较高的气相雷诺数推动同向的液体流动[3],从而导致阻力压降增加较快.
通过模拟和试验均发现,同样的气体和液体流量,颗粒越小阻力越大,这主要由于颗粒越小,其孔隙率越小,气液两相流在多孔介质内的真实物理速度越大,从而导致气体与多孔介质边壁、液体与多孔介质边壁以及气液间的作用剧烈.
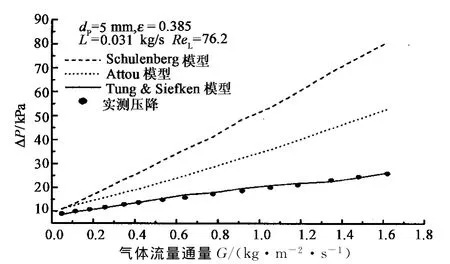
图3 进液量为0.031 kg/s的5 mm球床各模型压降与试验数据对比Fig.3 Comparison between pressure-drop models and experimental results(dp=5 mm,L=0.031 kg/s)
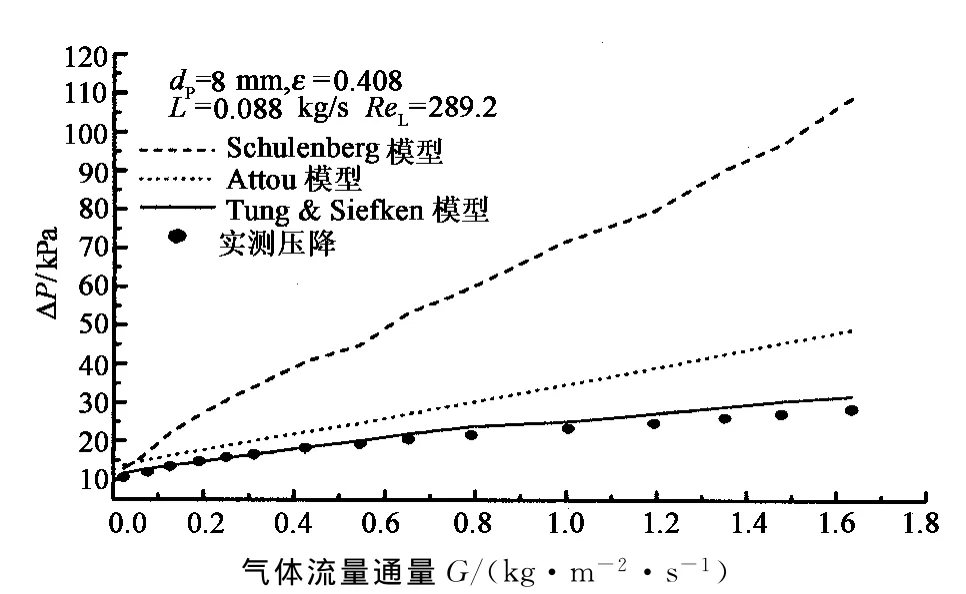
图4 进液量为0.088 kg/s的8 mm球床各模型压降与试验数据对比Fig.4 Comparison between pressure-drop models and experimental results(dp=8 mm,L=0.088 kg/s)
通过图2,图3和图4发现,Schulenberg模型模拟值均远大于实测值,原因可能是:其模型主要应用于高温高压下核反应堆多孔介质内气液两相流动,其计算的液体相对通过率远小于其他模型的相对渗透率[2],导致计算的液相惯性力较大,从而使模拟值远大于常温常压下的实测值.
Attou模拟值均比实测值偏大,其原因可能是:Attou模型是基于环状流流态基础上建立的双流体界面数学模型,主要应用于滴滤池内气液两相向下流动[8],其模型应用于多孔介质内非柱状流动还值得商榷.通过数值模拟发现,基于Attou模型不适合应用于多孔介质内气液两相同向向上流动.
在常温常压下滤料直径在2~8 mm的多孔介质床内气液两相流流动中,利用Tung &Siefken模型数值模拟压降值均与实测结果吻合很好,其主要原因可能是:Tung &Siefken模型考虑了泡状流,泡状-弹状流混合流,弹状流,弹状-环状混合流以及环状流不同的流型,并建立对应的曳力计算公式.
图5为利用Tung &Siefken模型多孔介质滤料粒径为8 mm,ReL为272.8,ReG为605.6数值模拟压降沿装置轴面变化云图.通过模拟可知,压降沿着流动方向均匀降低,且与实测压降数据较好吻合.

图5 dp=8 mm,ReL=272.8,ReG=605.6轴面压降云图Fig.5 The contours of pressure-drop changes along axial plane(dp=8 mm,ReL=272.8,ReG=605.6)
图6为采用Tung &Siefken模型液体质量流量为36~324 kg/h,气体质量流量为0.05~13 kg/h,进行CFD数值模拟值与实测值的关系图,并采用如下统计公式进行误差分析:
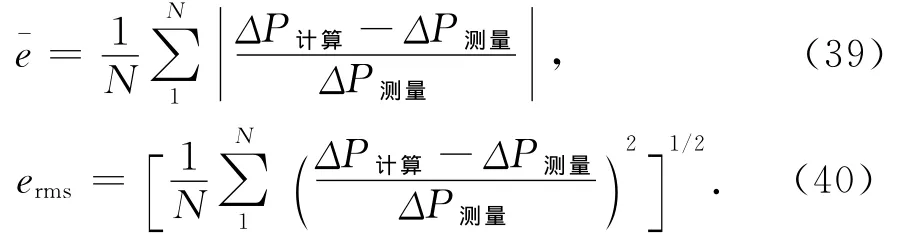
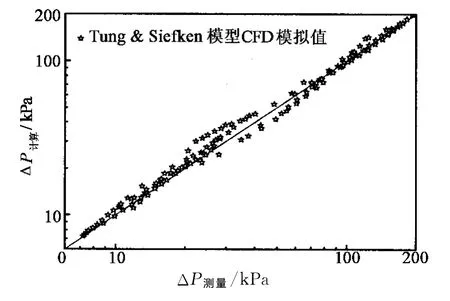
图6 Tung &Siefken模型CFD模拟压降值与实测值对比Fig.6 Comparison of pressure-drop based on Tung &Siefken CFD simulation with experimental results
平均相对误差ē为7.3%和相对误差的均方根erms为10.2%,通过图6与误差统计分析均得出:Tung &Siefken的模型能较准确数值模拟粒径为2~8 mm的多孔介质球床内气液两相流的压降.
3.2 持液量
持液量为多孔介质空隙内液体相的体积分数,不同的进气量和进液量以及孔隙率直接影响持液量值.图7显示了在液体流量为0.065 kg/s时,基于Tung &Siefken模型的CFD模拟持液量值随进气量与颗粒直径的变化情况.
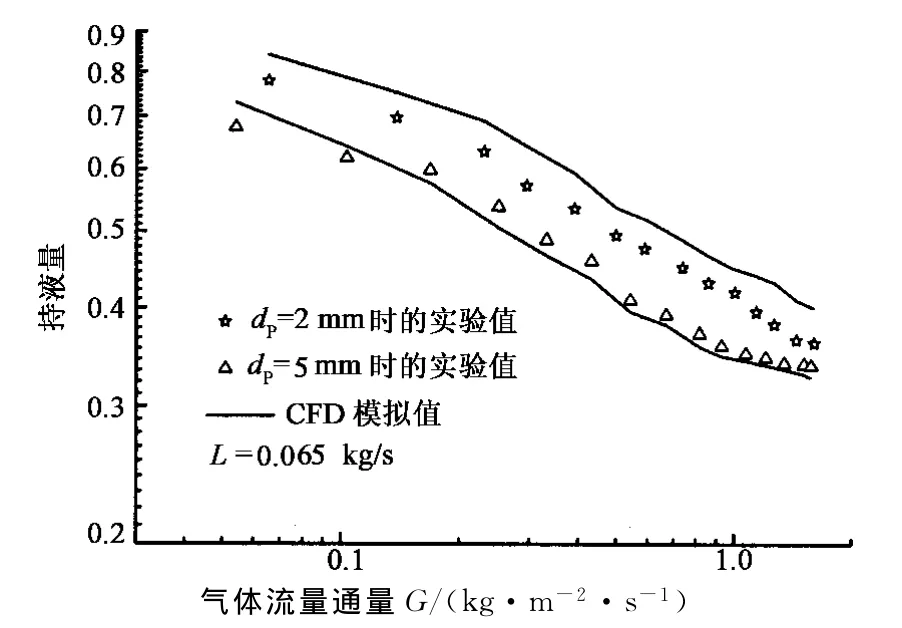
图7 进液量为0.065 kg/s的CFD数值模拟持液量与试验数据对比Fig.7 Comparison of liquid holdups using CFD simulation with experimental results(L=0.065 kg/s,dP=2 mm,dP=5 mm)
由图7可知,CFD数值计算持液量基本与实测数据一致,持液量随进气量的增加而逐渐降低.当粒径为2 mm时,液体持液量的CFD模拟值均大于实测值;当粒径为5 mm时,液体持液量的大多数CFD模拟值小于实测值.出现误差的原因是由于Tung&Siefken模型是在关于阻力压降实验的基础上总结的半经验模型,利用此模型计算出的持液量有一定误差,故需要通过大量实验对模型进行进一步完善.
4 结 论
在常温常压ReL=33~300,ReG=10~650内,本文基于Fluent计算流体力学软件中欧拉模型,分别采用Tung &Siefken模型、Schulenberg模型以及Attou模型,通过用户自定义功能编写气固、液固、气液间的曳力系数程序到软件中的形式,首次对球形多孔介质填充床内气液两相向上流动进行CFD三维数值模拟.通过模拟发现,Tung &Siefken模型更适合应用于粒径为2~8 mm的多孔介质球体内气液两相流的数值模拟,模拟压降值与实测值基本一致,平均相对误差为7.3%.CFD数值模拟的持液量与实测值变化基本一致,但是存在一定的误差.
[1] CHU W,DHIR V K,MARSHALL J.Study of pressure drop,void fraction and relative permeabilities of two phase flow through porous media[J].Heat Transfer-Seattle,AIChE Symposium series,1983,79:224-235.
[2] SCHULENBERG T,MULLER U.A refined model for the coolability of core debris with flow entry from the bottom[C]//Proceedings of the Sixth Information Exchange Meeting on Debris Coolability.Los Angeles,1984:1090-1097.
[3] TUNG V X,DHIR V K.A hydrodynamic model for twophase flow through porous media[J].International Journal of Multiphase Flow,1988,14:47-65.
[4] MOLGA E J,WESTERTERP K R.Gas-liquid interfacial area and holdup in a cocurrent upflow packed bed bubble column reactor at elevated pressures[J].Industrial &Engineering Chemistry Research,1997,36:622-631.
[5] SCHMIDT W.Interfacial drag of two-phase flow in porous media[J].International Journal of Multiphase Flow,2007,33:638-657.
[6] ERGUN S.Fluid flow through packed columns[J].Chemical Engineering Progress,1952,48:89-105.
[7] SIEFKEN L J,CORYELL E W.SCDAP/RELAP5 modeling of heat transfer and flow losses in lower head porous debris[R].Idaho Falls:Idaho National Laboratory,1999.
[8] ATTOU A,FERSCHNEIDERR G.A two-fluid hydrodynamic model for the transition between trickle and pulse flow in a cocurrent gas-liquid packed bed reactor[J].Chemical Engineering Science,2000,55:491-511.
[9] 李振鹏.球床多孔介质通道单相流体流动特性研究[D].哈尔滨:哈尔滨工程大学核科学与技术学院,2009.
LI Zhen-peng.Study on single phase flow in pebble-bed porous media channel[D].Harbin:College of Nuclear Science and Technology,Harbin Engineering University,2009.(In Chinese)
[10]廖永浩.微球床多孔介质通道气液两流特性研究[D].哈尔滨:哈尔滨工程大学核科学与技术学院,2009.
LIAO Yong-hao.Study on gas-1iquid two phase flow in microspheres bed porous media channel[D].Harbin:College of Nuclear Science and Technology,Harbin Engineering University,2009.(In Chinese)
CFD Simulation of Gas-liquid Two Phase Cocurrent Upflow through Porous Media
YU Jian1†,WANG Hong-tao1,2,LIAO Yong-hao3,GONG Guang-cai1
(1.College of Civil Engineering,Hunan Univ,Changsha,Hunan 410082,China;2.Army 91024,PLA,Taishan,Guangdong 529266,China;
3.Huadian Electric Power Research Institute,Hangzhou,Zhejiang 310030,China)
Based on computational fluid dynamics Euler multiphase model,gas-liquid two-phase co-current upflow through packed bed was investigated.Tung &Siefken model,Schulenberg model and Attou k-fluid model were applied,respectively.The gas-particle,liquid-particle and gas-liquid drag force programs were implemented to CFD three-dimensional numerical simulation with user defined functions.A comparison of the experiment data has shown that Tung &Siefken's model was more suitable for the numerical simulation of gas-liquid two-phase upflow through porous media packed with 2~8 mm sphere under normal temperature and pressure.The CFD numerical simulated values of pressure drop and liquid hold-up by Tung &Siefken's model were consistent with the experiment results.
Euler model;gas-liquid flow;porous materials;numerical simulation
X11
A
1674-2974(2012)08-0067-06*
2011-11-21
国家“十一五”水体污染控制与治理科技重大专项(2009ZX07423-004)
余 健(1964—),男,湖南益阳人,湖南大学教授,博士生导师
†通讯联系人,E-mail:jianyu@hnu.edu.cn
