库水位升降条件下不同渗透性的滑坡体稳定性变化规律

梁学战，陈洪凯

(重庆交通大学岩土工程研究所，重庆 400074)

0 引言

三峡水库在145～175m水位正常运营后，将有大量的边坡地质体在库水位周期性变化范围之内。实践表明，水库蓄水后库水位周期性涨落对边坡的失稳有显著作用，比如:Rasevelt湖1941年蓄水后，附近地区49%的滑坡发生在蓄水初期，30%发生在水位骤降时期;在日本，大约60%的水库滑坡发生在库水位骤降时期，40%发生在水位上升时期。针对库水位升降引起的边坡失稳问题国内外学者做了大量的研究［1-10］，刘新喜(2005)对红石包滑坡进行渗流数值模拟与稳定性研究表明，库水位下降使滑坡安全系数变化由大到小再增大的过程［8］。罗红明(2008)对三峡库区赵树岭滑坡进行了数值模拟，得出库水位上升时滑坡稳定系数总体逐渐增大，库水位下降时滑坡稳定系数总体逐渐减小［9］。刘才华(2005)认为库水位上升过程中，边坡的稳定性经历了一个先降低后增大的过程［10］。由此看出库水位升降对滑坡稳定性影响，对不同滑坡得出的结论不同，因此深入研究库水位周期性升降对滑坡稳定性影响有重要意义。

本文以长江三峡工程为背景，针对三峡库区水位的周期性调节对库岸边坡可能造成的影响，对具有不同渗透系数的滑坡体，采用饱和-非饱和数值模拟方法进行水库正常运营情况下滑坡体浸润线分布规律与稳定性变化规律的分析。

1 库水位升降对库岸边坡稳定性影响分析

库水位升降对库岸边坡稳定性的影响主要表现在以下两个方面:

(1)库水位升降对边坡岩土体物理力学性质的影响

水对岩土体强度是一个十分重要的影响因素。库水位升降过程中，含水量随之变化，岩土体尤其粘性土结构受到水的扰动，土粒间的胶结物质以及土粒、离子、水分子所组成的平衡体系受到破坏，土的强度降低、压缩性增大。水库蓄水上升过程中滑动面岩土体饱水软化，土体颗粒间的摩阻系数及粘结力减小，降低了坡体的抗滑力［11］。另外，库水位周期性升降，地下水渗流对坡体及滑面产生溶滤作用，坡体及滑面的矿物成分发生变化，从而影响岩土体的物理力学性质。

(2)库水位升降对边坡岩土体产生力学效应

当水库水位开始蓄水上升，水渗入滑体或滑面，滑面以上实压力体小于虚压力体，在滑体淹没部分就会产生浮托作用，这种浮托作用随浸润线位置变化影响整个滑坡体的稳定性。此外，库水位升降产生的渗透压力也是导致边坡稳定性变化的一个重要因素［12］，不同的渗透系数，库水位升降过程中的浸润线形状、岩土体饱水面积不同，产生的渗透压力对滑坡的稳定性影响亦不同。

2 库水位升降条件下不同渗透系数滑坡体饱和与非饱和浸润线分布规律

2.1 饱和－非饱和渗流计算基本理论

库水位升降作用下滑坡体内地下水浸润线的变化属于饱和与非饱和问题，浸润线是饱和土体与非饱和土体的分界线，在库水位涨落过程中，滑体内地下水浸润线也有规律的升降，饱和土与非饱和土的作用面积随之变化，因此根据质量守恒及达西定律可得到二维的饱和与非饱和渗流控制方程:

对于一个二维渗流分析模型，单元节点的厚度在整个网格中是常量，利用有限元方法，其方程的简介形式为:

非饱和渗流问题的边界条件有多种形式，本文研究的问题是库水位变化引起的滑坡体内暂态渗流场浸润线的变化情况，边界条件主要包含定水头边界及定流量边界两类。

2.2 计算模型

根据三峡库区云阳县凉水井土质滑坡地勘报告［13］，采取如图1所示的计算剖面和渗流计算模型，因只分析库水位升降作用下不同渗透系数滑坡体渗流场和稳定性变化的共有性质，所以滑坡模型得以简化，假定整个滑坡体及滑带为同一材料。所选滑坡坡面后缘高程约282m，前缘高程约110m，模型共划分3691个单元，3309个节点。边界:滑面为隔水边界即零流量边界，库水位以上为零流量边界;库水位以下为定水头边界;初始水头为145 m，做稳态渗流分析，分析结果为库水位运行中暂态分析的初始边界。计算步长在不同运行阶段均为3600s，步数根据不同运行阶段具体时间决定。

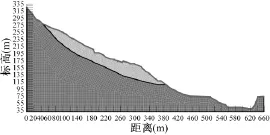
图1 渗流计算模型Fig.1 Calculation model of seepage

三峡水库的周期性运营状况直接影响库区滑坡的渗流场变化，本文按照三峡水库蓄水后正常运营时的水位调节方案(图2)，汛期6月中旬至9月底水库水位为145m。9月低至10月底蓄水至175m，库水位上升速率约1.0m/d，并在该水位持续运行180天，则库水位上升时定水头边界水头函数为:

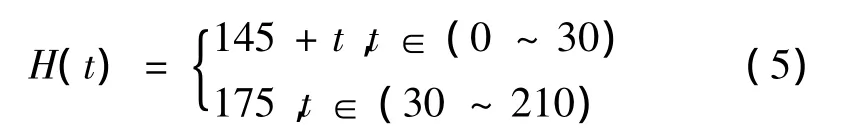
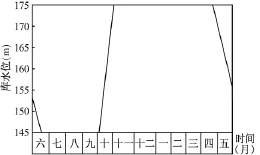
图2 三峡工程正常蓄水水库调度图Fig.2 Reservoir operation of normal water storage in Three Gorges Project

5月初至6月底，坝前水位从175m降至145m，平均约0.5m/d，此后保持在145m水位约90天，则库水位下降时定水头边界水头函数为:

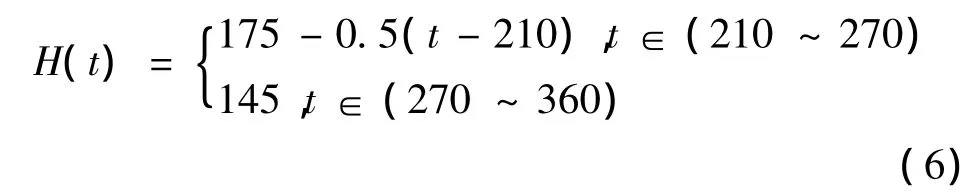
2.3 非饱和渗流计算参数

渗透系数可以表征土体导水能力，是影响库岸滑坡滑体渗流场的主要因素，在非饱和土渗流分析中，渗透系数是孔隙水压力的函数［14］。计算中选择代表三峡库区不同边坡土体材料4个数量级的饱和渗透系数(表1)，然后采用Geostudio软件Seep/W模块提供的不同岩土体材料标准试验参数，选取对应的基本土-水特征曲线进行库水位升降条件下滑体的渗流计算，得到不同渗透系数滑坡体在库水位升降时浸润线分布变化规律。

表1 计算选取的滑坡体饱和渗透系数Tabel 1 Saturated permeability coefficients of landslide for calculation

2.4 库水位升降不同渗透系数滑坡体浸润线分布特点及对滑坡的作用效应

库水位上升时地下水渗流特征，当渗透系数大于1×10-3强透水性时(图3a)，滑坡体内浸润线基本与库水位同步上升。渗透系数为1×10-4时(图3b)，滑坡体内浸润线变化稍滞后于库水位上升，表现出指向坡内的渗透压力。当渗透系数为1×10-5中等透水时(图3c)，滑坡体内浸润线明显滞后于水位上升，滑坡体内地下水出现“倒流”现象，指向滑坡体内的渗透压力增大，直到库水位保持在175m第150天后，滑面处的浸润线才到达175m。当渗透系数小于1×10-6弱透水时(图3d)，不仅库水位上升时浸润线有明显的滞后性，而且库水位在175m水位持续180天后，靠近滑面的浸润线仍存在滞后性，整个过程均表现出指向滑坡体内的渗透压力。在库水位上升过程中，地下水对滑坡体的浮托力始终是增大的，但增大的速率随渗透系数减小而变缓。

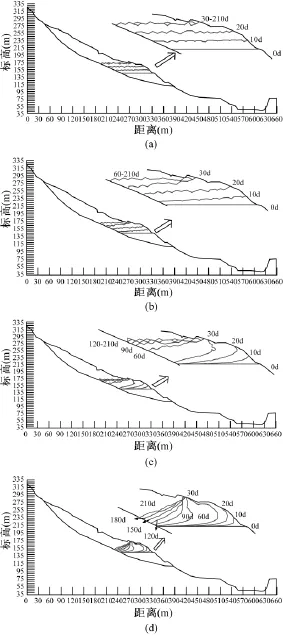
图3 库水位上升后滑坡体地下水浸润线Fig.3 Phreatic lines of landslide for the water level rise(a)—k=1×10-3m/s;(b)—k=1×10-4m/s;(c)—k=1×10-5m/s;(d)—k=1×10-6m/s

库水位下降时地下水渗流特征，当渗透系数大于1×10-3强透水性时(图4a)，滑坡体内浸润线基本与水位同步下降。当渗透系数为1×10-4强透水性时(图4b)，滑坡体内浸润线下降稍滞后于库水位，表现出指向坡外的渗透压力。当渗透系数为1×10-5中等透水时(图4c)，滑坡体内浸润线明显滞后于水位下降，滑坡体内地下水补给库水，指向滑坡体外的渗透压力增大，直到库水位保持在145m第360天后，滑面处的浸润线也未到达145m，说明整个过程均表现出指向滑坡体外的渗透压力;当渗透系数小于1×10-6时(图4d)，整条浸润线均存在明显的滞后性，整个过程不仅表现为指向滑坡体外的渗透压力，而且库水位在145m持续90天后，靠近坡面处的浸润线仍存在滞后性。在库水位下降过程中，地下水对滑坡体的浮托力始终是减小的，但减小的速率随渗透系数减小而变缓。

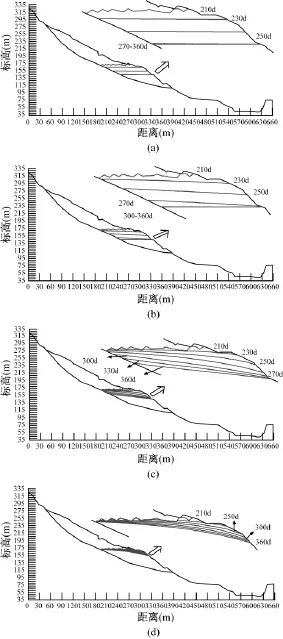
图4 库水位下降后滑坡体地下水浸润线Fig.4 Phreatic lines of landslide for the water level drawdown(a)—k=1×10-3m/s;(b)—k=1×10-4m/s;(c)—k=1×10-5m/s;(d)—k=1×10-6m/s

有以上分析看出，在相同的入渗条件下，饱和渗透系数对滑坡体浸润线有明显的影响。库水位上升阶段，浸润线总体为上升趋势，浮托力逐渐变大，但随着不同滑坡体渗透系数逐渐减小，靠近滑面的浸润线向上弯曲，浮托力增大的速度变缓，指向坡内的渗压逐渐增大;库水位下降阶段，浸润线总体为下降趋势，浮托力逐渐减小，但随着不同滑坡体渗透系数的逐渐减小，靠近滑面的浸润线向下弯曲，浮托力减小的速度变缓，指向坡外的渗压逐渐增大。

3 库水位升降条件下不同渗透系数滑坡体稳定性变化规律

3.1 稳定性计算理论

涉水土质滑坡稳定性分析不仅要考虑饱和区地下水压力变化影响，而且还应考虑非饱和区基质吸力变化影响，故采用Fredlund提出的考虑了负孔隙水压力的非饱和土抗剪强度理论［14］:

本例中用Morgenstern-Price法在考虑基质吸力情况下计算不同渗透系数库水位升降作用滑坡的稳定性变化。运用Geostudio软件，将Seep/W中的有限元网格导入到Slope/W中，用Slope/W的设置功能将Seep/W中的有限元水头值转换到Slope/W中，然后用地勘资料确定滑面，软件确定土体的条分数目并找出各土条的底面中心点，利用 Seep/W传递给Slope/W节点水头信息，Slope/W找到各土条底面中点在其单元中的相对坐标及其相应的插值函数矩阵，从而计算出底面中心点处的水头值，即:

由此，把动态的渗流场与极限平衡分析结合起来，模型的物理力学参数见表2。

表2 滑坡计算物理力学参数表Table 2 Calculation parameters of soil in landslide

3.2 库水位升降条件下不同渗透系数滑坡体稳定性变化规律

在库水位上升阶段，当渗透系数大于1×10-3时(图5a)，由于浮托力作用明显，稳定系数逐渐减小，水位在175m时保持不变。渗透系数为1×10-4时(图5b)，稳定系数水位上升期变大，水位在175m时先减小后保持不变，且稳定后的稳定系数小于起始条件145m时的稳定系数，主要原因是库水上升阶段指向坡内的渗透压力作用大于浮托力，到达175m水位后，浸润线保持水平，指向坡内的渗压消失，浮托力变大。渗透系数为1×10-5时(图5c)，稳定系数在水位上升时变大，水位在175m时先减小后保持不变，且变大和减小的幅度比1×10-4大，原因是此时产生指向坡内的渗压更大。渗透系数小于1×10-6时(图5d)，稳定系数在库水位上升期变大，水位在175m水位时一直减小，但水位在175m的最后第210天稳定系数仍大于初始条件145m的稳定系数，原因是指向坡内的渗压仍然存在，且浮托力变大的速率变缓。

在库水位下降阶段，当渗透系数大于1×10-3时(图5a)，由于浮托力一直减小，稳定系数除刚开始减小外一直增大，水位在145m时，稳定系数保持不变，且基本恢复到初始条件下的稳定系数。当渗透系数为1×10-4时(图5b)，稳定系数先减小后增大，主要原因是开始时指向坡外的渗压增大，此后浮托力继续减小，其作用大于渗压;在145m水位时指向坡外的渗压先减小后保持不变，稳定系数相应的先增大后保持不变。渗透系数为1×10-5时一直保持指向坡外的较大渗压，稳定系数一直减小(图5c);保持在145m时，指向坡外的渗压逐渐降低，浮托力亦减小，稳定性变大。渗透系数小于1×10-6时(图5d)与1×10-5稳定性变化规律基本相同，但是水位下降时稳定性系数下降幅度较大，水位在145m时稳定系数上升幅度较小，且水位在145m的最后第360天稳定系数远小于初始条件145m的稳定系数;原因是渗透系数小，虽然浮托力一直在减小，但减小的速率变缓，且一直保持指向坡外的渗透压力。

由此看出，在相同的入渗条件下，滑坡体稳定性的变化与不同渗透系数滑坡体在库水位正常运营过程中因浸润线形状变化产生的渗透压力与浮托力变化程度密切相关。

4 结论

库水位升降是影响库岸边坡稳定性的一个重要因素，本文通过理论分析和数值模拟方法得出以下结论:

(1)库水位升降对库岸边坡稳定性的影响主要表现在两个方面:一是库水位升降对边坡岩土体物理力学性质的影响，二是库水位升降对边坡岩土体产生浮托力和渗透力等力学效应。

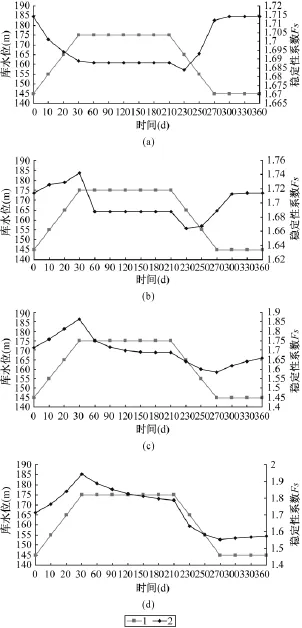
图5 稳定系数随库水位升降变化曲线Fig.5 Stability coefficient curve with reservoir water level fluctuation1—库水位;2—稳定性系数(a)—k=1×10-3m/s;(b)—k=1×10-4m/s;(c)—k=1×10-5m/s;(d)—k=1×10-6m/s

(2)三峡水库在正常运营时不同渗透系数滑坡体浸润线的变化规律不同。库水位上升阶段，浸润线总体为上升趋势，但是随着滑坡体渗透系数减小，靠近滑面的浸润线向上弯曲。库水位下降阶段，浸润线总体为下降趋势，但随着滑坡体渗透系数的减小，靠近滑面的浸润线向下弯曲。

(3)库水位升降过程中滑坡体稳定性的变化与滑坡体渗透系数大小密切相关。库水位上升阶段，渗透系数大于1×10-3时，稳定系数逐渐减小，在175m水位时保持不变;渗透系数为1×10-4时，稳定系数逐渐变大，在175m水位先减小后保持不变;渗透系数为1×10-5时，稳定系数与1×10-4时变化规律基本相同，但变大和减小的幅度较大;渗透系数小于1×10-6时，稳定系数逐渐变大，在175m水位时一直减小。在库水位下降阶段，渗透系数大于1×10-3时，稳定系数除刚开始减小外一直增大，在145m水位时保持不变;渗透系数为1×10-4时，稳定系数先减小后增大，在145m水位时先增大后保持不变;渗透系数为1×10-5时，稳定系数一直减小，在145m水位时一直变大;渗透系数小于1×10-6时与1×10-5稳定性变化规律基本相同，但稳定系数减小幅度较大，水位保持在145m时稳定系数变大幅度较小。

［1］Lane P A，Griffiths D V.Assessment of stability of slopes under drawdown conditions［J］.Journal of Geotechnical and Geoenvironmental Engineering，2000，126(5):443-450.

［2］李晓，张年学，廖秋林，等.库水位涨落与降雨联合作用下滑坡地下水动力场分析［J］.岩石力学与工程学报，2004，23(21):3714-3720.LI Xiao，ZHANG Nianxue，LIAO Qiulin，et al.Analysis on hydrodynamic field influenced by combination of rainfall and reservoir level fluctuation ［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(21):3714-3720.

［3］Jia G W，Zhan Tony L T，Chen Y M，et al.Performance of alarge-scale slope model subjected to rising and lowering water levels［J］.Engineering Geology，2009，106:92-103.

［4］Berilgen M M.Investigation of stability of slopes under drawdown conditions［J］.Computers and Geotechincs，2007，34(2):81-91.

［5］彭令，牛瑞卿.三峡库区白家包滑坡变形特征与影响因素分析［J］.中国地质灾害与防治学报，2011，22(4):1-7.PENG Ling，NIU Ruiqing.Analysisondeformation characteristics and influential factors of Baijiabao landslide in the Three Gorges Reservoir area［J］.The Chinese Journal of Geological Hazard and Control，2011，22(4):1-7.

［6］陈韶光，柳群义.水位涨落对库岸滑坡孔隙水压力影响的非饱和渗流分析［J］.公路工程，2008，33(6):55-71.CHEN Shaoguang，LIU Qunyi.The unsaturated seepage analysis for the influence of water level fluctuation to the pore water pressure of landslide in reservoir area［J］.Highway Engineering，2008，33(6):55-71.

［7］徐文杰，王立朝，胡瑞林.库水位升降作用下大型土石混合体边坡流-固耦合特性及其稳定性分析［J］.岩石力学与工程学报，2009，28(7):1491-1498.XU Wenjie，WANG Lichao，HU Ruilin.Fluid-solid coupling characteristics and atability analysis of soil-rocd mixture slope in rising and drawdown of reservoir water level［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28(7):1491-1498.

［8］刘新喜，夏元友，张显书，等.库水位下降对滑坡稳定性的影响［J］.岩石力学与工程学报，2005，24(8):1439-1444.LIU Xinxi，XIA Yuanyou，ZHANG Xianshu，et al.Effects of drawdown of reservoir water level on landslide stability［J］. Chinese Journal of Rock Mechanics and Engineering，2005，24(8):1439-1444.

［9］罗红明，唐辉明，章广成，等.库水位涨落对库岸滑坡稳定性的影响［J］.地球科学——中国地质大学学报，2008，33(5):687-692.LUO Hongming，TANG Huiming，ZHANG Guangcheng，et al.The influence of water level fluctuation on the bank landslide stability［J］.Earth Science —Journal of China University of Geosciences，2008，33(5):687-692.

［10］刘才华，陈从新，冯夏庭.库水位上升诱发边坡失稳机理研究［J］.岩土力学，2005，26(5):769-773.LIU Caihua，CHEN Congxin，FENG Xiating.Study on mechanism of slope instability due to reservoir water level rise［J］.Roch and Soil Mechanics，2005，26(5):769-773.

［11］陈洪凯，翁其能，袁建议，等.重庆库区典型松散土体的岩土力学参数敏感性试验分析［J］.重庆大学学报(自然科学版)，2000，23:203-206.CHEN Hongkai，WENG Qineng，YUAN Jianyi，et al.Sensitivity analysis of geotechnical physical and mechanics parameters tothetypicalloose earth in Chongqing reservoir［J］.Journa of Chongqing University(Natual Science Editon)，2000，23:203-206.

［12］王学武.三峡库区水位升降作用对库岸边坡影响研究［D］.成都:成都理工大学，2005.WANG Xuewu.Research on the effect to the bank slope in inpounding and drawdown of Three Gorges Reservoir water level［D］.Chengdu:Chengdu Unicersity of Technology，2005.

［13］重庆市高新岩土工程勘察设计院.重庆市云阳县故陵镇凉水井滑坡应急勘查报告［R］.重庆:重庆市高新岩土工程勘察设计院，2009.Chongqing High-tech Geotechnical Engineering Investigation and Design Institute. Emergency reconnaissance report of Liangshuijing in Guling town，Yunyang county，Chongqing city ［R］.Chongqing:Chongqing High-tech Geotechnical Engineering Investigation and Design Institute，2009.

［14］Fredlund D.G，H.Rahardjo.非饱和土力学［M］.陈仲颐译.北京:中国建筑工业出版社，1997.Fredlund D G，Rahardjo H.Unsaturated Soil Mechanics［M］.Translated by Chen Zhongyi.Beijing:China Architecture and Building Press，1997.