高超声速飞行器再入多段导引方法研究
2012-03-03刘冠南周浩陈万春
刘冠南,周浩,陈万春
(北京航空航天大学宇航学院,北京 100191)
引言
通用航空飞行器(Common Aero Vehicles,CAV)再入受到严格的过程和终端状态约束,设计一条使得飞行器满足各种过程和目标要求的弹道对制导方法有很高的要求[1-3]。文献[4]提出了一种满足过程约束和终端条件的纵向参考轨迹的在线生成方法;文献[5]基于此引入了过渡段对可重复使用运载器X33进行再入仿真;文献[6]采用速度方向与视线方向偏差角走廊进行了横程控制。本文在这些基础上提出多段弹道的导引律,将再入轨迹分为初始下降段、过渡段和占大部分飞行时间的拟平衡滑翔段,在初始下降段和过渡段,利用拟平衡滑翔条件(Quasi-Equilibrium Glide Condition,QEGC)把约束转换为倾侧角的上界,通过限制倾侧角的大小来满足约束,在地面生成参考弹道;拟平衡滑翔段采用纵向和横向分开制导的预测校正方法,纵向制导算法用于决定倾侧角的大小,横向制导决定倾侧角的方向,在机载计算机上实时预报实际落点和目标落点的偏差,计算控制信号,调节倾侧角的大小和方法,消除偏差。
1 CAV再入动力学建模
以CAV-H[7]为对象,考虑地球自转,建立飞行器三自由度质心运动模型。
1.1 三自由度质心运动方程
无量纲化的三自由度质心运动方程如下:


式中,m为飞行器质量;ρ为大气密度,通过Matlab函数atmoscoesa得到;Sref为参考面积;H为飞行器高度;R0为地球半径;阻力系数CD和升力系数CL的表达式[7]如下:
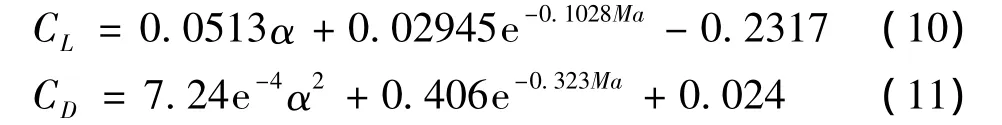
从防热的角度考虑,迎角α由其随Ma的变化规律得出[6],那么方程中唯一的控制变量是倾侧角σ。
1.2 过程约束和终端约束
不同的再入阶段轨道约束不同,因为初始速度很大,初始下降段约束主要是热流密度。在再入中段,为保证飞行器的机动能力,过载成为了主要约束。在再入末段速度相对较小,此时为保证飞行器的可操作性,动压成为主要约束。此外,为了防止弹道大幅度振荡,需要考虑到平衡滑翔(EG)约束。将上述约束依次表达如下,这几种约束也可以转换到速度-高度坐标系形成一条再入走廊,如图1所示。

式中,kQ=1.0387×10-8;σEQ为平衡滑翔倾侧角。为了顺利转换到末端能量管理段并达到指定目标,需满足再入段末端约束:rf=rTE,Vf=VTE,Sf=STE,其中下标f表示最终状态,S表示飞行器当前位置到目标点的大圆弧距离。
为了保证飞行器的稳定性,要求倾侧角上、下限分别为 σul=80°,σll= -80°。

图1 CAV再入走廊
2 再入多段导引算法
本文采用纵向与横向分开制导的预测校正方法,纵向制导算法用于决定倾侧角的大小,横向制导确定倾侧角的方向[1]。每过一定时间以飞行器当前飞行状态作为初始值,生成一条参考弹道。然后控制导弹跟踪该参考弹道并通过倾侧角符号反转控制横向运动。
2.1 将轨道约束转换成倾侧角约束
2.1.1初始下降段最大允许倾侧角
为保证该段弹道不会超出热流密度约束,需要找到初始下降段常值倾侧角上限σinm。
代入一个常值倾侧角,积分式(1)~式(6)直到满足:

式中,δ为一个小量常数;下标QE表示平衡滑翔。式(17)表示当前点的斜率,通过式(1)与式(4)相除并略去地球自转影响得到。倾侧角为零时QEGC表达式为:
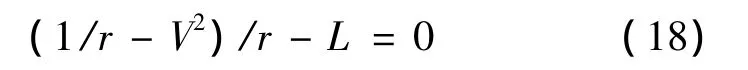
将上式中r看作V的函数,并取r相对V的导数,可得式(16)中的(dr/dV)QE:
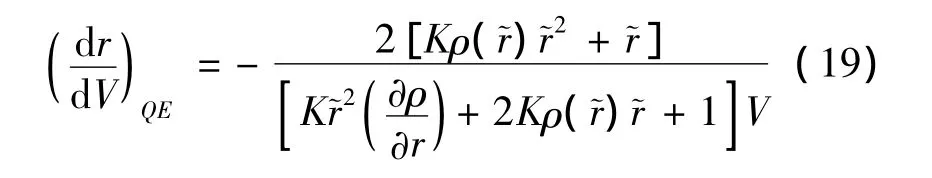
式中,K=R0SrefCL/(2m);~r为对一个给定V值,求解式(18)得到的r值。由文献[5]可知,随着初始下降段常值倾侧角的增加,对应的热流密度峰值变大。取初始下降段常值倾侧角σinm为下式取最大值时的倾侧角值:
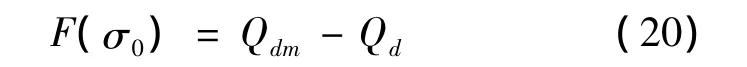
将满足式(16)和式(20)的弹道点称为转换点PT,该点速度称为VPT。
2.1.2过渡段的倾侧角范围
初始下降段结束后,采用常值倾侧角将导致弹道较大的振荡,因此采用约束上限σQEm(V)作为该段倾侧角,详见下节中的式(22),该段末速度没有严格的要求,0.8能很好地满足要求。
2.1.3准平衡滑翔状态下的倾侧角范围

轨迹约束式(12)~式(14)组成了再入走廊的下边界,再入弹道必须位于这条下边界之上,如图1所示。为此,将式(12)~式(14)看成空气密度关于速度的函数,对一个给定速度值,求得最大密度ρmax(V)就是这一速度下满足轨迹约束的空气密度上限,以此最大密度求得最大升力值Lmax(V),由式(21)得到:
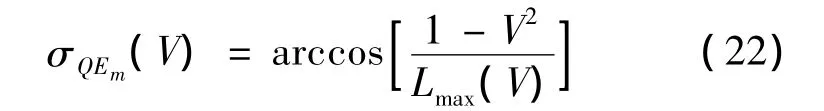
QEGC提供了求解满足所有约束的倾侧角范围的方法。如图2所示,对平衡滑翔段弹道的任意速度值,倾侧角范围为:

倾侧角控制律为:

BANK-SIGN(σ)详见后面的横向制导。

图2 平衡滑翔段弹道的倾侧角范围
2.2 纵向制导
倾侧角制导律迭代公式如下:
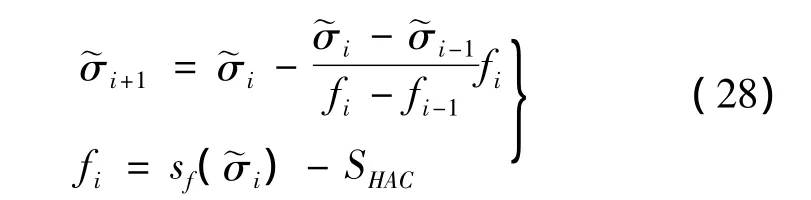
式中,fi为目标落点和预测落点之间的大圆弧度,即预测落点误差。首先给定初始倾侧角,积分运动方程,预测飞行器达到末端速度VTE时的fi值。将此fi值与要求值进行比较,若偏差满足精度要求,则迭代终止,若不满足,通过式(28)计算新的σ,继续上述过程。
2.3 横向制导
将速度方向和到目标的视线角的偏差记做ψΔ,倾侧角的符号应使得ψΔ逐步减小以满足末端要求。
倾侧角的方向是通过横向制导控制来实现的,首先建立横向制导的方向误差走廊[6](见图3)。当ψΔ超过方向误差边界,σ反向。若Δψ超出了该走廊,倾侧角方向由下式决定:
BANK-SIGN(σ)=-BANK-SIGN(σ)(29)
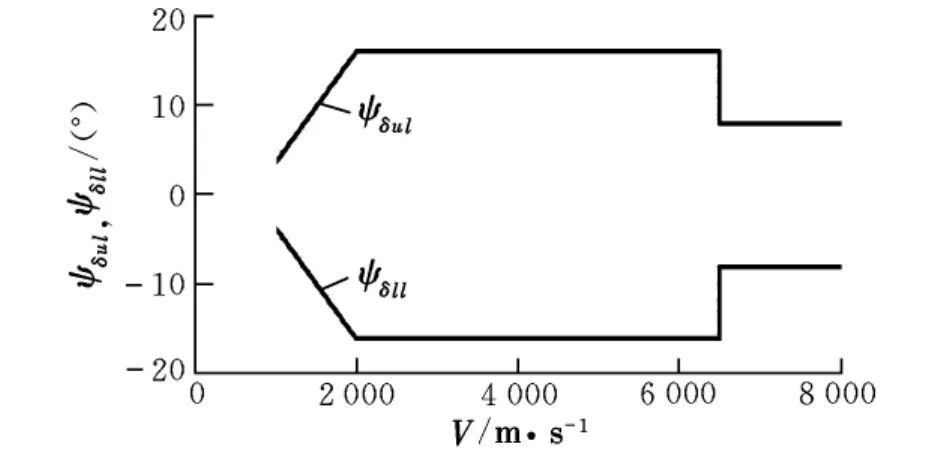
图3 方向误差走廊
3 数学仿真
以CAV-L飞行器作为数学仿真模型,对本文的方法进行数学仿真验证,飞行器质量m=816.48 kg,Sref=0.325 8 m2,每50 s更新一次参考弹道。实际弹道偏差为三种均值为零的Gaussian分布(见表1[1]),弹道初始再入状态和弹道约束如表 2、表 3所示。

表1 实际弹道偏差

表2 初始再入状态

表3 弹道约束
仿真得到Vf=1.5 km/s,Sf=23.5 km,满足末端精度要求。平衡滑翔段的弹道仿真结果见图4~图10。

图4 时间-倾侧角

图5 时间-方向偏差角

图6 速度-再入弹道

图7 时间-热流密度及其上限

图8 时间-动压及其上限
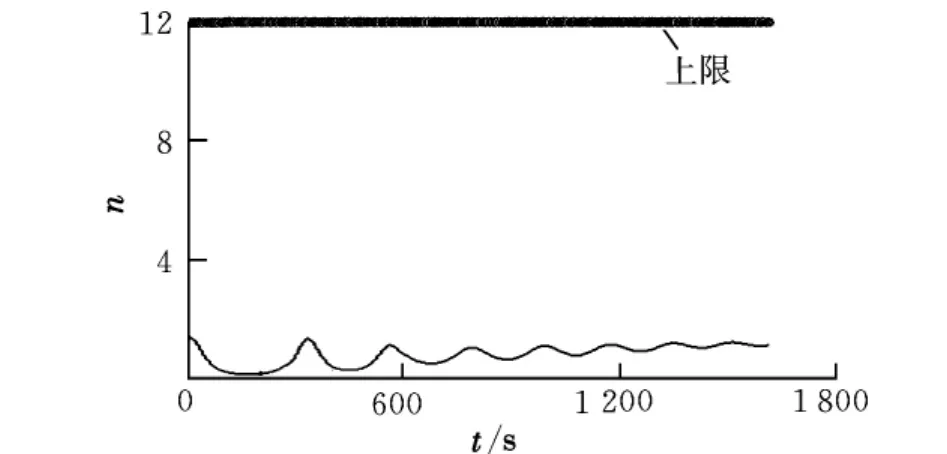
图9 时间-过载及其上限

图10 弹道经纬度曲线
由图4~图10可知,整条弹道没有大的振荡。倾侧角只需一次翻转,就可以实现对视线角偏差ψΔ的控制要求,在倾侧角翻转的同时,速度的视线偏差角的大小变化反向。弹道满足各种飞行过程约束的制导律,平衡滑翔段的弹道十分平稳,实际动压和过载离其对应的上限值有很大距离,弹道的经纬度曲线也比较平滑,本文采用的多段导引方法很好地满足了控制要求。
4 结束语
本文将再入轨迹分为初始下降段、过渡段和拟平衡滑翔段并分别设计制导律,快速地得到了满足过程约束和目标要求的弹道。过渡段的引入很好地解决了飞行器从初始再入段结束至平衡滑翔段开始之前的弹道上下剧烈振荡问题。利用拟平衡滑翔条件将再入过程约束转换成对侧倾角上限的约束,很好地满足了弹道的过程约束条件,并且不会带来大的计算量,不致影响参考弹道的在线实时生成。同时,在弹道实际飞行有一定偏差的情况下,纵向和横向分开制导的预测校正方法很好地控制飞行器到达目标落点。相对传统的轨迹设计与跟踪的再入制导方法,该方法既很好满足了各种约束,具备计算快速性,又能有效应对不确定因素的干扰,有进一步研究的潜力。
[1] 沈作军.航天器先进再入制导技术研究综述[C]//中国宇航学会首届学术会议论文集.北京:宇航出版社,2005:103-104.
[2] 赵汉元.飞行器再入动力学和制导[M].长沙:国防科学技术大学出版社,1997:382-412.
[3] 赵汉元.航天器再入制导方法综述[J].航天控制,1994,22(1):26-33.
[4] Shen Z J.On-board three-dimensional constrained entry flight trajectory generation[D].Iowa State of America:Iowa State University,2002.
[5] Xue S B.Constrained predictor-corrector entry guidance[R].AIAA-2009-5867,2009.
[6] Zhou W Y,Chen H B,Yang D.Entry guidance for common aero vehicle[C]//The 2nd International Symposium on Systems and Control in Aerospace and Astronautics.Shenzhen,2008:1-6.
[7] Duan G R,Sun Y,Zhang M R.Aerodynamic coefficients models of hypersonic vehicle based on aero database[C]//2010 First International Conference on Pervasive Computing,Signal Processing and Applications.Harbin,2010:1001-1004.
