无人直升机高精度位置控制

尹亮亮，黄一敏

(南京航空航天大学自动化学院，江苏南京 210016)

引言

无人直升机在有限平台(大厦停机坪、舰船甲板等)下进行自主着陆时，对位置控制精度有极高的要求。ADS-33直升机飞行品质规范中对位置控制精度也有明确的规定［1］。现代控制虽然能达到比传统控制更优越的性能［2-3］，但是其设计方法必须以准确的对象数学模型为依据，而直升机由于其复杂的动力学特性，难以建立准确的数学模型。因此，以物理概念为依据，不追求模型准确的控制方法是为当前无人直升机飞行控制所推崇的，PID控制器也正是因为这些特性在飞行控制领域得到了广泛的应用。

但是，常规的PID控制器由于控制功效的限制，难以满足复杂环境下进行高精度位置控制的需求，而非线性PID能弥补控制功效的不足。本文结合非线性PID的原理，并结合无人直升机位置控制的特殊性，设计了一种位置控制律，该控制律在位置偏差进入一定区域后，随着偏差的降低，控制增益提高，保证控制精度，同时相角超前增大，弥补因增益提高导致的相角裕度损失，保证稳定性。

1 无人直升机控制律介绍

1.1 无人直升机控制架构

无人直升机横纵向控制律架构如图1所示。位置控制律形式为:

式中，δele和δail的前三项为位置控制，后两项为姿态增稳;ΔX，ΔY为纵、横向位置偏差;ΔVx，ΔVy为纵、横向速度偏差;q，p为俯仰角速率和滚转角速率;θ，φ为俯仰角和滚转角;δele，δail为纵向周期变距和横向周期变距输出。

图1 无人直升机横纵向控制律架构

1.2 无人直升机高精度控制的难点

无人直升机自身动态特性及外界环境的影响决定其难以提高控制精度:

(1)小型无人直升机几乎都采用跷跷板式旋翼结构，操纵力矩全部来自于旋翼升力，而直升机在悬停状态下，旋翼气动焦点距离重心较近，操纵效率非常低下［4］;

(2)直升机在悬停条件下，受到严重的气流扰动，而小型无人直升机由于重量轻，对风非常敏感。

图2给出了实际的试飞结果，可以看出位置偏差一直处于大幅飘动状态，这就是气流扰动的结果，该控制精度远不能满足有限平台着陆的需求。

在常规控制下，为了提高控制精度，一般可采用两种方法:

(1)引入积分控制。积分项能起到消除稳态误差的作用，当无人直升机处于稳定风场下时，积分项确实能提高控制精度。通过大量的试飞发现，无人直升机在飞行过程中，其气动环境非常复杂，尤其在山区等复杂地形上空飞行时，风场时刻都处于变化之中，难以预测，在这种情况下，积分控制对精度的提高并不明显，图2的试飞结果也如实地印证了这一结论。

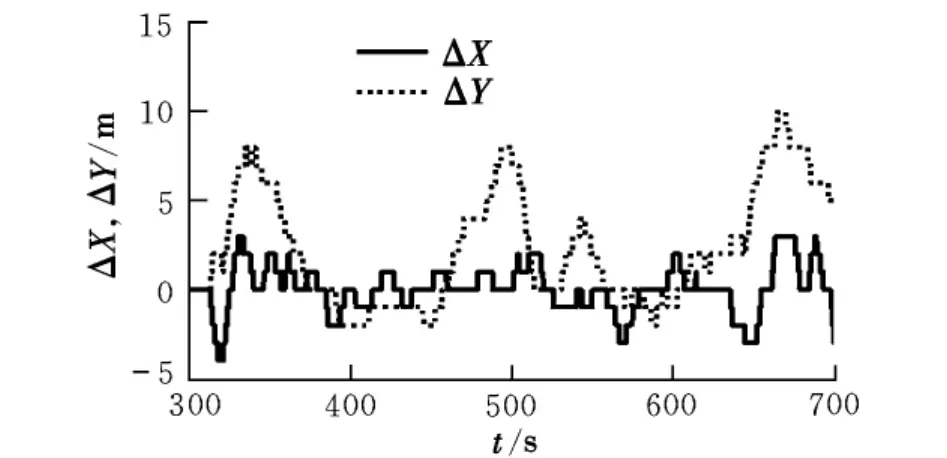
图2 无人直升机在变化风场下的位置偏差

(2)采用高增益控制。控制偏差和控制增益是成反比的，因而，提高控制增益可从一定程度上改善控制精度。如 Boeing公司和 Ames Research就在UH60直升机上实现了高增益控制［5-6］，使位置保持精度达到一级飞行品质要求。但是高增益控制会使系统带宽整体提高，这样必须对之前不太关心的执行机构和旋翼等高频部件进行准确的建模。而且高增益控制对传感器精度、信号品质、执行机构带宽、采样频率和飞控计算机延迟都有更为严格的要求，工程实现非常困难。

为此，本文提出了一种非常规的控制策略，即非线性反馈PID控制器，并针对无人直升机位置控制的特点进行改进，以提高无人直升机位置控制精度。

2 非线性反馈PID

非线性反馈PID控制器的一般形式［7］为:

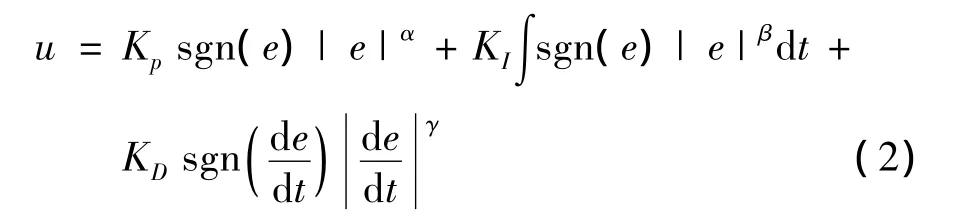
与常规控制不同，非线性反馈PID以误差信号的分数阶作为反馈信号，这样，控制器除了3个基本参数KP，KI，KD外，还可以通过非线性因子 α，β，γ改变反馈信号的非线性特性，以达到更好的控制性能。而常规PID控制器是非线性反馈PID控制器在α=β=γ=1时的特殊形式。

非线性反馈PID控制器具有以下优点:

(1)非线性反馈PID是常规PID控制器的推广，因而，前者也具有后者的一些特点，如鲁棒性好和对模型需求低等;

(2)与传统PID相比，能达到更好的控制性能;

(3)物理意义明确，非线性反馈的实质是根据偏差大小动态优化控制增益，每个参数的作用都很有针对性;

(4)工程易实现，非线性反馈PID的架构和常规PID是完全一致的，由常规PID控制器升级到非线性反馈PID控制器，要进行的工作仅仅是对误差信号进行分数阶处理，而这在计算机控制系统中是非常容易实现的。

但是非线性反馈PID在带来诸多优点的同时，也给控制器调参增加了难度。本文对一般形式的非线性反馈PID进行了改进，使调参得到一定程度的简化。

3 无人直升机高精度位置控制

3.1 高精度位置控制策略

本文在非线性反馈PID的基础上，结合无人直升机位置控制的特点，设计了一种高精度位置控制策略。

高精度位置控制策略只针对位置控制回路，增稳回路保持不变，为了表述方便，文中以uout表示外回路的位置控制器输出。由于横向通道与纵向通道控制策略相同，这里只给出纵向通道高精度位置控制策略的表达式:

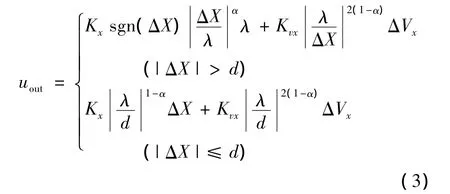
式中，α为非线性因子，0＜α＜1;λ为非线性边界;d为线性饱和区域。该控制律具有以下特点:

(1)λ为常规位置控制策略和高精度控制位置控制策略的分界点，λ一方面影响控制器的调节效果，另一方面也是对飞行安全的保障，即使高精度控制出现不稳定，位置偏差变大，当超出非线性边界后，仍可切换为常规控制。

(2)α为(0，1)之间的数值，当位置偏差进入非线性边界后，控制器增益会随着位置偏差的降低而增大，提高控制精度。

(3)当d≤|ΔX|＜λ时，微分项增益随比例项同步变化，而不同于式(2)形式的控制律，比例项和微分项是独立的。式(2)控制律的好处是可以通过提高速度的控制精度而保证位置控制的跟踪性能，但是，容易诱发振荡。而无人直升机在着陆阶段为位置保持模式，对跟踪性能没有要求。式(3)的控制律传递函数为:

可以看出，控制律随位置偏差降低，增益增大的同时，相角超前也增大，这样可以补偿系统因增益提高而带来的相角裕度损失，以保证稳定性。同时，由于控制律不需要确定微分项非线性因子，也降低了调参的困难。

(4)不使用积分项，由于高精度控制律已能满足精度需求，再使用积分项对精度的提高并不明显，而积分项的引入是以牺牲系统带宽和稳定性为代价的。

(5)线性饱和区域d的引入是为了提高系统在过零点区域的动态性能，控制律在过零点区域会因增益过大而产生抖动，虽然这种抖动是区域性的，不影响全局的稳定性，但是会降低舵机的使用寿命。

图3为完整的位置控制示意图，当位置偏差大于非线性边界时，采用常规的位置控制策略;当进入非线性边界范围后，切换为非线性反馈控制，此时，控制增益随位置偏差的降低而升高，提高控制精度;随着位置偏差的进一步减低，进入线性饱和区域，控制增益不再升高，防止舵机抖动。

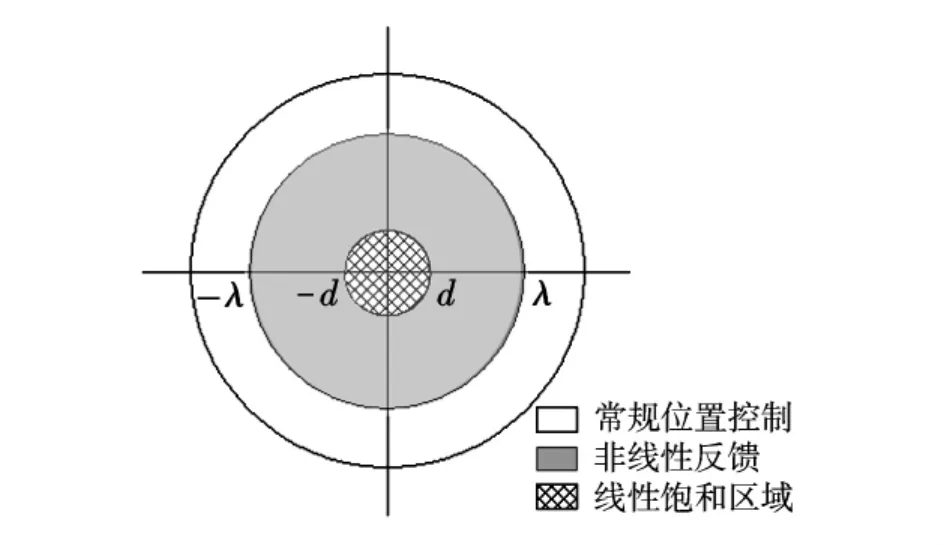
图3 高精度位置控制策略示意图

3.2 精度分析

同等扰动下，常规控制律误差为enor，高精度控制律误差为epre，则具有如下关系:

则:

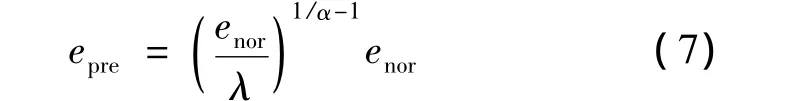
而 λ ＞enor，0＜ α ＜1，所以epre＜enor。说明高精度控制律控制精度高于传统控制律，而通过合理地选取λ和α，可使控制精度得到成倍提高。

3.3 参数整定

高精度控制律是建立在常规控制律基础之上的，因此，在设计控制律时也应遵循以下原则:先设计好常规控制律，再根据常规控制所能达到的精度和精度指标需求，进行高精度控制律的设计。

高精度控制律涉及到5个参数:Kx，Kvx，λ，α和d。其中Kx，Kvx是按照常规控制的方法进行确定的，本文不对此进行具体阐述;λ，α和d是与高精度控制相关的参数，而d的作用是对过零点区域的优化，不影响控制精度，设计初期可不用考虑。因此，高精度控制律参数整定主要是确定λ和α。

根据式(7)的结论，高精度控制律控制精度是λ和α的函数，λ越大，控制精度越高，α越小，控制精度越高。图4给出了控制律在不同λ和α组合下的对比结果。控制误差的对比如表1所示。

图4 不同参数对比结果

表1 控制误差对比

表1的结果和式(7)是吻合的，其中α=1时为常规控制律。而图4的对比结果表明，盲目地追求控制精度会导致控制品质的下降。一般建议λ/enor控制在(2，4)之间，α控制在(1/3，2/3)之间，可较好地处理好控制精度和控制品质的折中。

在确定λ和α后，增加线性饱和区域d可很好地改善过零点的动态性能，一般取d≈epre。

4 仿真分析

4.1 测试科目

为了验证无人直升机位置控制精度，本文设计了如下测试科目，整个测试科目分为3个阶段:

阶段1:由悬停点前方50 m飞行至悬停点;

阶段2:在悬停点处悬停保持;

阶段3:由悬停点处开始下降，进行自主着陆。

为了模拟无人直升机真实的飞行环境，在仿真过程中施加了幅值为5 m/s的扰动风，图5为测试科目的示意图，其中H为飞行高度。

图5 测试科目示意图

4.2 仿真结果分析

本文分别采用高精度位置控制和常规控制策略进行了上述飞行科目的仿真测试，高精度控制参数选择为:λ=15，α=1/2，d=1。仿真结果如图 6所示。

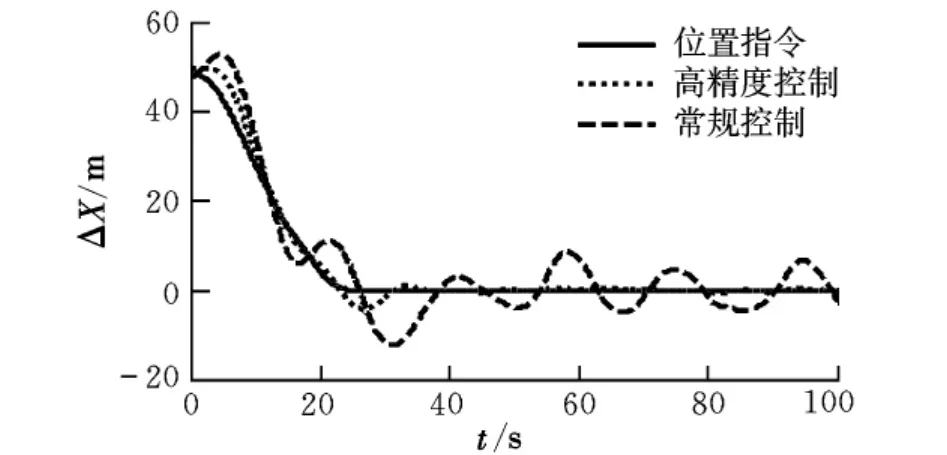
图6 位置控制仿真结果

从仿真结果可以看出，采用常规控制策略时，位置偏差达到了7 m，这是由于积分项不能适应动态扰动所致。而高精度位置控制律能较好地抑制动态扰动的影响，位置偏差仅为1 m左右，明显要好于常规的位置控制策略。而且，从阶段1位置跟踪的效果来看，高精度位置控制律也胜于常规控制策略。

5 结束语

本文将非线性反馈技术用于无人直升机位置控制中，提高了无人直升机在悬停状态下的抗扰动能力和位置控制精度，极大地改善了无人直升机进行自主着陆的安全性。非线性反馈根据控制偏差实时优化控制增益，使控制器不需要积分环节就能获得较高的控制精度，而且非线性反馈控制器的实施过程极为简单，容易在工程上进行推广使用。但是，非线性反馈控制器的稳定性目前仍难以用解析方式进行证明，这也是日后研究的重点。

［1］ Anonymous.AMCOM ADS-33E-PRF Aeronautical design standard，handling qualities requirements formilitary rotorcraft［S］.Huntsville，Alabama:U.S.Army Aviation and Missile Command，2000.

［2］ Tanner O，Geering H P.Position an autonomous helicopter with high accuracy using robust controllers［C］//AIAA Guidance，Navigation，and Control Conference and Exhibit.Montreal:AIAA，2001:1-17.

［3］ Shin J，Nonami K，Fujiwara D，et al.Model-based optimal attitude and positioning control of small-scale unmanned helicopter［J］.Robotica，2005，23(3):51-63.

［4］ Prouty RW.Helicopter performance，stability，and control［M］.Boston:Boston PWSEngineering，1986.

［5］ Mark B Tischler.Digital control of highly augmented combat rotorcraft［R］.Moffett Field，California:Aeroflightdynamics Directorate，U.S.Army Aviation Research and Technology Activity，Ames Research Center，1985.

［6］ Landis K H，Glusman S I.Development of ADOCS controllers and control laws［R］.Philadelphia:Boeing Vertol Company，1985.

［7］ 韩京清.自抗扰控制技术:估计补偿不确定因素的控制技术［M］.北京:国防工业出版社，2008.